The main result of this thesis is a method for writing programs with graphical user interfaces in purely functional languages. The method is based on a new abstraction called the fudget. The method makes good use of key abstraction powers of functional languages, such as higher order functions and parametric polymorphism.

The Fudget concept is defined in terms of the simpler concept of stream processors, which can be seen as a simple, but practically useful incarnation of the process concept. Programs based on fudgets and stream processors are networks of communicating processes that are built hierarchically, using combinators. Communication is type safe. The basic combinators provide serial compositions, parallel compositions, and loops. A key difference between previous work on stream processing functions and our approach is that we deliberately abstract away from the streams. We obtain a system that can be implemented deterministically, entirely within a purely functional language, but which also makes it possible to take advantage of parallel evaluation and indeterminism, where such is available within the functional language. The purely functional approach makes processes first class values and makes it easy to express process cloning and process migration.

The practical viability of the approach is demonstrated by the Fudget library, which is an implementation of a graphical user interface toolkit in the purely functional language Haskell, together with a number of small an large applications that have been implemented on top of the library.

In addition to GUI programming, fudgets are suitable for other forms of concurrent I/O programming. We demonstrate how client/server based applications can be we written, with type safe communication between client and server. We show a web browser as an example where GUI programming and network communication come together.

We view fudgets as one example of a more general combinator-based approach to promote the idea that a functional language together with combinator libraries is a good alternative to using less expressive languages propped by application-specific tools. We describe a set of combinators, reminiscent of parsing combinators, for building syntax-directed editors.

Preface

This monograph acts as theses for both authors. Most of the work behind has been carried out in close cooperation between the authors, but some chapters present work of a more individual nature:

Thomas Hallgren:: Chapters 19, 27, and 39. He has also developed the applications in Part V (some contributions are due to Magnus Carlsson in Chapters 36 and 37, though).
Magnus Carlsson:: Chapters 24, 25, 28, and 29.

Acknowledgements

We wish to thank Thomas Johnsson, Lennart and Jessica Augustsson, Johan Nordlander, Bengt Nordström, Niklas Röjemo, David Sands, Colin Runciman and Simon Peyton Jones for proofreading and numerous suggestions for improvements on drafts of the thesis. A special thanks to Ola Freijd, who has made all illustrations and the cover page.

Ideas and implementation work by a number of people have increased the usefulness of the Fudget library. Jan Sparud's space-leak fix in an early version suddenly made it possible to run fudget programs until somebody pulls the plug. Jan also implemented an initial version of the name layout mechanism. Lennart Augustsson's integration of the Xlib interface with HBC's runtime system made fudget programs easier to use and more efficient. John Hughes invented the default parameter simulation, which made fudget programming much more pleasant.

The department of Computing Science has not only provided a wealth of academic stimulus, but also technical and administrative support that has shown a flexibility of unusual quality. Especially, we want to thank Christer Carlsson, Görgen Olofsson, Marie Larsson, Per Lundgren, and Hasse Hellström.

Part of our work has been supported by NUTEK.

Historical reflections

Once upon a time on a gray autumn day in 1991, three functional programmers were chatting during a coffee break. They were quite happy that the LML compiler [AJ93] allowed them to write ``real'' programs in a pure functional language. One of these three had implemented a version of the game Tetris in LML. Another had implemented Worms; an interactive, multi-user, real-time game [Hal90]. They had no efficiency problems with these kinds of programs, even though the computers of that time were 20-40 times slower than the ones we use today.

But at that time, the three functional programmers were beginning to use graphical workstations instead of simple text terminals. They were unhappy about the fact that they did not have a way to write programs with graphical user interfaces in their functional language.

The two younger of the three functional programmers decided to start working on a solution to this problem. The older of the three was a bit skeptical and said that it would probably not be possible to obtain a solution that was efficient enough to write ``real'' programs with.

The two younger implemented an interface that allowed LML programs to talk to the X Windows system. They also designed an abstraction to be used as the basic building block when constructing graphical user interfaces. This abstraction was later named the Fudget.

The first X Windows interface was implemented as a separate program that the LML program could talk to via ordinary text I/O. The oldest programmer later integrated the interface with the run-time system of the LML compiler, making the interface much more efficient.

Approximately one year later, the two younger functional programmers felt they had a reasonably efficient system and a fairly nice abstraction. They wrote a paper about it and it was accepted at a functional programming conference [CH93b]. One of the younger functional programmers wrote some more about it and turned it into a licentiate thesis [CH93a].

The work continued. A number of improvements to make it easer to write programs were made, and the library was converted into Haskell. Improvements to the layout system allowed layout and plumbing to be specified separately. A lot of distracting extra function arguments could be removed after a parameter passing mechanism with default values was introduced. The resulting version of the Fudget library was presented at the Spring School on Advanced Functional Programming in Båstad in 1995 [HC95].

I Introduction

1 Programming by combination

This thesis is, to a large extent, oriented around programming by combination. By this, we mean the important programming method where you make programs by combining subprograms. The inner details of the subprograms can then be abstracted from, which makes it possible for the human brain to create and understand very complex programs. This methodology has, of course, been practised for many decades in various programming languages. However, it is a method that sometimes is forgotten, and often only used in parts of a program; for example, when doing tasks related to the operating system.

For programming by combination to be pervasive, it is important not only that we have access to a good library of subprograms, but the programming activity must also deal with forming new subprograms suitable for combination. Otherwise, the variety of programs we can write becomes limited because they get too complex. Therefore, programming by combination is also about forming new levels of subprograms.

One important aspect of programming is, of course, which programming language one uses. Different programming languages vary strongly in the support they give us when we want to program by combination. This is especially true when it comes to forming new subprograms. The authors have found that programming languages which are based on the declarative style are suitable in this respect. Declarative programming languages allow us to write programs in a mathematical style. For example, consider the expression

f((a + b) / 2,(a + b) / 2)

In a declarative programming language, we might identify a subprogram which we can name average.

let average = (a + b) / 2 

in f(average,average)

It is important that the activity of forming subprograms should be as easy as possible for the programmer. If the programmer is required to write many more characters than are shown in the previous example, another programming method might become more attractive, namely programming by copy and paste. This will soon result in programs which are complex to understand and maintain, but unfortunately, it is a too widely practised method.

The previous example did not actually introduce a subprogram. It could simply be seen as declaring a local variable. However, in declarative programming languages, we can use the same style when we want to form subprograms. The expression

f(a,a+b) + f(a,a+c) + f(a,a+d)

uses a recurring calling pattern to the function f. This pattern is easily captured by a subprogram that we can call

f2

let f2(x) = f(a,a+x)

in f2(b) + f2(c) + f2(d)

Forming a corresponding subprogram in the popular programming language C, for example, would be more involved. We would first need to declare a new top-level function, then make sure that its name did not collide with some other top-level function in the same source file, and finally, the function would need an extra parameter for the variable a. All parameters would need some type declaration.

As a more advanced example of programming by combination in declarative style, we might consider parsing combinators [Bur75][Wad85] (from now on, we will often talk about combinators when we mean subprograms which are designed for versatile combination). A large number of text parsers can be formed by four combinators:

token(c), which accepts the character c.
p ||| q, which forms an alternative: it either accepts whatever the parser p accepts, or it accepts whatever the parser q accepts.
p >>> q, which forms a sequence: it first accepts whatever p accepts, and then accepts whatever q accepts when given the rest of the text.
epsilon, which parses the empty string.

From these combinators, a programmer might build more useful combinators. Here is a combinator which can be used for parsing things within parentheses:

withinParentheses(p) = token('(') >>> p >>> token(')')

Or we might declare the combinator many(p), which forms a parser which accepts whatever p accepts, zero or more times in a sequence (this is often written p*):

many(p) = (p >>> many(p)) ||| epsilon

Note that in most of these combinators, we have used the possibility to parameterise over subprograms, which is another important feature that declarative programming languages naturally support.

2 Combinator libraries replace tools

Why would we want to use parsing combinators when we could instead use a parser generator tool? A parser generator like Yacc [Joh75] comes with a special programming language suitable for the task of specifying parsers. Although this is a quite powerful tool, it comes with a price, in that we have to learn this new programming language. Other tools (for example for specifying graphical user interfaces), also come with their own, domain-specific programming languages. Although they are often superb in many cases, they all have in common that the programmer must learn a quite new syntax, and often, the possibilities for the programmer to form new abstractions are poor. In the case of Yacc, it is not possible to express the abstraction


    withinParentheses

, for example. It is also hard or impossible to share abstractions between the different tool languages and the programmer's general programming language, something which adds to the overall complexity of a software system.

To return to our example, parsing combinators allow us to smoothly integrate parsers in our software without any additional tools, languages or compilers. We only need a library for parsing combinators. More generally, combinator libraries can be seen as defining an embedded language inside our general programming language. This way, the number of concepts a programmer has to learn decreases drastically, since the general programming language's idioms apply directly.

However, it should be noted that combinator libraries often miss features that specialised tools have (like efficiency). It is a challenge for creators of combinator libraries to catch up with this.

3 Declarative programming and input/output

In later sections, we will describe how one can use combinators for programming input/output. But before that, we will discuss how output can be done in a declarative programming language. Output from a program can also be seen as an effect that the program has on the outside world. When combining effects, their order is often highly important (the reader might want to try different combinations of the effects ``Open door'', and ``Walk through door'', for example). This is an important aspect which we must have in mind when considering subprograms for defining effects.

There are two widely used styles for dealing with effects in declarative programming languages. We either allow all subprograms to directly have effects on the outer world, or we only allow subprograms to return values that represent effects.

Consider a subprogram in a programming language using direct effects. If the subprogram is a function that returns some value, it is often said that the function can have a side effect while computing its value. The order in which these side effects happen is made precise by defining a computation order for expressions. This is most easily done by saying that all arguments to subprograms should be computed left to right, and then the subprogram is called. Also, an expression which uses a local definition should compute the definition before the expression. Such programming languages are called strict.

Side effects can interact with the programmer's activity of forming new subprograms, or naming subexpressions. For example, it is no longer clear that we could write

let average = (a + b) / 2 

in f(average,average)

instead of

f((a + b) / 2,(a + b) / 2)

because a potential side effect of the subprogram a would be carried out once in the first case, but twice in the second.

Another problem with combinator programming in strict programming languages is that we must be much more careful when defining combinators in terms of themselves. If we use the definition

many(p) = (p >>> many(p)) ||| epsilon

for many, we end up in an infinite loop, if arguments are computed strictly.

It is a very desirable feature of a programming language that subprograms do not have side effects. This feature is used in the non-strict, purely functional programming languages that we will use in the rest of this thesis. The term ``purely functional'' means that it is guaranteed that a function always return the same value if its arguments have the same value, and that it does not have any side effect. More generally, if the same expression occurs in many places (as a above, for example), it is guaranteed that all those occurrences compute to the same value. It is only in a purely functional programming language that we can introduce the variable average in the previous example, regardless of what a and b are.

In purely functional languages, we use the second way of dealing with effects, where subprograms may return values that represent effects, instead of performing them directly. A representation of an effect can then be combined with other representations of effects, yielding a new representation of an effect. Finally, the effect that our whole program represents is carried out. This means that issues of effects and computations are separated. When defining and combining effects, we do not have to bother about which parts of our program should be computed, how many times they might be computed, and in which order.

Having combinators that return representations of effects opens up the possibility to manipulate these effects before they are carried out. This can be used to adapt the effects of existing combinators to new situations.

In what follows, we will often speak about combinators having various effects, or doing various kind of input/output. At times, it will be convenient to think that the combinators actually perform these effects directly, but it is important to remember that they only define a representation of an effect.

4 I/O in functional languages?

A program in a pure functional language is an expression that denotes the effect that the program should have on the outside world when the program is executed. The question we turn to now is: how are the basic effects specified and how are effects combined?

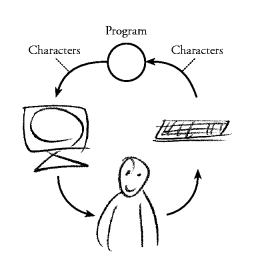
Suppose the outside world is a simple text terminal (see Figure 1). Then, the interesting effects are: outputting characters to the terminal screen, and inputting characters from the terminal keyboard. The behaviour of a program could be described by a sequence of the basic effects, so it is natural to use sequential compositions of effects to build programs with nontrivial behaviour. This is what is provided in the typical imperative languages.

Figure 1. A program and a user interacting via a text terminal.

As an example, consider a program that reads some numbers separated by white space, and outputs the sum of the numbers. In an imperative language, it would look something like this:

program = sumNumbers 0

sumNumbers acc =
  if end_of_input
  then putNumber acc
  else do n <- getNumber
          sumNumbers (acc+n)

getNumber = ...
putNumber = ...

We can identify the subprograms getNumber and


    putNumber

as reusable components. By taking a step back and reflecting on what a program is, we can perhaps find ways of composing programs other than the sequential composition of effects. Having more versatile ways of composing programs is likely to give us more opportunities to construct reusable subprograms.

We choose to view programs as defining stream processors, that is, a program describes some kind of process that consumes an input stream and produces an output stream. This view goes back to Landin [Lan65]. We use the symbol shown in Figure 2 to denote a stream processor.

Figure 2. A stream processor.

A stream processor can be seen as a function on streams. A program that interacts with a text terminal could be seen as a function from a stream of characters to a stream of characters. When the program is run, the function is applied to the stream of characters received from the keyboard and the resulting stream of characters is output to the screen.

In a lazy functional language, streams can be represented as ordinary lists. A program that interacts with a text terminal can thus be built using ordinary list functions. The typical lazy functional solution to the number-summing problem looks something like this:

program = show . sum . map read . words

The input stream is chopped into words, the words are converted to numbers, the numbers are summed and converted back into characters that can be output to the screen.

Let us compare this solution with the imperative one. In both solutions, subprograms for parsing and printing numbers are reusable. In the functional solution the number-summing function is reusable as well. And although we have used a standard function to sum a list of numbers, the above program can execute in constant space, since in a lazy language, computations are performed on demand. Likewise, input from the terminal is read on demand, allowing the computation of the sum to be interleaved with the reading and parsing of keyboard input. (If we tried to use the sum function in the imperative solution, we would first have to read all the numbers and store them in a list, and then call the sum function. The program would thus not run in constant space.)

In the functional solution, the program is no longer expressed as a composition of basic effects. Instead, we have built the program from a number of stream processors in a pipe line.

We have now seen two ways of describing stream processors:

the basic way of using sequential composition of I/O operations,
the more high-level way of using serial composition of stream processors.

5 What is a Fudget?

Previously, we looked at programs that communicate with a text terminal. We now refine the view of the outside world and consider graphical user interfaces (GUIs). In contrast to the typical text terminal program, which interacts with the user through a dialogue and thus is sequential in nature, programs with graphical user interfaces interact with the user by showing a window which can be seen as a control panel providing various control and indicator devices. The various devices exist in parallel in the window and their respective behaviours are mostly independent of other devices. This suggest that programs with graphical user interfaces should be built using some kind of parallel composition rather than sequential composition.

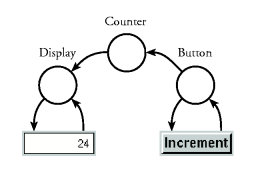
To illustrate what kind of program structure we are looking for, take a look at the counter example (pun intended). The user interface should contain two GUI elements: a button and a numeric display. Each time the button is pressed, the number in the display is incremented. We would like the program to contain one stream processor per GUI element, taken from a library (often called GUI toolkit or widget set), and an application-specific stream processor that counts the button presses and outputs numbers to the numeric display. The stream processors should be connected as in Figure 3.

Figure 3. The desired program structure of the counter example.

The key idea is that stream processors from the library handle the low-level details of the GUI elements, and the code that the application programmer writes, communicates with the GUI elements on a higher level of abstraction.

GUI elements can be seen as a particular kind of I/O device that a program can communicate with. The idea naturally extends to communication with other types of I/O devices, such as other computers on the Internet.

Our solution to building programs with this structure in a purely functional language, is based on a special kind of stream processor, the Fudget (see Figure 4. ``Fudget'' is an abbreviation of functional widget, where widget is an abbreviation of window gadget).

Figure 4. The Fudget.

A fudget has both low-level streams and high-level streams. The low-level streams are always connected to the I/O system, allowing the fudget to control a GUI element by receiving events and sending commands to the window system. The high-level streams can carry arbitrary (usually more abstract) values, and they connect the fudgets that make up a program in an application-specific way.

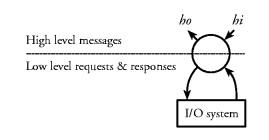
We will write the type of a fudget as

F hi ho

where hi and ho are the types of the messages in the high-level input and output streams, respectively.

The high-level streams between fudgets are connected by the programmer using combinators. Three basic ways to combine fudgets (and stream processors in general) are serial composition, parallel composition and loops, see Figure 5.

Figure 5. Serial composition, parallel composition, and loop.

The types of these combinators are: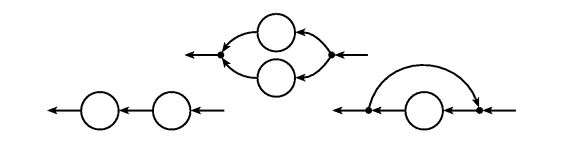

>==< :: F a b -> F c a -> F c b -- serial composition
>*< :: F a b -> F a b -> F a b -- parallel composition
loopF :: F a a -> F a a -- loop

These simple ideas allow programs with graphical user interfaces to be built in a hierarchical way using a declarative style. For example, the counter example can be expressed as

displayF >==< counterF >==< buttonF "Increment"

that is, a serial composition of three fudgets, where


    displayF

and buttonF handle the widgets that the user interacts with, and counterF just counts the button presses.

Serial composition is closely related to ordinary function composition. With this in mind, one can see that the program has much the same structure as the Landin stream I/O number-summing example shown in Chapter 4. Examples like this one will be explained further in Chapter 9.

6 Contributions of the thesis

The work presented in this thesis started with the desire to write programs with graphical user interfaces in a purely functional language. We also wanted to implement the GUI toolkit itself in the functional language. The questions we asked ourselves were:

Would the features of functional languages be appropriate for this task? Functional languages were known to be weak when it came to I/O. Implementations of GUI toolkits had traditionally been done in an object-oriented style. Lacking features such as subtypes, inheritance and parallelism, would a functional language still suffice?
Would implementations of functional languages be efficient enough to cope with the potentially large volume of I/O and high requirements on response times?

We believe that the thesis shows that the answer is yes to both of these questions.

The main result of the work behind this thesis is the Fudget library, which is an implementation of the ideas outlined in the previous section. Among other things, it provides

types and combinators for fudgets and stream processors,
a GUI toolkit, providing the usual widgets, and
support for network communication.

The Fudget library shows how a concurrent programming paradigm can be implemented and applied in a purely functional programming language.

We demonstrate the practical usefulness of the Fudget library by presenting a number of application programs, some of which are quite large. A number of programming styles and methods are presented which can be used when programming with Fudgets.

7 Road-map

Part II deals mainly with what a programmer can do with Fudgets. It begins with a brief introduction to Haskell (Chapter 8). The next chapter is a tutorial (Chapter 9), where a number of fudget programs are presented, ranging from the tiniest ``Hello world'' fudget to a simple calculator, and continues with an overview of the most important stuff that a programmer can use in the Fudget library. This includes an overview of some basic GUI building blocks (Chapter 10), how to specify layout (Chapter 11), a description of how to attach application-specific code to the Fudget library components (Chapter 12), how to combine fudgets (Chapter 13), and how to customise fudgets (Chapter 15).
Part III distills the fudget concept to get stream processors, which can be regarded as a simplification of fudgets, that do not necessarily need I/O. The last chapter in this part (Chapter 19) gives some programming examples using plain stream processors.
The reader interested in how the Fudget library works can continue with Part IV, which is devoted to the design and implementation. It also describes extensions and programming methods, as outlined further in its introduction. The last chapter (Chapter 31) describes how an existing functional GUI toolkit was implemented on top of Fudgets.
Part VI starts with a discussion of the efficiency of Fudget programs in Chapter 39, and suggests some possible program transformations for speed-up. In Chapter 40, we comment on the programming language Haskell itself, describe some problems, and discuss extensions. Chapter 41 discusses related work and presents a number of other functional GUI toolkits that have emerged. Chapter 42 contains a brief evaluation and conclusions. Some suggestions for future research, including a more formal study of stream processors, is given in Chapter 43.

II Programming with Fudgets

The fudget concept and the Fudget library was first conceived and designed as an aid in constructing graphical user interfaces in a lazy functional language. Although the Fudget library now supports other kinds of I/O, the main part of the library still relates to GUI programming.

In the Fudget library, each GUI element is represented as a fudget. The library provides fudgets for many common basic building blocks, like buttons, pop-up menus, text boxes, etc. The library also provides combinators that allow building blocks to be combined into complete user interfaces.

This section introduces the Fudget library by presenting a number of GUI programming examples. They illustrate the basic principles of how to create complete programs from GUI elements and application-specific code. After the examples follows an overview of the library. We show

some common GUI fudgets from the library,
how to specify the layout of GUIs,
different ways of writing abstract fudgets, and introduce stream processors,
combinators for building networks of fudgets, and
a scheme for parameter passing with default values.

8 A brief introduction to Haskell

The purely functional programming language that we will use in the rest of the thesis is Haskell [Pet97]. An introduction can be found at [HPF97], and there are also two reports that define the language and its standard libraries [PH97b][PH97a].

We believe that the program examples will be readable without detailed knowledge of Haskell--familiarity with some functional language is hopefully sufficient. However, some recurring patterns are perhaps worth explaining:

Haskell uses layout (indentation) rather than delimiting character to separate declarations, branches in case expressions, etc.
Anonymous functions are written using \ and ->: for example, \ x -> x is the identity function.
The operator . is function composition.
The operator $ is just function application, that is f $ x = f x. It is right associative and has low precedence, so it can be used to avoid nested parentheses. We often write expressions like
```
f $ g $ h $ \ x -> x + 1
```
instead of
```
f (g (h (\x -> x + 1)))
```
An ordinary alfanumeric identifier can be used as an infix operator by enclosing it in back quotes. We sometimes write, for example,
```
f x `ap` y
```
instead of
```
ap (f x) y
```
Infix operators are turned into functions that can be passed as arguments by enclosing parentheses. For example, (*) is equal to \x y -> x * y.
Operators can be partially applied using sections, again using parentheses. For example, (2/) is the function \x -> 2 / x, and (/2) is the function \x -> x / 2.
The Haskell syntax for tuples, lists and functions is chosen so that a type and the values of the type look similar. For example, the type of the tuple (3,False,"fudget") is (Int,Bool,String), the type of the list [1,2,3] is [Int] and the type of the function \ x -> x is a -> a.
In type expressions, names starting with lower case letters are type variables and names starting with upper case letters are type constructors.
We often use the Haskell standard type Either for disjoint unions, defined as
```
data Either a b = Left a | Right b
```
and the type Maybe for optional values, defined as
```
data Maybe a = Nothing | Just a
```
The result of a Haskell program is the value bound to the identifier main. This value should be a representation of the effect (as discussed in Chapter 3) the execution of the program should have on the outside world. A program can be as simple as
```
main = print "Hello, world!"
```

A unique feature of Haskell is the type class system [WB89], which is a systematic treatment of overloading. A type class declaration introduces a number of functions that will be overloaded. An instance declaration gives definition of the overloaded functions for a particular type. For example, a standard type class in Haskell is the class for types that support equality:

class Eq a where
   (==) :: a -> a -> Bool

To allows boolean values to be tested for equality with the

==

operator, an instance declaration like the following can be used:

instance Eq Bool where
  True   == True   = True
  False  == False  = True
  _      == _      = False

For some standard type classes, instance declarations can be generated automatically by adding a deriving clause to the type definition:

data Bool = False | True deriving Eq

When an overloaded function is used in a new function definition, the overloading may be inherited by the new function. For example, consider the function elem that checks if a value occurs in a list, defined as

x `elem` [] = False
x `elem` (y:ys) = x==y || x `elem` ys

The type of elem is written

elem :: Eq a => a -> [a] -> Bool

where the part Eq a => is called a context. It means that the type variable a is restricted to range over types that are instance of the Eq class.

In Haskell 1.3, the class system was generalised to allow classes of type constructors [Jon93] instead of just classes of base types. Type variables were extended to range over type constructors. This means a that type scheme like a Int is allowed. The type variable a can be instantiated to, for example, Maybe and the list type constructor, giving the types Maybe Int and [Int], respectively.

The well known function map,

map :: (a->b) -> [a] -> [b]

which is defined for lists in many functional languages, can now be generalised by introducing the class Functor,

class Functor f where
   map :: (a->b) -> f a -> f b

Instances for the lists and the Maybe type can be defined as

instance Functor [] where
   map f []      = []
   map f (x:xs)  = f x : map f xs

instance Functor Maybe where
   map f Nothing   = Nothing
   map f (Just x)  = Just (f x)

However, the introduction of constructor classes was motivated by the change to monadic I/O (see Section 41.1.3) and a convenient syntax for monadic programming. The class Monad is defined as

class Monad m where
  return  :: a -> m a
  (>>=)   :: m a -> (a -> m b) -> m b

and the special do syntax for monadic expressions,

do x₁ <- m₁
   x₂ <- m₂
   ...
   m_n

is defined to mean the same as

m₁ >>= (\ x₁ ->
m₂ >>= (\ x₂ ->
...
m_n))

9 Your first 8 Fudget programs

In the following, we present 8 simple GUI programming examples. For each example, we show a window snapshot, the program text and explain the major points of the example. To keep the size of the presentation reasonable, many unimportant details are deliberately left unexplained. The reader is referred to the Fudget Library Reference Manual [CH97] for full information. In addition, the WWW version of this thesis contains hyper links into the Reference Manual for many combinators and types. The WWW version is located at

http://www.cs.chalmers.se/~hallgren/Thesis/

The window snapshots were made on a Unix workstation running the X Windows system and a window manager providing Windows-95-like window frames.

For practical details, such as where to get the Fudget library, which platforms are supported, and how to compile programs, see Appendix A.

9.1 "Hello, world!"

We begin with a simple program that only displays a message in a window. This example illustrates what the main program should look like, as well as some other practical details. As the window dump shows, the window manager adds a title bar to the message.

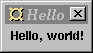Here is the source code:

import Fudgets

main = fudlogue (shellF "Hello" (labelF "Hello, world!"))

Note:

To use the Fudget library, the module Fudgets should be imported.
A fudget program consists of a number of fudgets combined in a hierarchical structure that makes up one main fudget. The function fudlogue,
```
fudlogue :: F a b -> IO ()
```
connects the main fudget to Haskell's I/O system, thus starting a dialogue between them. It sets up the communication with the window system, gathers commands sent from all fudgets in the program and sends them to the window system, and distributes events coming from the window system to the appropriate fudgets.
A fudget program with a graphical user interface needs one or more shell windows (top-level windows). These can be created with the function shellF,
```
shellF :: String -> F a b -> F a b
```
which given a window title and a fudget, creates a shell window containing the graphical user interface defined by the argument fudget. The fudgets for GUI elements, like labelF, can not be used directly on the top level in a program, but must appear inside a shell window.
In this simple program, the contents of the shell window are merely a simple string label, that is created with the function labelF,
```
labelF :: (Graphic a) => a -> F b c
```
The argument is the label to be displayed. The label can be a value of any type that is an instance of the Graphic class. The Fudget library provides instances for many predefined types, including strings. The Graphic class is discussed in Section 27.1.
Both the input and output types of labelF are type variables that do not occur anywhere else. This indicates that none of the high-level streams are used by labelF.
labelF has only one parameter: the label to be displayed. Most GUI fudgets come in two versions: a standard version, like labelF, and a customisable version, for example labelF', which allows you to change parameters like fonts and colors, for which the standard version provides default values. See Chapter 15 for more details.
The size and placement of the GUI elements need not be specified. The fudget system automatically picks a suitable size for the label and the size of the shell is adapted to that.

Useful programs of course contain more than one GUI element. The next example will contain two GUI elements!

9.2 The factorial function

This program illustrates how data is communicated between different parts of a Fudget program. It illustrates a simple way to combine application-specific code (in this case the factorial function) with GUI elements from the Fudget library.

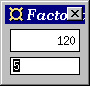The program shows a numeric entry field at the bottom and a number display at the top. Whenever the user enters a number in the entry field and presses the Return key, the factorial of that number is computed and displayed in the number display.

Here is the source code:

import Fudgets

main = fudlogue (shellF "Factorial" facF)

facF = intDispF >==< mapF fac >==< intInputF

fac 0 = 1
fac n = n * fac (n-1)

Note:

The program facF is structured as a serial composition of three parts, using the operator >==<. Notice that, as with ordinary function composition, data flows from right to left. The parts are:
- the numeric entry field intInputF,
- mapF fac, an abstract fudget (a fudget without a corresponding GUI element) that applies fac, the factorial function, to integers received from the entry field, and
- the number display intDispF, which displays the computed factorials.
We have used fudlogue and shellF on the top level as in the previous examples (Section 9.1).

The types of the new library components used in this example are:

>==< :: F a b -> F c a -> F c b
intInputF :: F Int Int
mapF :: (a -> b) -> F a b
intDispF :: F Int a

Although this program does something useful (at least compared to the two previous examples), it could be made more user friendly, e.g., by adding some explanatory text to the user interface. The next example shows how to do this.

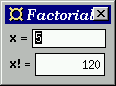9.3 The factorial function, with improved layout

This program shows how to use layout combinators to improve the visual appearance of a Fudget program.

We have made the factorial function example from Section 9.2 more self documenting by adding labels to the entry field and the output display. We have also changed the order of the two parts: the entry field is now above the display.

Here is the source code:

import Fudgets

main = fudlogue (shellF "Factorial" facF)

facF = placerF (revP verticalP) (
        ("x! =" `labLeftOfF` intDispF) >==<
        mapF fac >==<
        ("x =" `labLeftOfF` intInputF))

fac 0 = 1
fac n = n * fac (n-1)

Note:

We have used the function labLeftOfF to put labels to the left of the entry field and the display. (In Haskell, back quotes can be used to turn any function into an infix operator, as we have done with labLeftOfF here).
The function placerF can be applied to a composition of fudgets to specify the relative placement of the parts. (The layout system automatically picks some placement if layout is left unspecified.) The first argument to placerF is a placer, in our case revP verticalP, where verticalP causes the parts to be stacked vertically, with the leftmost fudget in the composition at the top, and revP reverses the order of the parts.
Everything else is as in the previous examples.

The types of the new library components used in this example are:

labLeftOfF :: (Graphic a) => a -> F b c -> F b c
placerF :: Placer -> F a b -> F a b
revP :: Placer -> Placer
verticalP :: Placer

9.4 An up counter

This program illustrates a more general way to combine application-specific code with GUI elements from the Fudget library. It illustrates that state information can be encapsulated. State information is often considered as difficult to handle in pure functional languages; hopefully, this counter example shows how easy it is!

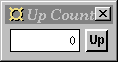This program has a button and a numeric display. Pressing the button increments the number in the display.

The application-specific code in this example sits between the button and the display. It maintains an internal counter which is incremented and output to the display whenever a click is received from the button.

Here is the source code:

import Fudgets

main = fudlogue (shellF "Up Counter" counterF)

counterF = intDispF >==< mapstateF count 0 >==< buttonF "Up"

count n Click = (n+1,[n+1])

Note:

As with the factorial example (Section 9.2), the central part of the program (counterF) is a serial composition of three parts. At the output end we see the familiar intDispF. At the input end of the pipe line is a button created with buttonF. It outputs a Click when pressed. The middle component maintains an internal counter. The counter is incremented and output to the display when a Click is received from the button.
mapstateF, like mapF, allows messages sent between fudgets to be processed in an application-specific way. With mapstateF, an arbitrary number of messages can be output as response to an input message. In addition, the output can depend not only on the current input, but also on an internal state. mapstateF has two arguments: a state transition function and an initial state. When applied to the current state and an input message, the state transition function should produce a new internal state and a list of output messages.
The function count is the state transition function in this program.
There is a small pitfall in this program: intDispF automatically displays 0 when the program starts. The initial value of the counter happens to be 0 as well. If the 0 is changed in the definition of counterF, the display will still show 0 when the program starts. One way to fix this is to use the customisable version of intDispF to specify the initial value to display.

The types of the new library components used in this example are:

buttonF :: (Graphic a) => a -> F Click Click
data Click = Click
mapstateF :: (a -> b -> (a, [c])) -> a -> F b c

This and the previous examples show how serial composition creates a communication channel from one fudget to another. But what if a fudget needs input from more than one source? The next example shows one possible solution.

9.5 An up/down counter

This example illustrates how to handle input from more than one source (Figure 6).

Figure 6. The up/down counter.

The two buttons affect the same counter.

Here is the source code:

import Fudgets

main = fudlogue (shellF "Up/Down Counter" counterF)

counterF = intDispF >==< mapstateF count 0 >==<
           (buttonF filledTriangleUp >+< 
            buttonF filledTriangleDown)

count n (Left Click)   = (n+1,[n+1])
count n (Right Click)  = (n-1,[n-1])

Note:

The up/down counter is a small extension of the Up Counter (Section 9.4). We have added a button by replacing
```
buttonF ...
```
with
```
(buttonF ... >+< buttonF ...)
```
using the operator >+< for parallel composition.
The output from a parallel composition is the merged output from the two components. Output from the left component is tagged Left and output from the right component is tagged Right. The constructors Left and Right are constructors in the datatype Either.
The count function will now receive Left Click or Right Click, depending on which button was pressed. It has been adjusted accordingly. (Note that Left Click and Right Click have nothing to do with the left and right mouse buttons!)
Just to illustrate that buttons can display arbitrary graphics and not just text, we have used two suitable shapes that happen to be provided by the library.
Everything else is as in the previous example (Section 9.4).

The types of the new library components used in this example are:

>+< :: F a b -> F c d -> F (Either a c) (Either b d)
filledTriangleUp :: FlexibleDrawing
filledTriangleDown :: FlexibleDrawing

9.6 An up/down/reset counter

This example shows how to create parallel compositions of many fudgets of the same type.

This program extends the counter example with yet another button. The counter can now be incremented, decremented and reset.

Here is the source code:

import Fudgets

main = fudlogue (shellF "Up/Down/Reset Counter" counterF)

counterF = intDispF >==< mapstateF count 0 >==< buttonsF

data Buttons = Up | Down | Reset deriving Eq

buttonsF = listF [(Up,     buttonF "Up"     ),
                  (Down,   buttonF "Down"   ),
                  (Reset,  buttonF "Reset"  )]

count n (Up,     Click) = (n+1,  [n+1])
count n (Down,   Click) = (n-1,  [n-1])
count n (Reset,  Click) = (0,    [0])

Note:

When putting more than two fudgets of the same type in parallel, it is more convenient to use listF than >+<. The argument to listF is a list of pairs of addresses and fudgets. The addresses are used when messages are sent and received from the components in the composition.
In this program there is a user defined enumeration type Buttons, the elements of which are used as the addresses of the buttons. The messages received by the count function are pairs of Buttons values and Clicks.
Everything else is as in the previous example (Section 9.5).

The type of the new library component used in this example is:

listF :: (Eq a) => [(a, F b c)] -> F (a, b) (a, c)

9.7 A loadable up/down counter

This example illustrates the use of loops to handle user-interface elements that are used for both input and output (Figure 7).

Figure 7. The loadable up/down counter.

The program extends the up/down counter in Section 9.5 by allowing the user to set the counter to any value by entering it in the display field.

Here is the source code:

import Fudgets

main = fudlogue (shellF "Loadable Up/Down Counter" counterF)

counterF = loopThroughRightF (mapstateF count 0) intInputF >==<
           (buttonF filledTriangleUp >+< buttonF filledTriangleDown)

count n (Left n')              = (n',   [])
count n (Right (Left Click))   = (n+1,  [Left (n+1)])
count n (Right (Right Click))  = (n-1,  [Left (n-1)])

Note:

Instead of intDispF we have used intInputF, which not only displays numbers, but also allows the user to enter numbers.
We have used the combinator loopThroughRightF to allow the count function to both receive input from and send output to intDispF. In the composition loopThroughRightF fud₁ fud₂, fud₁ handles the communication with the outside world (the buttons in this example), while fud₂ can communicate only with fud₁, and is in this sense encapsulated by fud₁. In fud₁, messages to/from fud₂ are tagged Left and messages to/from the outside world are tagged Right.

The type of the new library component used in this example is:

loopThroughRightF :: F (Either a b) (Either c d) -> F c a -> F b d

9.8 A simple calculator

As a final example, we show how a slightly larger program, a simple calculcator, can be built using the ideas illustrated by the previous examples (Figure 8).

Figure 8. The calculator.

For simplicity, postfix notation is used, i.e., to compute 3+4 you enter 3 Ent 4 +. The source code can be found in Figure 9.

import Fudgets

main = fudlogue (shellF "Calculator" calcF)

calcF = intDispF >==< mapstateF calc [0] >==< buttonsF

data Buttons = Plus | Minus | Times | Div | Enter | Digit Int deriving Eq

buttonsF = placerF (matrixP 4) (
              listF [d 7,   d 8,  d 9,  op Div,
                     d 4,   d 5,  d 6,  op Times,
                     d 1,   d 2,  d 3,  op Minus,
                     hole,  d 0,  ent,  op Plus])
  where
    d n = (Digit n,buttonF (show n))
    ent = op Enter
    hole = (Enter,holeF)
    op o = (o,buttonF (opLabel o))
      where  opLabel Plus   = "+"
             opLabel Minus  = "-"
             opLabel Times  = "*"
             opLabel Div    = "/"
             opLabel Enter  = "Ent"

calc (n:s)    (Digit d,_)  = new (n*10+d) s
calc s        (Enter,_)    = (0:s,[])
calc (y:x:s)  (Plus,_)     = new (x+y) s
calc (y:x:s)  (Minus,_)    = new (x-y) s
calc (y:x:s)  (Times,_)    = new (x*y) s
calc (y:x:s)  (Div,_)      = new (x `div` y) s
calc s        _            = (s,[])

new n s = (n:s,[n])

Figure 9. Source code for the calculator.

Note:

The program structure is much the same as in the up/down/reset counter (Section 9.6).
To specify the placement of the buttons we have used placerF (as in Section 9.3) and the placer matrixP which has the number of columns as an argument.
The state maintained by the application-specific code (the function calc) is a stack (represented as a list) of numbers. The function calc pushes and pops numbers from the stacks as appropriate. The last clause in the definition means that nothing happens if there are too few values on the stack for an operation.
As it stands, the calculator can be controlled with the mouse only. The customisable version of buttonF allows you to specify a keyboard shortcut for the button. It would thus be relatively easy to make the calculator controllable from the keyboard.

The type of the new library component used in this example is:

matrixP :: Int -> Placer

10 Fudget library GUI elements

In this chapter, we present some common GUI elements provided by the Fudget library. For more information, consult the reference manual, which is available via WWW [HC97].

Before we introduce the GUI elements, we discuss briefly how fudget programs are formed using the function fudlogue.

10.1 Functions used on the top level of programs

As we have seen in the examples in Chapter 9, a fudget program consists of a number of fudgets, combined in a hierarchical structure that makes up one main fudget of type


    F a b

, for some types a and b. The main program in Haskell should have type IO (), so we need a glue function to be able to plug in the main fudget. The function fudlogue is provided for this purpose:

fudlogue :: F a b -> IO ()

The main program of a fudget program usually consists just of a call to fudlogue with an argument fudget. like

main :: IO ()
main = fudlogue the_main_fudget

However, it is possible to combine fudlogue with other monadic I/O operations. For example, to create a program that starts by reading some configuration file, you could write

main = do config <- readFile config_filename
          fudlogue (main_fudget config)

Programs with graphical user interfaces need at least one shell (top-level) window. These are created with the function shellF:

shellF :: String -> F a b -> F a b

The typical GUI program has only one shell window, and the main program thus looks something like

main = fudlogue (shellF window_title main_gui_fudget)

A program with more than one shell window could for example look something like

main = fudlogue (shellF title₁ fud₁ >==< shellF title₂ fud₂)

The fudget shellF is not restricted to the top level. You could write the above example as

main = fudlogue (shellF title₁ (fud₁ >==< shellF title₂ fud₂))

and achieve the same result.

10.2 Displaying values

We have already seen labelF, which displays static labels, and intDispF, which displays numbers that can change dynamically. There is also displayF,

displayF :: (Graphic a) => F a b

a more general display for dynamically changing values. It can display values of any type in the Graphic class. It could in fact also display numbers, but intDispF has the advantage that the numbers are displayed right adjusted.

10.3 Buttons

We have already seen buttonF,

buttonF :: (Graphic a) => a -> F Click Click

in the examples above. It provides command buttons, i.e., buttons trigger some action when pressed. The Fudget library also provides toggle buttons and radio groups (Figure 10). Pressing these buttons causes a change that has a lasting visual effect (and probably also some other lasting effect). A toggle button changes between two states (on and off) each time you press it. A radio group allows you to activate one of several mutually exclusive alternatives. The types of these fudgets are

toggleButtonF :: (Graphic a) => a -> F Bool Bool
radioGroupF :: (Graphic b, Eq a) => [(a, b)] -> a -> F a a

The input messages can be used to change the setting under program control.

toggleButtonF "Run"

radioGroupF [(1,"P1"),(2,"P2"),(3,"P3"),(0,"Off")] 0
Figure 10. Toggle buttons and radio groups.

10.4 Menus and scrollable lists

Menus serve much the same purpose as buttons, but they save screen space by appearing only when activated. The fudget


      menuF name alts

, where

menuF :: (Graphic a, Graphic c) => a -> [(b, c)] -> F b b

provides pull-down menus. name is the constantly visible name you press to activate the menu and alts is the list of menu alternatives.

The fudget

popupMenuF :: (Graphic b, Eq b) => 
       [(a, b)] -> (F c d) -> F (Either [(a, b)] c) (Either a d)

provides pop-up menus, i.e., menus that are activated when a certain mouse button (the third by default) is pressed over some screen area. The fudget

popupMenuF 
      initial_menu fud

creates a fudget which behaves like the fudget fud with the addition that the menu initial_menu pops up when the user presses the third menu button. You communicate with the fudget as with a tagged parallel composition of the menu and the fudget fud. Messages to/from the menu are tagged Left and messages to/from fud are tagged Right. You can replace the initial_menu by sending Left new_menu to the fudget.

As an example, suppose we wanted a compact version of the counter in Section 9.6. We could then replace the three buttons with a pop-up menu attached to the display. The source code for this and the resulting user interface is shown Figure 11. We have used the combinator serCompLeftToRightF, which turns a parallel composition into a serial composition (see Section 13.1).

import Fudgets

main = fudlogue (shellF "Compact Up/Down/Reset Counter" counterF)

counterF =
  serCompLeftToRightF
    (popupMenuF menu (intDispF >==< mapstateF count 0))

data Buttons = Up | Down | Reset deriving Eq

menu = [(Up, "Up"), (Down, "Down"), (Reset, "Reset")]

count n Up     = (n+1,  [n+1])
count n Down   = (n-1,  [n-1])
count n Reset  = (0,    [0])

Figure 11. A compact version of the up/down/reset counter presented in Section 9.6.

Figure 12. pickListF

Figure 13. stringInputF

When the number of alternatives is large, or when they change dynamically, you can use a scrollable list instead of a menu. The function

pickListF :: (a -> String) -> F (PickListRequest a) 
                                (InputMsg (Int, a))

(shown in Figure 12) takes a show function and returns a fudget that displays lists of alternatives received on the high-level input. When an alternative is selected, by clicking on it, it will appear in the output stream. Actually, the output from pickListF is of type InputMsg, which is explained in Section 10.5.1 below.

The values in the input stream are of type PickListRequest to allow the list of alternatives to be modified in various ways. To replace the entire list, you can use

replaceAll :: [a] -> PickListRequest a

but there are other functions that let you insert new alternatives at some position in the list,

insertText :: Int -> [a] -> PickListRequest a

or, more generally, replace part of the list with new alternatives,

replaceText :: Int -> Int -> [a] -> PickListRequest a

and so on. The screen will be updated in an efficient way when you do modifications of this kind.

10.5 Entering values

Choosing an alternative from a list is usually easier than typing something, e.g., the name of a colour, on the keyboard. But when there is no predefined set of alternatives, you can use fudgets that allow the user to enter values from the keyboard. The library provides

stringInputF :: F String String
intInputF :: F Int Int

for entering strings and integers (see Figure 13). For entering other types of values, you can use stringInputF and attach the appropriate printer and parser functions.

10.5.1 More detailed information on user input

The fudgets stringInputF and intInputF do not produce any output until the user presses the Enter (or Return) key to indicate that the input is complete. This is often a reasonable behaviour, but there are versions of these fudgets that provide more detailed information:

stringF :: F String (InputMsg String)
intF :: F Int (InputMsg Int)

These fudgets output messages of type InputMsg, which contain the current contents of the entry field and an indication of whether the value is intermediate or complete.

There are some stream processors that are useful when post processing messages from entry fields:

stripInputSP :: SP (InputMsg a) a
inputLeaveDoneSP :: SP (InputMsg a) a
inputDoneSP :: SP (InputMsg a) a

The first one passes through all messages, so that you will know about all changes to the contents of the entry field. The second one outputs a message when the user indicates that the input is complete and when the input focus leaves the entry field. The last one outputs a message only when the input is indicated as complete.

The fudget stringInputF is defined as

stringInputF = absF inputDoneSP >==< stringF

As we saw above, the fudget pickListF also produces output of type InputMsg. In this case, input is considered to be complete when the user double clicks on an alternative. Hence you use stripInputSP if a single click should be enough to make a choice, and inputDoneSP if a double click should be required.

10.6 Displaying and editing text

The library provides the fudgets

moreF :: F [String] (InputMsg (Int, String))
moreFileF :: F String (InputMsg (Int, String))
moreFileShellF :: F String (InputMsg (Int, String))

which can display longer text.(Footnote: The names come from the fact that they serve the same purpose as the UNIX program


      more

.) The input to moreF is a list of lines of text to be displayed. The other two fudgets display the contents of file names received on the input. In addition, moreFileShellF appears in its own shell window with a title reflecting the name of the file being displayed.

There also is a text editor fudget (Figure 14),

Figure 14. The text editor fudget editorF.

which supports cut/paste editing with the mouse, as well as a small subset of the keystrokes used in GNU emacs. It also has an undo/redo mechanism.

10.7 Scroll bars

GUI elements that can potentially become very large, like


      pickListF

, moreF and editorF, have scroll bars attached by default. There are also combinators to explicitly add scroll bars:

scrollF, vScrollF, hScrollF :: F a b -> F a b

The v and h versions give only vertical and horizontal scroll bars, respectively. The argument fudget can be any combination of GUI elements.

11 Specifying layout

When combining fudgets for GUI elements, there are two considerations:

The data flow aspect: how should they communicate, i.e., should one use a serial, parallel, or some other combinator?
The visual aspect: how should the GUI elements be placed on the screen?

When developing fudget programs, it is not necessary to be concerned with the actual layout of the GUI fudgets. For example, the fudget

shellF "Buttons"
  (buttonF "A Button" >+< buttonF "Another Button")

will get some default layout which might look like Figure 15.

Figure 15. When no layout is specified in the program, the automatic layout system chooses one.

But sooner or later, we will want to have control over the layout. The GUI library lets us do this two different ways:

Combinator-based layout. This method is based on the combinator placerF that has appeared in some of the previous examples. It allows you to attach layout information to an arbitrary fudget. Usually, you first combine some fudgets using combinators like >+<, >==<, and listF, and then apply placerF to the combination to specify a layout. This is a fairly easy method for adding layout information to a program. However, the layout possibilities are somewhat limited by the structure of the program.
Name layout. Here, the layout is specified separately from the fudget structure. GUI fudgets are assigned names, which are later referred to in layout specifications placed inside each shellF.

Before describing these, we will present the layout combinators that both of them use.

11.1 Boxes, placers and spacers

Layout is done hierarchically. Each GUI fudget will reside in a box, which will have a certain size and position when the layout is complete. A list of boxes can be put inside a single box by a placer. A placer defines how the boxes should be placed in relation to each other inside the larger box. This enclosing box can be subject to further placement, but the enclosed boxes are hidden by the placer in the sense that they cannot be manipulated individually any more. The effects of some placers are illustrated in Figure 16.

Figure 16. Different placers.

The parameter to matrixP specifies the number of columns the matrix should have. The types of the placers are

horizontalP :: Placer
verticalP :: Placer
matrixP :: Int -> Placer
revP :: Placer -> Placer

The placer revP reverses the list of boxes it is applied to. Another higher order placer is flipP, which transforms a placer into a mirror symmetric placer, with respect to the line x = y (that is, it flips the x and y coordinates):

flipP :: Placer -> Placer

Hence, we can define verticalP as

verticalP = flipP horizontalP

Placers can be applied to fudgets by means of placerF:

placerF :: Placer -> F a b -> F a b

It applies the placer to all boxes in the argument fudget. The order of the boxes is left to right, with respect to the combinators listF, >==< and >+<, etc.

As an example, suppose we want to specify that the two buttons in Figure 15 should have vertical layout. We could then write

shellF "Buttons" (placerF verticalP (buttonF "A Button" >+<
                                     buttonF "Another Button"))

The result can be seen in Figure 17. In a similar way, the first button could be placed below, to the right of, or to the left of the second button, by using the placers

revP
      verticalP

, horizontalP or revP horizontalP, respectively.

Figure 17. The same GUI elements as in Figure 15, but the program explicitly specifies vertical layout.

Abstract fudgets do not have a corresponding box in the layout. This means that the presence of mapstateF in the definition of counterF in Figure 18, does not leave a hole in the layout of verticalCounterF.

verticalCounterF = placerF verticalP counterF

counterF = intDispF >==< mapstateF count 0 >==<
           (buttonF "Up" >+< buttonF "Down")
Figure 18. An up/down counter with vertical layout. Abstract fudgets do not have a corresponding box in the layout.

What if we want the display to appear between the two buttons? With the placers we have seen, the two buttons will appear together in the layout, since they appear together in the program structure. One solution is to use a placer operator that allows the order of the boxes to be permuted:

permuteP :: [Int] -> Placer -> Placer

We can then replace verticalP with

permuteP [2,1,3] verticalP

to get the display in the middle. This kind of solution works, but it will soon become quite complicated to write and understand. A more general solution is to use name layout (Section 11.2).

Placers are used to specify the layout of a group of boxes. In contrast, spacers are used to wrap a box around a single box. Spacers can be used to determine how a box should be aligned if it is given too much space, or to add extra space around a box. Examples of spacers that deal with alignment can be seen in Figure 19.

Figure 19. Spacers for alignment.

The topmost box (placed with 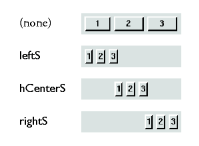horizontalP) must fill up all the available space. The lower three boxes have been placed inside a box which consumes the extra space. The spacers used are derived from the spacer hAlignS, whose argument states the ratio between the space to the left of the box and the total available extra space:

hAlignS :: Alignment -> Spacer
leftS = hAlignS 0
hCenterS = hAlignS 0.5
rightS = hAlignS 1

There is a corresponding spacer to flipP, namely


      flipS

. It too flips the x and y coordinates, and lets us define some useful vertical spacers:

flipS :: Spacer -> Spacer
vAlignS a = flipS (hAlignS a)
topS = flipS leftS
vCenterS = flipS hCenterS
bottomS = flipS rightS

With compS, we can compose spacers, and define a spacer that centers both horizontally and vertically:

compS :: Spacer -> Spacer -> Spacer
centerS = vCenterS `compS` hCenterS

To add extra space to the left and right of a box, we use


      hMarginS left right

, where

hMarginS :: Distance -> Distance -> Spacer
type Distance = Int

Distances are given in number of pixels.(Footnote: This is easy to implement, but makes programs somewhat device dependent.) From hMarginS, we can derive marginS, which adds an equal amount of space on all sides of a box:

vMarginS above below = flipS (hMarginS above below)
marginS s = vMarginS s s `compS` hMarginS s s

Spacers can be applied to fudgets by means of spacerF:

spacerF :: Spacer -> F a b -> F a b

The fudget spacerF s f will apply the spacer s to all boxes in f which are not enclosed in other boxes. We can also modify a placer by wrapping a spacer around the box that the placer assembles:

spacerP :: Spacer -> Placer -> Placer

For example, spacerP leftS horizontalP gives a horizontal placer which will left adjust its boxes.

11.2 Name layout

To separate layout from fudget structure, we put unique names on each box (usually corresponding to a simple GUI fudget) whose layout we want to control, by using nameF:

type LName = String
nameF :: LName -> F a b -> F a b

The layout of the boxes that have been named in this way, is specified using the type NameLayout. Here are the basic functions for constructing NameLayout values:

leafNL :: LName -> NameLayout
placeNL :: Placer -> [NameLayout] -> NameLayout
spaceNL :: Spacer -> NameLayout -> NameLayout

To apply the layout to named boxes, we use nameLayoutF:

nameLayoutF :: NameLayout -> F a b -> F a b

As an application of name layout, we show how the vertical counter in Figure 18 can be changed, so that the display appears between the up and down buttons (Figure 20):

nlCounterF = nameLayoutF layout counterF

counterF = nameF dispN intDispF
           >==< mapstateF count 0
           >==< (nameF upN    (buttonF filledTriangleUp) >+<
                 nameF downN  (buttonF filledTriangleDown))

-- only layout below
layout = placeNL verticalP (map leafNL [upN, dispN, downN])
upN = "up"
downN = "down"
dispN = "disp"

Figure 20. With name layout, the order of the GUI elements in the window does not have to correspond to their order in the program text.

Now, we can control the layout of the two buttons and the display, without changing the rest of the program.

The actual strings used for names are unimportant, as long as they are unique within the part of the fudget structure where they are in scope. So instead we can write

(upN:downN:dispN:_) = map show [1..]

11.3 Pros and cons of the different layout methods.

When it comes to specifying the layout of user interfaces, the Fudget library provides at least three solutions that differ in expressiveness and safety:

The don't care solution: ignore the problem. The programmer can compose a number of GUI fudgets using plumbing combinators, without specifying the layout. The system will automatically pick some layout. This is perfectly safe, but it obviously does not give the programmer any control over layout.
The combinator-based approach: the programmer inserts placerF applied to some placer at some selected points in the fudget hierarchy. This gives the programmer more control over layout and is still perfectly safe, but there is a coupling between how the fudgets have been composed and how they appear on the screen. This is not necessarily bad, but it limits the freedom in the choice of layout.
Name layout: the boxes of the GUI elements are labelled with unique names. On the top level of the program, the programmer inserts nameF applied to a layout specification which, by referring to the names, can achieve a layout of the GUI elements completely unrelated to how they were composed.
In this solution it is possible to make mistakes, however. For the layout specification to work properly, the name of every named box should occur exactly once in the layout specification. If you forget to mention a box, or if you mention it twice, or if you name a box that does not exist, the layout will not work properly. These mistakes are not detected at compile time, but give rise run-time errors or a weird layout.

The Fudget library thus offers safe solutions with limited freedom, and unsafe solutions with full freedom. With respect to safety and expressiveness, the solutions used in some other functional GUI toolkits, for example Haggis [FP96] and Gadgets [Nob95], are equivalent to name layout.

The problem with the name layout solution is that it requires a certain consistency between two different parts of the program. Maintaining this consistency during program development is of course an extra burden on the programmer.

Can a type system be used to make name layout safe? It would perhaps be possible to include layout information in some form in the types of GUI fudgets and catch some mistakes with the ordinary Haskell type system. However, the requirement that each name occurs exactly once in the layout specification suggests that you would need a type system with linear types [Hol88] to catch all mistakes.

12 Abstract fudgets

When using the Fudget library in a program, fudgets from the library are usually combined with some application-specific code, that is typically attached to the program in serial compositions. In the examples, we have seen the use of mapF and mapstateF for this:

facF = intDispF >==< mapF fac >==< intInputF

counterF = intDispF >==< mapstateF count 0 >==< buttonF "Up"

The functions mapF and mapstateF create abstract fudgets, that is, fudgets that do not perform any I/O. They communicate only via their high-level streams.

A more general way to construct abstract fudgets is provided by the function absF,

absF :: SP a b -> F a b

where SP is the type constructor for plain stream processors. These have a single input stream and a single output stream. The function absF creates a fudget by connecting the streams of a stream processor to the high-level streams of the fudgets, while leaving the low-level streams disconnected, as shown in Figure 21.

Figure 21. Turning a stream processor into an abstract fudget.

The functions mapF and mapstateF are in fact defined in terms of absF:

mapF = absF mapSP
mapstateF = absF mapstateSP

where mapSP and mapstateSP,

mapSP :: (a -> b) -> SP a b
mapstateSP :: (a -> b -> (a, [c])) -> a -> SP b c

are discussed in Section 16.2 and Section 16.3, respectively.

Although high-level combinators like mapF and mapstateF are adequate for most fudget application programming, some programmers may prefer the flexibility of the more basic ways of creating stream processors. Two examples where abstract fudgets are defined in terms of absF can be found in Section 32.4. An extensive discussion of stream processors can be found in Part III.

13 Fudget plumbing

We have already seen examples of how to use the fudget plumbing combinators. There are three basic forms of compositions: serial composition, parallel composition and loops.

-- Serial composition:
>==< :: F b c -> F a b -> F a c

-- Parallel composition:
>+< :: F i1 o1 -> F i2 o2 -> F (Either i1 i2) (Either o1 o2)
>*< :: F i o -> F i o -> F i o
listF :: (Eq t) => [(t, F i o)] -> F (t, i) (t, o)

-- Loops:
loopF :: F a a -> F a a
loopLeftF :: F (Either loop input) (Either loop output) -> F input output
loopThroughRightF :: F (Either oldo newi) (Either oldi newo) -> 
                     F oldi oldo -> 
                     F newi newo

The different fudget combinators treat the high-level streams in different ways, while the low-level streams are treated in the same way in all combinators. Figure 22 illustrates serial and parallel composition of fudgets.

Figure 22. Serial and parallel composition of fudgets.

Apart from the plumbing combinators listed above, the Fudget library contains further combinators that capture common patterns. Some of these combinators are described in the following sections.

The fudget combinators have corresponding combinators for plain stream processors, which are discussed in more detail in Chapter 17. Their names are obtained by replacing the F suffix with an SP, or substituting -...- for >...< in the operators.

13.1 Serial compositions

Serial composition connects the output of one fudget to the input of another fudget. As with function composition, data flow from right to left, so that in the composition

fud₂ >==<
      fud₁

, the output of fud₁ is connected to the input of fud₂.

Many of the examples in Chapter 9 contain serial compositions of the form

mapF f >==< fud
fud >==< mapF f

The library provides the following combinators to capture these cases:

>=^< :: F a b -> (c -> a) -> F c b
fud >=^< f = fud >==< mapF f

>^=< :: (a -> b) -> F c a -> F c b
f >^=< fud = mapF f >==< fud

(The library versions of >^=< and >=^< have more involved definitions to be more efficient.)

Compositions of the form

absF sp >==< fud
fud >==< absF sp

are also common. The library provides two operators for these special cases:

>^^=< :: SP b c -> F a b -> F a c
sp >^^=< fud = absF sp >==< fud

>=^^< :: F b c -> SP a b -> F a c
fud >=^^< sp = fud >==< absF sp

Some combinators, like popupMenuF (see Section 10.4), create parallel compositions of fudgets, but sometimes a serial composition is instead required. This could be accomplished by using a loop and an abstract fudget to do the necessary routing, but the library contains two combinators that do this:

serCompLeftToRightF :: F (Either a b) (Either b c) -> F a c
serCompRightToLeftF :: F (Either a b) (Either c a) -> F b c

The following equations hold:

serCompRightToLeftF (l >+< r) = l >==< r

serCompLeftToRightF (l >+< r) = r >==< l

13.2 Parallel compositions

When combining more than two or three fudgets, the tagging obtained by using >+< can become a bit clumsy. It may then be more convenient to use listF,

listF :: (Eq a) => [(a, F b c)] -> F (a, b) (a, c)

which allows any type in the Eq class to be used as addresses of the fudgets to be combined. The restriction is that the fudgets combined must have the same type. (See Section 40.4 for a discussion of how a language with dependent types could eliminate this kind of restriction.)

There is also a combinator for untagged parallel composition:

>*< :: F i o -> F i o -> F i o

Input to an untagged parallel composition is sent to both argument fudgets.

There is a list version of untagged parallel composition as well,

untaggedListF :: [F a b] -> F a b

which can easily be defined using >*<:

untaggedListF = foldr (>*<) nullF

where nullF,

nullF :: F a b

is the fudget that ignores all input and never produces any output.

The untagged parallel compositions are not as widely used as the tagged ones. The reason is probably that you usually do not want input to be broadcast to all fudgets in a composition.

There are some further combinators that tend to be useful every once in a while. These are various parallel compositions with the identity fudget:

idRightF :: F a b -> F (Either a c) (Either b c)
idLeftF :: F a b -> F (Either c a) (Either c b)
bypassF :: F a a -> F a a
throughF :: F a b -> F a (Either b a)

idRightF  fud = fud >+< idF
idLeftF   fud = idF >+< fud
bypassF   fud = idF >*< fud
throughF  fud = idRightF fud >==< toBothF

toBothF :: F a (Either a a)
toBothF = concatMapF (\ x -> [Left x,Right x])

idF :: F a a
idF = mapF id

13.3 Loops

The simplest loop combinator is loopF,

loopF :: F a a -> F a a

In the composition loopF fud, the output from fud is not only output from the composition, but also sent back to the input of fud.

The most useful loop combinator is probably loopThroughRightF. An example use was shown in Section 9.7 and it is discussed further in Section 18.2.

Some loop combinators that have been useful are:

loopCompThroughRightF :: F (Either (Either a b) c) 
                           (Either (Either c d) a) -> F b d

loopCompThroughLeftF :: F (Either a (Either b c))
                          (Either b (Either a d)) -> F c d

These turn parallel compositions into loops. The following equations hold:

loopCompThroughRightF (l >+< r) = loopThroughRightF l r

loopCompThroughLeftF (l >+< r) = loopThroughRightF r l

13.4 Dynamic fudget creation

The combinators described in the previous sections can be used to build static networks of fudgets. The Fudget library also provides combinators that can be used to add or remove fudgets dynamically (for example, to create new windows dynamically).

To create dynamically changing parallel compositions of fudgets, the library provides

dynListF :: F (Int, DynFMsg a b) (Int, b)

where

data DynFMsg i o = DynCreate (F i o) | DynDestroy | DynMsg i

Above we saw listF that creates tagged parallel compositions that are static. The combinator dynListF can be seen as a variant of listF with a more elaborate input message type. When the program starts, dynListF is an empty parallel composition. A new fudget fud with address i can be added to the parallel composition by passing the message

(i,DynCreate fud)

to dynListF. The fudget with address i can be removed from the parallel composition by passing the message

(i,DynDestroy)

Finally, one can send a message x to an existing fudget with address i by passing the message

(i,DynMsg x)

to dynListF.

(The addresses used by dynListF have been restricted to the type Int for efficiency reasons, but in principle, more general address types could be supported, as for listF.)

A simpler combinator that allows fudgets to change dynamically is dynF:

dynF :: F a b -> F (Either (F a b) a) b

The fudget dynF fud starts out behaving like fud, except that messages to fud should be tagged with


      Right

. The fudget fud can be replaced by another fudget fud' by passing in the message Left fud'.

14 Fudgets for non-GUI I/O

14.1 Standard I/O fudgets

To read the standard input (usually the keyboard) and write to the standard output or standard error stream (the screen), you can use the fudgets:

stdinF   :: F a String
stdoutF  :: F String a
stderrF  :: F String a

The output from stdinF is the characters received from the program's standard input channel. For efficiency reasons, you do not get one character at a time, but larger chunks of characters. If you want the input as a stream of lines, you can use

inputLinesSP :: SP String String

which puts together the chunks and splits them at the newlines.

A simple example is a fudget that copies text from the keyboard to the screen with all letters converted to upper case:

stdoutF >==< (map toUpper >^=< stdinF)

It applies toUpper to all characters in the strings output by stdinF and then feeds the result to stdoutF.

Here is a fudget that reverses lines:

(stdoutF>=^<((++"\n").reverse))>==<(inputLinesSP>^^=<stdinF)

The precedences and associativities of the combinators are such that these fudgets can be written as:

stdoutF >==< map toUpper >^=< stdinF
stdoutF >=^< (++"\n").reverse >==< inputLinesSP >^^=< stdinF

14.2 Accessing the file system

The following fudgets allow you to read files, write files and get directory contents:

readFileF  :: F FilePath           (FilePath,Either IOError String)
writeFileF :: F (FilePath,String)  (FilePath,Either IOError ())
readDirF   :: F FilePath           (FilePath,Either IOError [FilePath])

These can be seen as servers, with a one-to-one correspondence between requests and responses. For convenience, the responses are paired with the file path from the request. The responses contain either an error message or the result of the request. The result is the contents of a file (readFile), a directory listing (readDirF), or () (


      writeFileF

14.3 The timer fudget

The timer fudget generates output after a certain delay and/or at regular time intervals. Its type is

data Tick = Tick
timerF :: F (Maybe (Int, Int)) Tick

The timer is initially idle. When it receives

Just
      (i,d)

on its input, it begins ticking. The first tick will be output after d milliseconds. Then, ticks will appear regularly at i millisecond intervals, unless i is 0, in which case only one tick will be output. Sending Nothing to the timer resets it to the idle state.

As a simple example, here is a fudget that outputs,once a second, the number of seconds that have elapsed since it was activated:

countSP >^^=< timerF >=^^< putSP (Just (1000,1000)) nullSP
  where countSP = mapAccumlSP inc 0
        inc n Tick = (n+1,n+1)

15 Parameters for customisation

When constructing software libraries, there may be a tension between simplicity and generality. Generality can be achieved by providing many parameters for adapting library components to different needs. But it ruins simplicity if the programmer has to specify a large number of parameters each time a library component is used. To solve this, some programming languages allow some of the arguments in a function call to be omitted, provided that default values are specified for them in the function definition. Haskell does not allow this, but by using one of the powers of functional languages, higher order functions, and the Haskell class system, something very similar can be achieved. The solution used in the Fudget library is presented below. Design and implementation issues are discussed in more detail in Chapter 30.

15.1 Customisers

In order to make fudgets easy to use in the common case and still flexible, they often come in two versions: a standard version, for example buttonF, and a customisable version, for example buttonF'. The name of the customisable version is obtained by appending a ' to the name of the standard version.

Customisable fudgets have a number of parameters that allow things like fonts, colors, border width, etc., to be specified. All these parameters have default values which are used in the standard version of the fudget.

Rather than having one extra argument for each such parameter, customisable versions of fudgets (or other functions) have one extra argument which is a customiser. The customiser is always the first argument. A customiser is a function that modifies a data structure containing the values of all parameters.

type Customiser a = a -> a

The type of the data structure is abstract. Its name is usually the name of the fudget, with the first letter change to upper case--for example, ButtonF in the case of buttonF'.

buttonF' :: (Graphic a) => 
            (Customiser (ButtonF a)) -> a -> F Click Click

So, customisers are obtained by composing a number of modifying functions using ordinary function composition. The function standard,

standard :: Customiser a

acts as the identity customiser and does not change any parameters. The standard versions of the fudgets are simply the customisable versions applied to standard, for example:

buttonF = buttonF' standard

15.2 Sample customisers

There are customisable versions of most fudgets presented earlier in this chapter.

The customisers that are common to many fudgets are overloaded. Some customiser classes are shown in Figure 23.

class HasBgColorSpec a  where setBgColorSpec  ::  ColorSpec -> Customiser a 
class HasFgColorSpec a  where setFgColorSpec  ::  ColorSpec -> Customiser a 
class HasFont a         where setFont         ::  FontName -> Customiser a 
class HasMargin a       where setMargin       ::  Int -> Customiser a 
class HasAlign a        where setAlign        ::  Alignment -> Customiser a 
class HasKeys a         where setKeys         ::  [(ModState, KeySym)] 
                                              ->  Customiser a 
...

Figure 23. Some customiser classes.

The table in Figure 24 shows what customisers are supported by the different customisable fudgets in the current version of the Fudget library.

BgColorSpec FgColorSpec Font Margin Align Keys
TextF y y y y y n
DisplayF y y y y y n
StringF y y y n n n
ButtonF y y y n n y
ToggleButtonF n n y n n y
RadioGroupF n n y n n n
ShellF n n n y n n
Figure 24. Some customiser instances.

Some fudgets also have non-overloaded customisers, for example:

setInitDisp :: a -> Customiser (DisplayF a)
-- changes what is displayed initially

setAllowedChar :: (Char -> Bool) -> Customiser StringF
-- changes what characters are allowed

setPlacer :: Placer -> Customiser RadioGroupF
-- changes the placements of the buttons

As an example of the use of customisation, Figure 25 shows a variation of the radio group shown in Figure 10.

radioGroupF' (setFont "fixed" . setPlacer (matrixP 2)) [(1,"P1"),(2,"P2"),(3,"P3"),(0,"Off")] 0
Figure 25. Custom version of the radio group in Figure 10.

III Stream processors -- the essence of Fudgets

The starting point of the work described in this thesis was the idea of the fudget as a process that communicates with other fudgets through the high-level streams and with the I/O system through the low-level streams. A fudget thus has two input streams and it is not known in advance in which order the elements in the two streams will become available. Fudgets should be able to listen to either the high-level input or the low-level input, but also choose to react to the first input to become available, irrespective of what stream it becomes available on. We expected that the former case would be the exception and the latter case would be the rule, so rather than providing some operator for indeterministic choice that the programmer could use in the definition of fudgets, we choose to merge the high- and low-level streams before feeding them to the fudget, thus moving the indeterministic choice outside the fudget.

So, we started out thinking of fudgets as the primitive concept, but soon saw them as being derived from a simpler concept, the stream processor, which is a process that communicates with its surroundings through a single input stream and a single output stream.

This part of the thesis is devoted to stream processors.

16 Stream processors

We have not used stream processors extensively in the examples presented so far, but plain stream processors are interesting for at least these reasons:

As suggested in Chapter 12, the application programmer can write the application-specific code in the form of stream processors.
As an application programmer, you usually abstract away from the low-level streams, and in fact handle fudgets as if they were plain stream processors with a single input and a single output stream. Hence, a lot of the discussion of stream processors applies to fudget application programming as well.
They are simpler than fudgets, but fudgets can be represented as stream processors. (We show how in Section 21.2.)
Stream processors can be used to structure an ordinary sequential Haskell program as a set of concurrent processes. Examples of this are shown in Chapter 19.

Viewed in a more general context, the stream processor can be seen as a simple but practical incarnation of the process concept, and has connections with process algebras such as CCS [Mil80]. An advantage with stream processors is that they admit a simple implementation within a purely functional language. We can define a set of combinators for building networks of stream processors, and the stream processors are first class values, which can be passed around as messages.

We use the following informal definitions:

A stream is a potentially infinite sequence of values occurring at different points in time. A stream can be seen as a communication channel, transferring information from one place (a producer) to another (a consumer).
A stream processor is a process which consumes some input streams and produces some output streams. A stream processor may have an internal state, i.e., output produced at a certain point in time can depend on all input consumed before that point in time.

These definitions allow stream processors to have many input and output streams, but in the following we will only consider stream processors with a single input stream and a single output stream (see Figure 26).

Figure 26. A general stream processor and a stream processor with a single input stream and a single output stream.

The restriction may seem severe, but the chosen set of combinators allows streams to be merged and split, so a stream processor with many input/output streams can be represented as one with a single input stream and a single output stream. The advantage is that we can take a combinator-based approach to building networks of communicating stream processors. The combinators are discussed further in Chapter 17. Below we discuss how to write atomic stream processors, that is, stream processors that do not consist of several concurrently running stream processors. Their behaviour is defined by a linear sequence of I/O actions.

16.1 The stream-processor type

The Fudget library provides an abstract type for stream processors,

data SP input output

where input and output are the types of the elements in the input and output streams, respectively (Figure 27). (The implementation of stream processors in a lazy functional language are discussed in Chapter 20.)

Figure 27. A stream processor of type SP i o.

The library also provides the function

runSP :: SP i o -> [i] -> [o]

which can be used on the top level of a program built with stream processors (see Chapter 19). The function absF discussed in Chapter 12 can be used to combine stream processors with fudgets.

16.2 Atomic stream processors in continuation style

The behaviour of an atomic stream processor is described by a sequential program. There are three basic actions a stream processor can take:

it can put a value in its output stream,
it can get a value from its input stream,
it can terminate.

The Fudget library provides the following continuation style operations for these actions:

putSP :: output -> SP input output -> SP input output
getSP :: (input -> SP input output) -> SP input output
nullSP :: SP input output

As an example of how to use these in recursive definitions of stream processors, consider the identity stream processor

-- The identity stream processor
idSP :: SP a a
idSP = getSP $ \ x -> putSP x idSP

the busy stream processor

-- A stream processor that is forever busy computing.
busySP :: SP a b
busySP = busySP

and the following stream-processor equivalents of the well known list functions:

mapSP :: (a -> b) -> SP a b
mapSP f = getSP $ \ x -> putSP (f x) $ mapSP f

filterSP :: (a -> Bool) -> SP a a
filterSP p = getSP $ \ x -> if p x
                            then putSP x $ filterSP p
                            else filterSP p

The stream processor nullSP need actually not be considered as a primitive. It can be defined as

nullSP = getSP $ \ x -> nullSP

i.e., it is a stream processor that ignores all input and never produces any output. A practical advantage with an explicitly represented nullSP is that it allows stream processors that terminate to be ``garbage collected''.

Example:

Implement concatMapSP :: (i->[o]) -> SP i o.

Solution:

First we define putListSP that outputs the elements of a list, one at a time:

putListSP :: [o] -> SP i o -> SP i o
putListSP [] = id
putListSP (x:xs) = putSP x . putListSP xs

And concatMapSP itself:

concatMapSP f =
    getSP $ \ x ->
    putListSP (f x) $
    concatMapSP f

Example:

Implement mapFilterSP :: (i->Maybe o) -> SP i o.

Solution:

mapFilterSP f =
        getSP $ \ x ->
        case f x of
          Nothing  -> mapFilterSP f
          Just y   -> putSP y $
                      mapFilterSP f

16.3 Stream processors with encapsulated state

A stream processor can maintain an internal state. In practice, this can be accomplished by using an accumulating argument in a recursively defined stream processor. As a concrete example, consider sumSP, a stream processor that computes the accumulated sum of its input stream:

sumSP :: Int -> SP Int Int
sumSP acc = getSP $ \ n -> putSP (acc+n) $ sumSP (acc+n)

In this case, the internal state is a value of the type Int, which also happens to be the type of the input and output streams. In general, the type of the input and output streams can be different from the type of the internal state, which can then be completely hidden.

The Fudget library provides two general functions for construction of stream processors with internal state:

mapAccumlSP        :: (s -> i -> (s, o)) -> s -> SP i o
concatMapAccumlSP  :: (s -> i -> (s, [o])) -> s -> SP i o

(concatMapAccumlSP is also known as mapstateSP.) The first argument to these functions is a state transition function which given the current state and an input message should produce a new state and an output message (zero or more outputs in the case of concatMapAccumlSP). Using mapAccumlSP we can define sumSP without using explicit recursion:

sumSP :: Int -> SP Int Int
sumSP = mapAccumlSP (\ acc n -> (acc+n,acc+n))

Representing state information as one or more accumulating arguments is useful when the behaviour of the stream processor is uniform with respect to the state. If a stream processor reacts differently to input depending on its current state, it can be more convenient to use a set of mutually recursive stream processors where each stream processor corresponds to a state in a finite state automaton. As a simple example, consider a stream processor that outputs every other element in its input stream:

passOnSP = getSP $ \ x -> putSP x $ skipSP
skipSP = getSP $ \ x -> passOnSP

It has two states: the ``pass on'' state, where the next input is passed on to the output; and the ``skip'' state, where the next input is skipped.

The two ways of representing state illustrated above, can of course be combined.

Example:

Implement mapAccumlSP and concatMapAccumlSP using putSP and getSP.

Solution:

concatMapAccumlSP :: (s -> i -> (s, [o])) -> s -> SP i o
concatMapAccumlSP f s0 =
    getSP $ \x ->
    let (s, ys) = f s0 x
    in putListSP ys $
       concatMapAccumlSP f s

mapAccumlSP :: (s -> i -> (s, o)) -> s -> SP i o
mapAccumlSP f s0 =
    getSP $ \x ->
    let (s, y) = f s0 x
    in putSP y $
       mapAccumlSP f s

16.4 Sequential composition of stream processors

Unlike CCS style process algebras [Mil80]--where nontrivial sequential behaviours can be constructed only by prefixing an existing behaviour with an I/O operation--the stream processors can be combined sequentially:

seqSP :: SP a b -> SP a b -> SP a b

The stream processor sp₁ `seqSP` sp₂ behaves like sp₁ until sp₁ becomes nullSP, and then behaves like sp₂. However, the same can also be achieved by making all procedures end with a call to a continuation stream processor instead of nullSP; so seqSP does not add any new power.

We should also note that if this is to work properly, the operation nullSP must be explicitly represented, and not just defined as a stream processor that ignores all input and never produces any output; contrary to what was suggested in Section 16.2.

16.5 Stream-processor monads

The presentation thus far suggests that atomic stream processors should be programmed in continuation style. This is often natural, but for complex stream processors it can be beneficial to use a monadic style instead [Wad92,Wad95]. The two styles are compatible. The operations of the stream processor monad are shown in Figure 28.

-- The type:
type SPm input output answer

-- Standard monad operations:
unitSPm :: a -> SPm i o a
bindSPm :: SPm i o a -> (a -> SPm i o b) -> SPm i o b

-- Monadic versions of nullSP, putSP and getSP:
nullSPm :: SPm i o ()
putSPm  :: o -> SPm i o ()
getSPm  :: SPm i o i

-- A glue function:
runSPm  :: SPm i o () -> SP i o

Figure 28. The stream-processor monad.

Thanks to runSPm you can use the combinators for ``plain'' stream processors to construct networks of stream-processor monads.

For writing complex stream processors, it is of course possible to combine the stream-processor monad with other monads, e.g., a state monad. The Fudget library defines the type SPms for stream processor-monads with state. A closer presentation and an example of its use can be found as part of Chapter 31.

17 Plumbing: composing stream processors

This section describes the combinators used to combine atomic stream processors into networks of communicating stream processors. We first describe combinators for the three basic compositions: serial composition, parallel composition and loops.

17.1 Serial composition

The simplest combinator is the one for serial composition,

(-==-) :: SP b c -> SP a b -> SP a c

It connects the output stream of one stream processor to the input stream of another, as illustrated in Figure 29. Streams flow from right to left, just like values in function compositions, f . g.

Figure 29. Serial composition of stream processors.

Serial composition of stream processors is very close to function composition. For example, it obeys the following law:

mapSP f -==- mapSP g = mapSP (f . g)

17.2 Parallel compositions

The combinator for parallel composition in Figure 30 is indeed the key combinator for stream processors. It allows us to write reactive programs composed by more or less independent, parallel processes. The output streams should be merged in chronological order. We will not be able to achieve exactly this in a functional language, but for stream processors whose behaviour is dominated by I/O operations rather than internal computations, we will get close enough for practical purposes.

Figure 30. Parallel composition of stream processors.

There is however, more than one possible definition of parallel composition. How should values in the input stream be distributed to the two stream processors? How should the output streams be merged? We define two versions:

Let sp₁ -*- sp₂ denote parallel composition where input values are propagated to both sp₁ and sp₂, and output is merged in chronological order. We will call this version untagged, or broadcasting parallel composition.
Let sp₁ -+- sp₂ denote parallel composition where the values of the input and output streams are elements of a disjoint union. Values in the input stream tagged Left or Right are untagged and sent to either sp₁ or sp₂, respectively. Likewise, the tag of a value in the output stream indicates which component it came from. We will call this version tagged parallel composition.

The types of the two combinators are:

(-*-) :: SP i o -> SP i o -> SP i o
(-+-) :: SP i1 o1 -> SP i2 o2 -> SP (Either i1 i2) (Either o1 o2)

Note that only one of these needs to be considered as primitive. The other can be defined in terms of the primitive one, with the help of serial composition and some simple stream processors like mapSP and filterSP.

Example:

Define -*- in terms of -+-, and vice versa.

Solution:

(-*-) :: SP i o -> SP i o -> SP i o
sp1 -*- sp2 =
        mapSP stripEither -==-
        (sp1 -+- sp2) -==-
        toBothSP

stripEither :: Either a a -> a
stripEither (Left a)   = a
stripEither (Right a)  = a

toBothSP :: SP a (Either a a)
toBothSP = concatMapSP (\x -> [Left x, Right x])

(-+-) :: SP i1 o1 -> SP i2 o2 -> SP (Either i1 i2) (Either o1 o2)
sp1 -+- sp2 = sp1' -*- sp2'
  where
    sp1' = mapSP Left  -==- sp1 -==- filterLeftSP
    sp2' = mapSP Right -==- sp2 -==- filterRightSP

filterLeftSP  = mapFilterSP stripLeft
filterRightSP = mapFilterSP stripRight

stripLeft :: Either a b -> Maybe a
stripLeft (Left x)   = Just x
stripLeft (Right _)  = Nothing
stripRight :: Either a b -> Maybe b
stripRight (Left _)   = Nothing
stripRight (Right y)  = Just y

17.3 Circular connections

Serial composition creates a unidirectional communication channel between two stream processors. Parallel composition splits and merges streams but does not allow the composed stream processors to exchange information. So, with these two operators we cannot obtain bidirectional communication between stream processors. Therefore, we introduce combinators that construct loops.

The simplest possible loop combinator connects the output of a stream processor to its input, as illustrated in Figure 31. As with parallel composition, we define two versions of the loop combinator:

Figure 31. A simple loop constructor.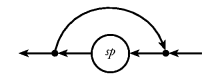

loopSP sp,: output from sp is both looped to the input of sp and propagated to the output, outside the loop.
loopLeftSP sp,: output from sp is required to be in a disjoint union. Values tagged Left are looped and values tagged Right are output. At the input, values from the loop are tagged Left and values from the outside are tagged Right.

The types of these combinators are:

loopSP :: SP a a -> SP a a
loopLeftSP :: SP (Either l i) (Either l o) -> SP i o

Each of the two loop combinators can be defined in terms of the other, so only one of them needs to be considered primitive.

Using one of the loop combinators, one can now obtain bidirectional communication between two stream processors as shown in Figure 32.

Figure 32. Using a loop to obtain bidirectional communication.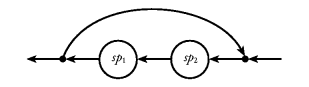

Another example shows that we can use loops and parallel composition to create fully connected networks of stream processors. With an expression like

loopSP (sp₁ -*- sp₂ -*- ... -*- sp_n)

we get a broadcasting network. By replacing -*- with -+- and some tagging/untagging, we get a network with point-to-point communication.

Example:

Define loopSP in terms of loopLeftSP and vice versa.

Solution:

Defining loopSP in terms of loopLeftSP is relatively easy:

loopSP :: SP a a -> SP a a
loopSP sp =
        loopLeftSP
          (toBothSP -==- sp -==- mapSP stripEither)

Vice versa is a bit trickier:

loopLeftSP :: SP (Either l i) (Either l o) -> SP i o
loopLeftSP sp =
    mapFilterSP post -==-
    loopSP sp' -==-
    mapSP Right
  where
    post (Left (Right x)) = Just x
    post _ = Nothing
    sp' = mapSP Left -==- sp -==- mapFilterSP pre
      where
        pre (Right x) = Just (Right x)
        pre (Left (Left x)) = Just (Left x)
        pre _ = Nothing

18 Pragmatic aspects of plumbing

Having seen a basic set of stream-processor combinators--which we can consider as a complete set of primitives on top of which further combinators can be built--we now take a look at how the combinators can be used to achieve some common connection patterns and introduces some further combinators we have found useful.

Fudgets are composed in the same way as plain stream processors. Therefore, the description of the stream-processor combinators also holds true for the corresponding fudget combinators. The fudget combinators are presented by name, together with some further combinators, in Chapter 13.

18.1 Handling multiple input and output streams

Although stream processors have only one input stream, it is easy to construct programs where one stream processor receives input from two or more other stream processors. (The case with several outputs is analogous.) For example, the expression

sp₁ -==- (sp₂ -+- sp₃)

allows sp₁ to receive input from both sp₂ and sp₃. For most practical purposes, sp₁ can be regarded as having two input streams, as illustrated in Figure 33. When you use getSP in sp₁ to read from the input streams, messages from sp₂ and sp₃ will appear tagged with Left and Right, respectively. You can not directly read selectively from one of the two input streams, but the Fudget library provides the combinator

Figure 33. Handling multiple input streams.

waitForSP :: (i -> Maybe i') -> (i' -> SP i o) -> SP i o

which you can use to wait for a selected input. Other input is queued and can be consumed after the selected input has been received. Using waitForSP you can define combinators to read from one of two input streams:

getLeftSP :: (i1 -> SP (Either i1 i2) o) -> SP (Either i1 i2) o
getLeftSP = waitForSP stripLeft
getRightSP :: (i2 -> SP (Either i1 i2) o) -> SP (Either i1 i2) o
getRightSP = waitForSP stripRight

Example:

Implement startupSP :: [i] -> SP i o -> SP i o that prepends some elements to the input stream of a stream processor.

Solution:

startupSP xs sp = sp -==- putListSP xs idSP

Note: this implementation leaves a serial composition with idSP behind after the messages xs have been fed to sp. An efficient implementation that does not leave any overhead behind can be obtained by making use of the actual representation of stream processors.

Example:

Implement waitForSP described above.

Solution:

waitForSP :: (i -> Maybe i') -> (i' -> SP i o) -> SP i o
waitForSP expected isp =
    let contSP pending =
          getSP $ \ msg ->
          case expected msg of
            Just answer  -> startupSP (reverse pending) (isp answer)
            Nothing      -> contSP (msg : pending)

    in  contSP []

18.2 Stream processors and software reuse

For serious applications programming, it is useful to have libraries of reusable software components. But in many cases when a useful component is found in a library, it still needs modification before it can be used.

A variation of the loop combinators that has turned out to be very useful when reusing stream processors is loopThroughRightSP, illustrated in Figure 34. The key difference from loopSP and loopLeftSP is that the loop does not go directly back from the output to the input of a single stream processor. Instead it goes through another stream processor.

Figure 34. Encapsulation.

A typical situation where 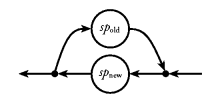loopThroughRightSP is useful is when you have a stream processor, sp_old, that does almost what you want it to do, but you need it to handle some new kind of messages. A new stream processor, sp_new, can then be defined. This new stream processor can pass on old messages directly to sp_old and handle the new messages in the appropriate way; on its own, or by translating them to messages that sp_old understands. (See also Section 3.1.1 in [NR94].)

In the composition loopThroughRightSP sp_new sp_old, all communication with the outside world is handled by sp_new. sp_old is connected only to sp_new, and is in this sense encapsulated inside sp_new.

The type of loopThroughRightSP is:

loopThroughRightSP :: SP (Either oldo newi) (Either oldi newo) -> 
                      SP oldi oldo -> 
                      SP newi newo

Programming with loopThroughRightSP corresponds to inheritance in object-oriented programming. The encapsulated stream processor corresponds to the inherited class. Overridden methods correspond to message constructors that the encapsulating stream processor handles itself.

Example:

Implement loopThroughRightSP using


            loopLeftSP

together with parallel and serial compositions as appropriate.

Solution:

loopThroughRightSP ::
  SP (Either oldo i) (Either oldi o) -> SP oldi oldo ->SP i o
loopThroughRightSP spnew spold =
    loopLeftSP
      (mapSP post  -==- (spold -+- spnew)
                   -==- mapSP pre)
  where
    pre (Right input) = Right (Right input)
    pre (Left (Left newToOld)) = Left newToOld
    pre (Left (Right oldToNew)) = Right (Left oldToNew)
    post (Right (Right output)) = Right output
    post (Right (Left newToOld)) = Left (Left newToOld)
    post (Left oldToNew) = Left (Right oldToNew)

Example:

Implement serial composition using a tagged parallel composition and a loop.

Solution:

(-==-) :: SP b c -> SP a b -> SP a c
sp1 -==- sp2 =
    loopThroughRightSP (mapSP route) (sp1 -+- sp2)
  where
    route (Right a) = Left (Right a)
    route (Left (Left c)) = Right c
    route (Left (Right b)) = Left (Left b)

The combinator loopThroughBothSP,

loopThroughBothSP  ::     SP (Either l12 i1) (Either l21 o1)
                      ->  SP (Either l21 i2) (Either l12 o2)
                      ->  SP (Either i1  i2) (Either o1  o2)

is a symmetric version of loopThroughRightSP. A composition loopThroughBothSP sp₁ sp₂ allows both sp₁ and sp₂ to communicate with the outside world and with each other (see Figure 35).

Figure 35. Circuit diagram for loopThroughBothSP.

An interesting property of loopThroughBothSP is that the circuit diagrams of the more basic combinators, -==-, -+- and loopSP, can be obtained from the circuit diagram of loopThroughBothSP by just removing wires. Other combinators are thus easy to define in terms of loopThroughBothSP.

18.3 Dynamic process creation

We implicitly made a distinction between the operators that define the dynamic behaviour of an atomic stream processors (nullSP, putSP and getSP) and the operators that are used to build static networks of stream processors (-==-, -*-, loopSP, etc.). But there is in fact no reason why networks must be static. By using combinators like -==- and -*- in a dynamic way, the number of stream processors can be made to increase dynamically. The number of stream processors can also decrease, for example if a component of a parallel composition dies (since nullSP -*- sp is equivalent to sp).

A practical application of these ideas is discussed in Section 35.4.

19 Application programming with plain stream processors

Although plain stream processors are mostly used in conjunction with fudgets, they can be used independently. In this chapter, we take a look at some examples of interactive Haskell programs written using stream processors.

19.1 An adding machine

In Section 16.3 we defined

sumSP :: Int -> SP Int Int

that computes the accumulating sum of a stream of integers. Let us write a complete Haskell program that uses sumSP to implement a simple adding machine.

Haskell provides the function interact, which allows functions of type [Char] -> [Char] to be used as programs (as in Landin's stream I/O model outlined in Chapter 4). By combining this with the function runSP,

runSP :: SP i o -> [i] -> [o]

(from Section 16.1) we can run stream processors of type

SP
        Char Char

main = interact (runSP mainSP)
mainSP :: SP Char Char
mainSP = ...

To be able to use sumSP we need only add some glue functions that convert the input stream of characters to a stream of numbers and conversely for the output stream. This is done in two stages. First, the stream-processor equivalents of the standard list functions lines and unlines are used to process input and output line by line, instead of character by character:

mainSP = unlinesSP -==- adderSP -==- linesSP
adderSP :: SP String String
adderSP = ...

Now the standard functions show and read are used to convert between strings and numbers,

adderSP = mapSP show -==- sumSP 0 -==- mapSP read

and the program is complete.

Example:

Implement unlinesSP :: SP String Char.

Solution:

unlinesSP = concatMapSP (\s -> s++"\n")

Example:

Implement linesSP :: SP Char String

Solution:

linesSP = lnSP []
  where
    lnSP acc =
      getSP $ \msg ->
      case msg of
        '\n'  -> putSP (reverse acc) (lnSP [])
        c     -> lnSP (c : acc)

19.2 A stream processor for input line editing

In the example above, it was assumed that input is line buffered (cooked terminal mode in Unix), i.e., the system allows the user to enter a line of text and edit it by using the backspace key, (and possibly other cursor motion keys) and send it to the program by pressing the Return key. The system is thus responsible for echoing characters typed on the keyboard, to the screen (Figure 36).

Figure 36. Line buffered input.

Assuming a simpler system, where keyboard input is fed directly to the program, and the only characters shown on the screen are those output by the program (raw terminal mode in Unix) (Figure 37), the stream-processor combinator lineBufferSP is now defined to do the job:

Figure 37. Unbuffered input.

lineBufferSP :: SP String Char -> SP Char Char

It takes a stream processor that expects the input to be line buffered, and returns a stream processor that does the necessary processing of the input: buffering, echoing, etc., so that it can work in an unbuffered environment.

We implement lineBufferSP using loopThroughRightSP:

lineBufferSP progsp = loopThroughRightSP bufSP progsp
  where
    bufSP :: SP (Either Char Char) (Either String Char)
    bufSP = ...

We get the connectivity shown in Figure 38, i.e., bufSP will receive program output and keyboard input on its input stream and should produce input lines and screen output on its output stream.

Figure 38. Circuit diagram for lineBufferSP.

The implementation of bufSP is shown in Figure 39.

bufSP = inputSP ""

inputSP line = getSP $ either fromProgsp fromKeyboard
  where
    fromProgsp c = putSP (toScreen c) (inputSP line)

    fromKeyboard c =
      case c of
        -- The Enter key:
        '\n' -> putSP (toScreen '\n') $
                putSP (toProgsp (reverse line)) $
                bufSP
        -- The backspace key:
        '\b' -> if null line
                then inputSP line
                else putsSP (map toScreen "\b \b") $
                     inputSP (tail line)
        -- Printable characters:
        _    -> putSP (toScreen c) $
                inputSP (c:line)

    toScreen = Right
    toProgsp = Left

Figure 39. bufSP - the core of lineBufferSP.

Using lineBufferSP, the adding machine in the previous section can be adapted to run in raw terminal mode by change mainSP to:

mainSP = lineBufferSP (unlinesSP -==- adderSP)

19.3 Running two programs in parallel on a split screen

This last example is a combinator that splits the terminal screen into two windows and runs two programs in parallel, one in each window:

splitViewSP :: SP Char Char -> SP Char Char -> SP Char Char

A simple implementation of splitViewSP can be structured as follows:

splitViewSP sp1 sp2 =
        mergeSP -==- (sp1 -+- sp2) -==- distrSP
  where
        distrSP :: SP Char (Either Char Char)
        distrSP = ...
        mergeSP :: SP (Either Char Char) Char
        mergeSP = ...

distrSP takes the keyboard input and sends it to one of the two windows. The user can switch windows by pressing a designated key.

mergeSP takes the two output streams from the windows and produces a merged stream, which contains the appropriate cursor control sequences to make the text appear in the right places on the screen. This can be done in different ways depending on the terminal characteristics. A simple solution, if scrolling is not required, is to split the processing into two steps: the first being to interpret the output streams from the two windows individually to keep track of the current cursor position using a stream processor like

trackCursorSP :: SP Char ((Int,Int),Char)

It takes a character stream containing a mixture of printable characters and cursor control characters, and produces a stream with pairs of cursor positions and printable characters. The next step is to merge the two streams and feed them into a stream processor that generates the appropriate cursor motion commands for the terminal:

encodeCursorMotionSP :: SP ((Int,Int),Char) Char

Thus we have

mergeSP =
        encodeCursorMotionSP -==-
        mapSP stripEither -==-
        (trackCursorSP -+- trackCursorSP)

Using the above outlined implementation of mergeSP, we get the circuit diagram shown in Figure 40 for splitViewSP sp₁ sp₂:

Figure 40. Circuit diagram for splitViewSP sp₁ sp₂.

Filling in some details we ignored in the above description, we get the implementation shown in Figure 41.

splitViewSP :: (Int,Int) -> SP Char Char -> SP Char Char -> SP Char Char
splitViewSP (w,h) sp1 sp2 =
  mergeSP -==- (sp1 -+- sp2) -==- distrSP Left Right
where
  mergeSP = encodeCursorMotionSP -==-
            mapSP stripEither -==-
                (trackCursorSP (w,h1) -+-
                 (mapSP movey -==- trackCursorSP (w,h2)))

  h1 = (h-1) `div` 2
  h2 = h-1-h1

  movey ((x,y),c) = ((x,y+h1+1),c)

  distrSP dst1 dst2 =
    getSP $ \ c ->
    case c of
      '\t' -> distrSP dst2 dst1
      _    -> putSP (dst1 c) $ distrSP dst1 dst2

trackCursorSP :: (Int,Int) -> SP Char ((Int,Int),Char)
trackCursorSP size = mapstateSP winpos (0,0)
  where winpos p c = (nextpos p c,[(p,c)])

encodeCursorMotionSP :: SP ((Int,Int),Char) Char
encodeCursorMotionSP = mapstateSP term (-1,-1)
  where
    term cur@(curx,cury) (p@(x,y),c) =
        (nextpos p c,move++[c])
      where
        move = if p==cur
               then ""
               else moveTo p

nextpos :: (Int,Int) -> Char -> (Int,Int)
nextpos p c = ... -- cursor position after c has been printed

moveTo :: (Int,Int) -> String
moveTo (x,y) = ... -- generate the appropriate cursor control sequence

Figure 41. An implementation of splitViewSP.

IV Design and implementation

In this part, we will describe the design and implementation of the Fudget library itself, as well as some extensions we have done. The organisation of the first chapters can be summarised in the words the library, extensions and programming methods:

The library.

These chapters describe the fundamental principles behind the Fudget library. Chapter 20 discusses different implementations of stream processors. The implementation of the fudget combinators is based on stream processors, and allows them to communicate with different kind of I/O systems (Chapter 21). Chapter 22 describes the mechanism behind the GUI fudgets, asynchronous I/O and the low-level interfaces to X Windows.

The automatic layout system in Chapter 23 can be seen as a sub-library of combinators, which is used not only for placing the GUI fudgets, but also to compose graphics.

Two examples of filter fudgets (combinators that modify the effect of fudgets) are presented in Chapter 24. The cache filter makes fudget programs run faster using less memory, and the focus filter modifies the input model of GUI fudgets that use the keyboard.

Extensions.

The next chapters describe extensions that we do not consider absolutely essential for the library, although some of them reside in the library itself, and others have at least prompted modification of the library in order to work.

A distinguishing feature of stream processors and fudgets is that they can be detached from their original position in the program, passed as messages, and attached at another position. Chapter 25 describes how this can be used to program drag-and-drop applications, where GUI fudgets actually move inside the program when dragged.

Chapter 26 shows how the fudget concept can be used for programming client/server applications. Server programs do usually not have any graphical interface, but it is can be advantageous to program servers in a concurrent style so that they can serve many clients simultaneously.

The library contains a class of types that has a graphical appearance, which can be manipulated by the user. Chapter 27 presents the Graphic class and its implementation.

Programming methods.

These chapters describe our experiments in programming methods using Fudgets. Chapter 28 describes combinators for creating syntax-oriented editors in a style similar to parsing combinators, and Chapter 29 shows how Haskell's class system can be used to automatically generate simple GUIs. As we have already seen in the previous part, the class system has also been used to program functions that use named parameters with default values. The implementation is described in Chapter 30.

Finally, Chapter 31 describes an implementation of the functional toolkit Gadgets on top of the Fudget library. This includes a functional implementation of the process concept in Gadgets, and allows Gadget programs to be incorporated in Fudgets. As a bonus, a profiling utility was added which provides a graphical monitor of the message queues.

20 Implementing stream processors

In this chapter we present different implementations of stream processors, including a indeterministic solution that requires a language extension for parallel evaluation, and two purely functional ones: the first is based on streams as lazy lists, and the other uses a datatype with constructors corresponding to the operations of atomic stream processors We also discuss how suitable different representations are for parallel and sequential implementations. We start by discussing some design goals that we had in mind.

20.1 Design goals for stream processors

The design of the stream processors was already from the start influenced by the intended application as building blocks in a GUI library. In this context, we found the following properties important:

Hierarchical structure.: The result of a composition of stream processors should also be a stream processor, thus allowing complex process networks to be built in an hierarchical structure. There should be no difference in principle between an atomic stream processor and one composed from several smaller stream processors.
Encapsulated state.: We should permit each stream processor to have an internal state which is invisible from the outside, and which does not interfere with the state of other stream processors.
I/O connectedness.: It should be possible to connect stream processors to the I/O system in an abstract way, so that the I/O effects can be hidden by an abstract type with associated combinators for their combination.
Reactive behaviour.: The intended use of stream processors is in the implementation of interactive (reactive) programs. This means that programs are dominated by communication rather than computation: a program waits idly for some input to arrive, computes and outputs a response to the input, and then goes back to the idle state.
Demand-driven evaluation.: The intention is to use stream processors in a lazy functional language, where expressions are evaluated on demand. Stream processors should also behave lazily--they should not do any work until a value is demanded from their output stream, and they should not demand anything from their input stream unless the input can be used to produce a demanded output.
Typed, and higher order.: There should be no restriction on the element type of streams. It should be possible to transfer anything, from numbers and booleans to functions and stream processors. Communication should be type safe.
Parallel and sequential implementations.: Stream processors should be implementable in a sequential language, but we still want to keep the definitions general enough to be able to take advantage of constructions for indeterministic choices and parallel evaluation.

Especially in the light of the last property, it seems desirable to have an abstract, formal semantics which can be used to reason about different implementations of stream processors, and programs using them. So far, we have not elaborated such a semantics, but instead we have concentrated on more practical work by developing the Fudget library and application programs. Moreover, the implementation of the basic stream-processor combinators is quite simple, and can therefore be viewed as being a semantics on its own--although not the most concise and abstract one could imagine. Nevertheless, we have outlined a simple stream-processor calculus with an accompanying operational semantics in the future work chapter (see Section 43.1).

20.2 Intuitive ideas--what is the problem?

In a lazy functional language, a natural choice is to represent streams as lists. Thanks to laziness, the elements of the list can be computed on demand, one element at a time. The elements can thus form a sequence in time rather than a sequence in space, which would be the case in a strict language.

So a stream with elements of type a can be represented as a list with elements of type a. A stream processor can be represented as function from the input stream to the output stream:

type Stream a = [a]
type SP i o = Stream i -> Stream o

We call this the list-based representation. An obvious advantage with this approach is that the list type is a standard type and all operations provided for lists can be reused when defining stream processors.

Another advantage with this representation is that it clearly shows the close relationship between functions and stream processors. For example, serial composition is simply function composition:

(-==-) :: SP m o -> SP i m -> SP i o
sp1 -==- sp2 = sp1 . sp2

The basic stream processor actions also have very simple definitions:

nullSP        = \ xs -> []
x `putSP` sp  = \ xs -> x : sp xs
getSP isp     = \ xs -> case xs of
                           []     -> []
                           x:xs'  -> isp x xs'

A problem with this representation however, is that parallel composition is impossible to implement. A reasonable definition would have to look something like this:

sp1 -*- sp2 = \ xs -> merge (sp1 xs) (sp2 xs)
     where merge ys zs = ???

But what should ??? be replaced with, so that the first output from the composition is the first output to become available from one of the components? For example, suppose that

sp₁ _|_ = _|_
sp₂ _|_ = 1:_|_

that is, sp₁ needs some input before it can produce some output, but sp₂ can output 1 immediately. Then, the composition should immediately output 1,

(sp₁ -*- sp₂) _|_ = 1:_|_

But (sp₂ -*- sp₁) _|_ should also be 1:_|_, so ??? must be an expression that chooses the one of

ys

and zs which happens to be non-bottom. This can clearly not be done in an ordinary purely functional language.

As a more concrete example, consider what should happen if we apply the stream processor

map (*100) -*- filter even

to [1, 2, 3, 4, ...]. If the input elements appear at a slower rate than they can be processed by either map or filter, the desired output stream would be something like

[100, 200, 2, 300,
      4, 400, ...]

, i.e., in this particular case there should be two elements from the left stream processor for every element from the right stream processor.

The elements in the two output streams should be merged in the order they become computable as more elements of the input stream become available. However, there is no way of telling in a sequential language which of the two stream processors will be the first one to be able to produce an output. Is seems that the two streams need to be evaluated in parallel, and then elements must be chosen in the order they become available.

The most natural and general solution to this problem is to use parallel evaluation, and we will take a look at this next. But by changing the representation of stream processors it is possible to obtain solutions that work in an ordinary sequential language. We will look at these solutions in Section 20.4.

20.3 Parallel implementations

As illustrated in the previous section, when representing stream processors as list functions, parallel evaluation is needed, not to gain speed, but because no sequential evaluation order can give the desired result. We need an operator that starts the evaluation of two subexpressions in parallel, and then tells which evaluation finished first. The result is thus not determined by the values of the expressions, but rather from their operational behaviour. Therefore, such an operator cannot be added to a purely functional language without problems.

The operator suggested above is a variant of amb, McCarthy's ambivalent operator [McC63]. But a programming language with such an operator is not purely functional, and thus makes ordinary equational reasoning unsound. Although such a language may still be useful [Mor94], there are solutions that allow you to make indeterministic choices in a purely functional way.

In the following section, we will introduce a variant of amb which is purely functional.

20.3.1 Oracles

To be purely functional, the result of an operator must depend entirely on the values of the arguments, and the same arguments should always give the same result. One way to make an operator for indeterministic choice purely functional is to introduce an extra argument and pretend that the result is determined solely by this argument, although operationally, something else happens. Such an extra argument is called an oracle [Bur88].

We call our operator for indeterministic choice choose:

choose :: Oracle -> a -> b -> Bool

Operationally, the expression

choose o a
        b

is evaluated by starting the evaluation of a and b in parallel and then returning True if a reaches head normal form first, and False if b does. Denotationally,

choose o a
        b

returns True or False depending only on the value of the oracle o (which magically happen to have the ``right'' value). An oracle should only be used once, since it must always give the same answer. We therefore distribute an infinite tree of oracles to all stream processors, as an additional argument:

data OracleTree = OracleNode OracleTree Oracle OracleTree
type SP i o = OracleTree -> Stream i -> Stream o

Using the oracle tree, we can now easily implement parallel composition of stream processors (see also Figure 42):

sp1 -*- sp2 =
        \(OracleNode (OracleNode ot _ ot1) _ ot2) xs ->
            merge ot (sp1 ot1 xs) (sp2 ot2 xs)
  where merge (OracleNode ot o _) ys zs =
          if choose o ys zs
          then merge' ot ys zs
          else merge' ot zs ys
        merge' ot (y:ys)  zs = y:merge ot ys zs
        merge' ot []      zs = zs

In this implementation, the oracle tree is split into three: two subtrees are fed to the composed stream processors, and one is given to the function merge, together with the output streams from the composed stream processors. The function merge extracts fresh oracles from the tree and uses choose to see which stream is first to reach head normal form, It then calls merge', with the second argument being the stream which has been evaluated.

Figure 42. Parallel composition of stream processors using oracles.

20.4 Sequential implementations

As we have seen above, the most natural representation of streams, i.e., as lists, requires parallel evaluation and indeterministic choices. But there are solutions that allow you to stay within a purely functional language, like Haskell. Although they do not provide the same degree of parallelism, they have proved to be adequate for practical use. The solutions below have been used in the implementation of the Fudget system.

20.4.1 Synthetic oracles

As seen in Section 20.2, the problem with the most natural representation of stream processors--representing streams as lazy lists and stream processors as functions on lazy lists--is the implementation of parallel composition. It is impossible to know in which order the output streams should be merged.

If we impose the restriction that sp₁ and sp₂ must produce output at the same rate, then sp₁ -*- sp₂ can be defined as:

(sp1 -*- sp2) xs = merge (sp1 xs) (sp2 xs)
   where merge (y:ys) (z:zs) = y:z:merge ys zs

However, it is awkward to impose such a constraint between the output streams of two different stream processors. Also, this solution does not work well for tagged parallel composition. A more useful constraint relates the input and output stream of a single stream processor.

We impose the constraint that there must be a one-to-one correspondence between elements in the output and the input stream, i.e., a stream processor must put one element in the output stream for every element consumed from the input stream.

The function map is an example that satisfies this constraint, whereas filter is a function that does not.

With this restriction, tagged parallel composition can easily be implemented: the next element in the output stream should be taken from the stream processor that last received an element from the input stream. The following implementation of tagged parallel composition uses this fact by merging the output streams using a stream of synthetic oracles computed from the input stream (see also Figure 43):

(-+-) :: SP a1 b1 -> SP a2 b2 -> SP (Either a1 a2) (Either b1 b2)
(sp1 -+- sp2) xs = merge os (sp1 xs1) (sp2 xs2)
  where
    xs1 = [ x | Left x <- xs ]
    xs2 = [ y | Right y <- xs ]
    -- os : a synthetic oracle stream
    os  = map isLeft xs
    merge (True:os) (y:ys) zs =
           Left y:merge os ys zs
    merge (False:os) ys (z:zs) =
           Right z:merge os ys zs
    isLeft (Left   _) = True
    isLeft (Right  _) = False

Figure 43. Parallel composition of stream processors using synthetic oracles.

This solution has some practical problems, however. As it stands above, there is a potentially serious space-leak problem. Consider the evaluation of an expression like

(sp₁ -+- sp₂) [Left n | n<-[1..]]

Here, sp₂ will never receive any input. This means that merge will never need to evaluate the argument


        (sp₂ xs2)

, which holds a reference to the beginning of the input stream via xs2. This would cause all input consumed by the composition to be retained in the heap. However, provided that pattern bindings are implemented properly [Spa93], this problem can be solved by computing

xs1

and xs2 with a single recursive definition that returns a pair of lists:

split :: [Either a b] -> ([a],[b])
split [] = ([],[])
split (x:xs) =
    case x of
      Left   x1  -> (x1:xs1,xs2)
      Right  x2  -> (xs1,x2:xs2)
  where
    (xs1,xs2) = split xs

Another problem is that the 1-1 restriction is rather severe. What should a stream processor do if it does not want to put a value in the output stream after consuming an input (like filter)? What if it wants to output more than one value? Obviously, if an implementation with this restriction is given to a programmer, he will invent various ways to get around it. It is better to provide a solution from the beginning.

One way to relieve the restriction is to change the representation of stream processors to

type SP a b = [a] -> [[b]]

thus allowing a stream processor to output a list of values to put in the output stream for every element in the input stream. Unfortunately, with this representation the standard list functions, like map and filter, can no longer be used in such a direct way. For example, instead of map f one must use map (\x->[f x]). Serial composition is no longer just function composition, rather it is something more complicated and less efficient. Also, it is still possible to write stream processors that do not obey the 1-1 restriction, leading to errors that can not be detected by a compiler. Consequently, it is not a good idea to reveal this representation to the application programmer, but rather provide the stream-processor type as an abstract type. And while we are using an abstract type, we might as well use a better representation.

20.4.2 Continuation-based representation

Instead of using lists, the Fudget library uses a data type with constructors corresponding to the actions a stream processor can take (as described in Section 3.2):

data SP i o
  =  NullSP     
  |  PutSP o (SP i o)
  |  GetSP (i -> SP i o)

We call this the continuation-based representation of stream processors. The type has one constructor for each operation a stream processor can perform. The constructors have arguments that are part of the operations (the value to output in PutSP), and arguments that determine how the stream processor continues after the operation has been performed.

The continuation-based representation avoids the problem with parallel composition that we ran into when using the list-based representation, since it makes the consumption of the input stream observable. With list functions, a stream processor is applied to the entire input stream once and for all. The rate at which elements are consumed in this list is not observable from the outside. With the continuation-based representation, a stream processor must evaluate to GetSP sp each time it wants to read a value from the input stream. This is what we need to be able to merge the output stream in the right order in the definition of parallel composition.

An implementation of broadcasting parallel composition is shown in Figure 44. The implementation of tagged parallel composition is analogous. Note that we arbitrarily choose to inspect the left argument sp₁ first. This means that even if sp₂ could compute and output a value much faster than sp₁, it will not get the chance to do so.

NullSP        -*- sp2           = sp2
sp1           -*- NullSP        = sp1
PutSP o sp1'  -*- sp2           = PutSP o (sp1' -*- sp2)
sp1           -*- PutSP o sp2'  = PutSP o (sp1 -*- sp2')
GetSP xsp1    -*- GetSP xsp2    = GetSP (\i -> xsp1 i -*- xsp2 i)

Figure 44. Implementation of parallel composition with the continuation-based representation.

With the continuation-based representation, serial composition can be implemented as shown in Figure 45.

NullSP        -==- sp2           = NullSP
PutSP o sp1'  -==- sp2           = PutSP o (sp1' -==- sp2)
GetSP xsp1    -==- NullSP        = NullSP
GetSP xsp1    -==- PutSP m sp2'  = xsp1 m -==- sp2'
GetSP xsp1    -==- GetSP xsp2    = GetSP (\i -> GetSP xsp1 -==- xsp2 i)

Figure 45. Implementation of serial composition with the continuation-based representation.

A definition of the loop combinator loopSP is shown in Figure 46.

loopSP sp = loopSP' empty sp
  where
    loopSP' q NullSP         = NullSP
    loopSP' q (PutSP o sp')  = PutSP o (loopSP' (enter q o) sp')
    loopSP' q (GetSP xsp)    = case qremove q of
                                 Just (i,q')  -> loopSP' q' (xsp i)
                                 Nothing      -> GetSP (loopSP . xsp)

-- Fifo queues
data Queue
empty    :: Queue a
enter    :: Queue a -> a -> Queue a
qremove  :: Queue a -> Maybe (a,Queue a)

Figure 46. Implementation of loopSP with the continuation-based representation.

Example:

Implement runSP :: SP a b -> [a] -> [b].

Solution:

runSP sp xs =
    case sp of
      PutSP y sp'  -> y : runSP sp' xs
      GetSP xsp    -> case xs of
                         x : xs'  -> runSP (xsp x) xs'
                         []       -> []
      NullSP       -> []

20.5 Continuations vs list functions

We have seen two representations of stream processors: one based on list functions and one based on continuations. Which one is better?

Using list functions works well for parallel implementations. Demand is propagated from the output to the input stream by the normal evaluation mechanism of the functional language. Since streams are represented as lists, the standard list functions can be used directly as stream processors.

For sequential implementations, we saw that representing stream processors as functions from streams to streams prevented us from implementing parallel composition. Here, the continuation-based representation seems more attractive, and is the one that we currently employ in the Fudget library. The continuation-based representation also allows stream processors to be detached, moved, and plugged in somewhere else in the program--something that is used in Chapter 25.

Since our implementation is based on a sequential programming language, we do not get true concurrency. As long as all stream processors quickly react to input to avoid blocking other stream processors in the program, this is acceptable in practice. The reactiveness property is not enforced by the compiler, however.

It would be nice to have a representation that works well for both parallel and sequential implementations. Is perhaps the continuation-based representation useful also for parallel implementations? Consider the composition

(sp₁ -*- idSP) -==- sp₂

The first output from the composition should be either the first output from sp₁ or the first output from sp₂, whichever happens to be ready first. But the parallel composition must evaluate to either PutSP ..., or GetSP .... In the first case we have prematurely committed ourselves to taking the output from sp₁ first. In the second case we will not be able to deliver the first output until after sp₂ has delivered its first output. It is not clear to us how the desired behaviour should be achieved.

21 Fudgets as stream processors

Having an implementation of stream processors, we are ready to build fudget combinators and some simple fudgets, based on the stream processor combinators and operations. With Figure 4 in mind, we can view fudgets in two ways:

As plain stream processors which can have I/O effects. This is the abstract view that is presented to the application programmer. With this view, the fudget combinators simply do the same things as the corresponding stream-processor combinators.
As stream processors with explicit high-level and low-level streams. In this chapter, we will take this view in order to implement fudgets.

It should be noted that there are other ways of implementing fudgets. We give two examples suitable for a monadic I/O system in Section 21.5 (references to other work in implementing fudgets are given in Chapter 42).

The fudget implementation used in the library is highly influenced by the synchronised stream I/O system used in version 1.2 of Haskell [HPJWe92].

21.1 Synchronised stream I/O

Synchronised stream I/O can be seen as a variant of the Landin stream I/O in Figure 1, where characters in the output and input streams are replaced by request and response constructors. The program and the I/O system are synchronised, in that for each request that the program produces, one response is produced by the I/O system. Thus, the program and the I/O system can be seen as two parts in a special type of dialogue. The type of a synchronised stream program main is

type Dialogue = [Request] -> [Response]
main :: Dialogue

Each request constructor represents a specific effect, and is defined in the datatype Request in Haskell 1.2:

data Request =  ReadFile String
             |  WriteFile String String
             |  ReachChan Chan
             |  AppendChan Chan String
             ...

The constructor ReadFile f is a request for the I/O system to read the contents of the file with name f. WriteFile f s is a request for writing s to a file with name f. Standard input and output are instances of so called channels: reading the character stream from standard input is requested by ReadChan stdin, and AppendChan stdout s is a request to write s on standard output.

The type of the response that is generated, when a request is carried out, depends on the request constructor. All response types are put in the union type Response:

data Response =  Success
              |  Failure IOError
              |  Str String
              |  IntResp Int
              ...

If the I/O requests are successful, requests for output merely generate a Success response, whereas input requests generate a value tagged with Str,


        IntResp

, or some other constructor depending on its type. If a request fails, an error value tagged Failure is generated.

A program that uses the synchronised stream I/O model can be viewed as an atomic, sequential stream processor, that explicitly uses lists for representing the streams.

21.2 The tagged low-level streams

When adapting the synchronised stream model to Fudgets, we do two modifications. Firstly, we discard the explicit representation of streams as lazy lists, and secondly, we tag the requests and responses, to allow more than one stream processor to do I/O in our program.

We define a fudget of type F hi ho to be a stream processor that can input messages of type hi or tagged responses, and outputs ho messages or tagged requests:

type F hi ho = SP (Message TResponse hi) (Message TRequest ho)

data Message low high = Low low | High high

We could have used the standard type Either, but we prefer using the equivalent type Message for clarity.

The low-level streams carry I/O requests and responses. Fudget combinators like >+< and >==< merge the requests streams from the two argument fudgets. But when a fudget outputs a request we must be able to send the corresponding response back to the same fudget. For this reason, messages in the low-level streams are tagged with pointers indicating which fudget they come from or should be sent to. Since a fudget program can be seen as a tree of fudgets, where the nodes are fudget combinators and the leaves are atomic fudgets, we have chosen to use paths that point to nodes in the tree structure:

type TResponse  = (Path,Response)
type TRequest   = (Path,Request)

type Path = [Turn]
data Turn = L | R     -- left or right

The messages output from atomic fudgets contain an empty path, []. The binary fudget combinators prepend an L or an R onto the path in output messages to indicate whether the message came from the left or the right subfudget. Combinators that combine more than two fudgets (such as listF) uses a binary encoding of subfudget positions. On the input side, the path is inspected to find out to which subfudget the message should be propagated.

As an example, consider the fudget

f = f₁ >==< (f₂ >+< f₃)

When f₂ wants to perform an I/O request r, it puts ([],r) in its low-level output stream. The >+< combinator will prepend an L to the path, since f₂ is the left subfudget. so ([L],r) will appear in the low-level output of

f₂ >+<
        f₃

. Analogously, the >==< combinator will prepend an R, so the low-level output from f will contain ([R,L],r). When a response later appears in the input stream of f, it will be tagged with the same path, [R,L], which will cause the combinators to propagate it to f₂.

As should be apparent, the length of the paths is determined directly by the nesting depth of fudget combinators in the program. For programs that are structured roughly as balanced trees of fudgets, the length of the paths thus grow logarithmically with the number of atomic fudgets in the program. Hence, the overhead of constructing and analysing the paths also grows logarithmically with the number of fudgets. In practice, the maximal path length we have observed varies from 4 for trivial programs (the "Hello, world!" program in Section 9.1), 16 for small programs (the calculator in Section 9.8) and 30 for large programs (the proof assistant Alfa in Chapter 33).

Constructing and analysing the paths of messages is not the only source of overhead in the low-level message passing. Some fudget combinators, most notably the filters (see Chapter 24) treat some commands or events specially. They thus need to inspect all messages that pass through them. When a large number of messages have to be sent, the overhead may become too high. In Section 27.5.3 we present a situation in which we encountered this problem, and give a solution.

An implementation of tagged parallel composition of fudgets is shown in Figure 47. We have reused tagged parallel composition of stream processors by adding the appropriate tag adjusting pre and post processors. The other fudget combinators can be implemented using similar techniques.

>+< :: F i1 o1 -> F i2 o2 -> F (Either i1 i2) (Either o1 o2)
f1 >+< f2 = mapSP post -==- (f1 -+- f2) -==- mapSP pre
  where
    post msg =
      case msg of
        Left (High ho1)         -> High (Left ho1)
        Right (High ho2)        -> High (Right ho2)
        Left (Low (path,req))   -> Low (L:path,req)
        Right (Low (path,req))  -> Low (R:path,req)
    pre msg =
      case msg of
        High (Left hi1)    -> Left (High hi1)
        High (Right hi2)   -> Right (High hi2)
        Low (L:path,resp)  -> Left (Low (path,resp))
        Low (R:path,resp)  -> Right (Low (path,resp))

Figure 47. Tagged parallel composition of fudgets.

When a request reaches the top level of a fudget program, the path should be detached before the request is output to the I/O system and then attached to the response before it is sent back into the fudget hierarchy. This is taken care of in fudlogue. A simple version of fudlogue is shown in Figure 48.

fudlogue :: F a b -> Dialogue
fudlogue mainF = runSP (loopThroughRightSP routeSP (lowSP mainF))

routeSP =
    getLeftSP $ \ (path,request) ->
    putSP (Right request) $
    getRightSP $ \ response ->
    putSP (Left (path,response)) $
    routeSP

lowSP :: SP (Message li hi) (Message lo ho) -> SP li lo 
lowSP fud = filterLowSP -==- fud -==- mapSP Low

filterLowSP = mapFilterSP stripLow

stripLow (Low  low) = Just low
stripLow (High _  ) = Nothing

Figure 48. A simple version of fudlogue for synchronised stream I/O. It does not handle asynchronous input.

This version will suffice for programs where individual fudgets do not block in their I/O requests. If we want to react on input from many sources which comes in an unknown order (e.g. sockets, standard input, the window system, timeout events), this implementation will not be enough, so what should we do? We will discuss this more in Section 22.2. The short answer is that we can detect when the main fudget has become idle (that is, it has evaluated to getSP, and does not wait for a synchronous response). At this point, we perform a system call (namely select) to wait for input to happen on any of our sources of events.

21.3 Writing synchronous atomic fudgets

With the fudget representation in Section 21.2, an atomic fudget which repeatedly accepts a Haskell I/O request, performs it and outputs the response, can be implemented as follows. The combinators getHighSP and


        getLowSP

waits for high- and low-level messages, respectively. They are defined in terms of waitForSP (Section 18.1).

requestF :: F Request Response
requestF = getHighSP $ \ req ->
           putSP (Low ([],req)) $
           getLowSP $ \(_,response) ->
           putSP (High response) $
           requestF

Some requests should be avoided, since when we evaluate their responses, the program might block. For example, we should not use ReadChan stdin, because its response is a lazy list representing the character streams from the standard input.

Files are usually OK to read, a fudget like readFileF (Section 14.2) can be implemented as follows:

readFileF :: F String (Either IOError String)
readFileF = post >^=< requestF >=^< ReadFile
where post (Str s) = Right s
      post (Failure f) = Left f

On its input, it waits for file names to open. The output is either an error value or the content of the file.

21.4 Fudget kernels

The fudget requestF in the previous section provides an interface to the Haskell stream I/O system. To program a fudget with a particular sequential I/O behaviour, a combinator like

-- Preliminary version
streamIoF :: SP (Either Response i) (Either Request o) -> F i o
streamIoF sp = loopThroughRightF (absF sp) requestF

could be used. The argument stream processor sp can talk to requestF using messages tagged Left and to other fudgets through messages tagged Right. However, it seems more appropriate to tag messages with the type


        Message

introduced above, and let the type of streamIoF be

-- Final version
streamIoF :: K i o -> F i o

where

type K i o = SP (Message Response i) (Message Request o)

We call stream processors of type K i o fudget kernels. Fudget kernels are thus used when defining new atomic fudgets with particular I/O behaviours. We define some combinators for describing I/O behaviours in continuation style:

putHighK :: o -> K i o -> K i o
getHighK :: (i -> K i o) -> K i o
nullK :: K i o
doStreamIOK :: Request -> (Response -> K i o) -> K i o

The first three operations correspond directly to the stream-processor combinators putSP, getSP and nullSP, so fudget kernels can be seen as plain stream processors with access to the I/O system.

The implementations of the combinators introduced in this section are shown in Figure 49.

type K i o = SP (Message Response i) (Message Request o)

streamIoF :: K i o -> F i o
streamIoF kernel = mapSP post -==- kernel -==- mapSP pre
  where
    pre   (High i)        = High i
    pre   (Low (_,resp))  = Low resp
    post  (High o)        = High o
    post  (Low req)       = Low ([],req)

putHighK :: o -> K i o -> K i o
putHighK = putSP . High

getHighK :: (i -> K i o) -> K i o
getHighK = waitForSP high
  where
    high (High i) = Just i
    high _ = Nothing

nullK :: K i o
nullK = nullSP

doStreamIOK :: Request -> (Response -> K i o) -> K i o
doStreamIOK request contK =
    putSP (Low request) $
    waitForSP low contK
  where
    low (Low resp) = Just resp
    low _ = Nothing

Figure 49. Fudget kernel combinators.

21.5 Alternative implementations using monadic I/O

Today, Haskell uses the monadic I/O model, which is briefly explained in Section 41.1.3. A monadic version of


        fudlogue

can be defined as follows:

fudIO1 :: F a b -> IO ()
fudIO1 f = case f of
    NullSP                     -> return ()
    GetSP _                    -> return ()
    PutSP (High _) f'          -> fudIO1 f'
    PutSP (Low (path,req)) f'  -> 
           do resp <- doRequest req
              fudIO1 (startupSP [Low (path,resp)] f')

This version still uses the stream I/O constructors internally to represent effects. It relies on an auxiliary function

doRequest :: Request -> IO Response

that converts requests to corresponding monadic effects.

We can also go one step further by throwing out the request and response datatypes, and use the IO monad directly to represent effects. This can be implemented by adding a constructor to the continuation-based stream-processor type:

data  F' i o =  PutF o (F' i o)
             |  GetF (i -> F' i o)
             |  NullF
             |  DoIoF (IO (F' i o))

The constructor DoIoF is used to express I/O effects. This constructor does not have any explicit argument for the continuation fudget, which instead is returned from the I/O computation. To connect fudgets to the I/O system, we use fudIO2:

fudIO2 :: F' i o -> IO ()
fudIO2 f = case f of
             NullF      -> return ()
             GetF _     -> return ()
             PutF _ f'  -> fudIO2 f'
             DoIoF io   -> io >>= fudIO2

We can provide an operation doIoF for plugging in monadic I/O operations in a fudget:

doIoF :: IO a -> (a -> F' i o) -> F' i o
doIoF io c = DoIoF (map c io)

The fudget combinators are defined just as the corresponding for stream processors, with extra cases for the DoIoF constructor. For example, in the case of parallel composition, these are:

DoIoF io  >*< g         = DoIoF (map (>*< g) io)
f         >*< DoIoF io  = DoIoF (map (f >*<) io)

22 Fudget I/O: the gory details

In this chapter, we will dive into some of the gory details in the Fudget library implementation. We will see how the GUI fudgets are designed to fit with X Windows in Section 22.1, using the hierarchical windows that X provides.

Asynchronous I/O is necessary to handle events from many sources such as the X server, standard input, and sockets. The implementation of asynchronous I/O is described in Section 22.2.

The communication between a fudget program and the X server uses the library Xlib [Nye90], which is written in C. Xlib defines a number of data types and calls for creating and maintaining windows, drawing in windows and receiving input events.

There is no standardised foreign-language interface for Haskell, so Haskell programs cannot directly call Xlib. To solve this problem, we have implemented a number of interfaces to Xlib: one of which is compiler independent, and three which are specific for HBC, NHC, and GHC. These interfaces are described in Section 22.3.

22.1 GUI Fudgets

The implementation of GUI fudgets uses the possibility to create hierarchical windows in X Windows, a feature that works as follows.

In X Windows, an application program creates one or more shell windows. We have already seen in Chapter 9 how the fudget shellF is used to create a shell window. These windows appear on the user's desktop and are decorated with a title bar by the window manager. The window manager allows the user to manipulate shell windows in various ways, for example, they might be resized and moved around on the desktop. A shell window thus corresponds to the user's concept of a window.

From the point of view of the application programmer, a shell window provides an area which can be filled with graphics, and which can ``react'' to events such as mouse clicks, which the X server can report to the application as events. The window has its own coordinate system which has its origin in the upper left corner, regardless of the window's position on the desktop. The window system also ensures that when the application draws in a shell window, only areas that are visible are updated. This implies a simplification for the application programmer, since he does not have to consider other applications that the user has started.

So far, this story holds for most window systems. X Windows goes one step further, and allows the programmer to create more windows within the shell window. These can in turn contain even more windows. Each window has its own coordinate system, and can be moved and resized (but not directly by the user of the application, as was the case with shell windows). If a window is moved, all windows inside it will follow, keeping their position in the local coordinate system. In addition, each window is associated with an event mask, which allows the programmer to control how ``sensitive'' the application should be to user input when the pointer is in the window.

The simplification that the concept of shell windows brought us as application programmers can be carried over to hierarchical windows. If each GUI element is put in its own subwindow, the application program does not need to know the element's position in the shell window when drawing in it, for example. It is also possible to have a large subwindow inside a smaller window. By moving the large window, we get the effect of scrolling an area.

Since each GUI fudget has its own window (possibly containing subwindows), we have also used the possibility to associate each GUI fudget with its own event mask, something that we use to limit the network traffic of events from the server to the application. This was initially an important aspect in Fudgets (see Section 22.3.1), and is still an advantage when running programs over low-bandwidth links.

Using one window per GUI fudget also simplifies the routing of events inside the application, which receives one single stream of events from the X server. The handling of events is not centralised, instead the GUI fudgets handle events by themselves. When the X server reports a mouse click, the event contains information about what subwindow was clicked, and the position uses the local coordinate system of the subwindow. The window information is used in fudlogue, which maintains a mapping from window identifiers to GUI fudget paths.

22.1.1 Data types for the X Windows interface

The GUI fudgets uses four datatypes for their communication with the X server via Xlib. First, we have the datatypes


      XRequest

and XResponse (which can be seen as extensions to Request and Response), which allow us to communicate with the X server.

data XRequest
  =  OpenDisplay DisplayName
  |  CreateSimpleWindow Path Rect
  |  CreateRootWindow Rect
  |  CreateGC Drawable GCId GCAttributeList
  |  LoadFont FontName
  |  CreateFontCursor Int
  ...

data XResponse
  =  DisplayOpened Display
  |  WindowCreated Window
  |  GCCreated GCId
  |  FontLoaded FontId
  |  CursorCreated CursorId
  ...

The remaining two datatypes are XCommand, which can be seen as a set of requests without responses, and XEvent, which encode events that the X server asynchronously reports to the application.

data XCommand
  =  CloseDisplay Display
  |  DestroyWindow
  |  MapRaised
  |  LowerWindow
  |  UnmapWindow
  |  Draw Drawable GCId DrawCommand
  |  ClearArea Rect Bool
  |  ClearWindow
  |  CreateMyWindow Rect
  ...

data XEvent
  =  KeyEvent { time::Time, 
                pos,rootPos::Point, 
                state::ModState, 
                type'::Pressed, 
                keycode::KeyCode, 
                keySym::KeySym, 
                keyLookup::KeyLookup }

  |  ButtonEvent { time::Time, 
                   pos,rootPos::Point, 
                   state::ModState, 
                   type'::Pressed, 
                   button::Button}

  |  MotionNotify { time::Time, 
                    pos,rootPos::Point, 
                    state::ModState }

  |  EnterNotify  { time::Time, 
                    pos,rootPos::Point, 
                    detail::Detail, 
                    mode::Mode }

  |  LeaveNotify  { time::Time, 
                    pos,rootPos::Point, 
                    detail::Detail, 
                    mode::Mode }

  |  Expose { rect::Rect, 
              count::Int }
  ...

The datatypes correspond more or less closely to Xlib calls and X events, with one important difference: The Xlib calls and events deal with additional display (a display is a connection to an X server) and window arguments, which are added by fudlogue (see Section 22.2.2).

A number of auxiliary data types that also correspond more or less directly to definitions found in the Xlib library are shown in Figure 50.

-- Resource identifiers
newtype Display = Display Int
-- and similarly for Window, PixmapId, FontId, GCId, CursorId,
-- ColormapId, ...

-- Type synonyms for readability:
type FontName = String
type ColorName = String
type Time = Int
type Depth = Int

-- GC and Window attributes:
data WindowAttributes
  =  CWEventMask [EventMask] 
  |  CWBackingStore BackingStore 
  |  CWSaveUnder Bool
  ...

type GCAttributeList = [GCAttributes Pixel FontId]
data GCAttributes a b = ... -- See Section 27.4.3

-- Various enumeration types:
data EventMask
  =  KeyPressMask | KeyReleaseMask | ButtonPressMask | ButtonReleaseMask
  |  EnterWindowMask | LeaveWindowMask | PointerMotionMask
  |  ExposureMask
  ...

data BackingStore  = NotUseful | WhenMapped | Always

-- Geometry
data Point = Point{xcoord::Int, ycoord::Int}
data Rect = Rect{rectpos::Point, rectsize::Size} -- upper left corner and size
type Size = Point
data Line = Line Point Point -- coordinates of the two end points

Figure 50. Some of the auxiliary types used by the interface to Xlib.

22.1.2 `groupF`: the primitive window creation fudget

GUI fudgets are created with the group fudget:

groupF :: K a b -> F c d -> F (Either a c) (Either b d)

The type of groupF resembles >+<, and indicates that it puts two stream processors in parallel. It will also create a window which will be controlled by the first stream processor, which is a kernel (see Section 21.4). All X commands that the kernel outputs will go to the group fudget's window, and the X events from the window will go to the kernel.

As the name indicates, groupF also groups the GUI fudgets in its second argument, in the following sense. Assume we have the group g:

g = groupF k f

All the windows that are created by groups inside f will be created inside the window created by g, and thus grouped. A consequence is that if the kernel k decides to move its window, all groups inside f will follow.

The atomic GUI fudgets are constructed along the pattern groupF k nullF, that is, they do not have any internal fudgets, just a kernel controlling a window. As an example, consider a group fudget of the form

groupF k₁ (groupF k₂ (groupF k₃ nullF) >+< groupF k₄ nullF)

It will have a window with two subwindows, one of which will have yet another subwindow, as is illustrated in Figure 51.

Figure 51. Four group fudgets. Each group has a kernel stream processor controlling an X window.

A group fudget starts by outputting the command CreateMyWindow r, where r is a rectangle determining the size and position of the window in its parent window. This is a command that does not correspond to any Xlib call. Instead, it will be intercepted by the closest containing group fudget, which will see it as a tagged command of the form (p,CreateMyWindow r). The containing group fudget will convert this to the request CreateSimpleWindow p r. When this request reaches fudlogue, it will be of the form (q,CreateSimpleWindow p r). From this information, fudlogue will be able to deduce in which window the new window should be created, and new window's path is found by concatenating q and p (see also the end of section Section 22.2.2).

The observant reader now asks ``What if there is no containing group fudget?'' The answer is that shellF also counts as a kind of group fudget, and we know that a shellF is always wrapped around GUI fudgets. The main difference between groupF and shellF is that the latter starts by outputting CreateRootWindow instead of CreateMyWindow. The request CreateRootWindow is used to create shell windows.

The group fudget concept can be used for structuring complex fudgets. One example is buttonGroupF:

buttonGroupF :: F (Either BMevents a) b -> F a b
data BMevents = BMNormal | BMInverted | BMClick

It is used in the Fudget library to program push buttons. The enclosed fudget will get messages which indicate what visual feedback is appropriate to give, and when the user actually has clicked in the window. This is an example of a group fudget which is invisible to the user--it only deals with input.

As an example of a group fudget which only deals with output, we can have a look at buttonBorderF,

buttonBorderF :: F a b -> F (Either Bool a) b

which is used to draw the three-dimensional border around push buttons, which can look either pressed or released. The familiar button fudget buttonF is a combination of these two group fudgets and a labelF.

One would think that the buttonBorderF always is used immediately inside a buttonGroupF, but this is not necessary. A good counter example is toggleButtonF, in which a buttonGroupF is wrapped around two fudgets: a buttonBorderF which has a little onOffDispF in it indicating its state, and a


      labelF

. The user can control the toggle button by clicking anywhere in the buttonGroupF, including the label. Note that the group structure in the toggle button coincides with Figure 51.

22.2 Synchronous versus asynchronous I/O

The implementation of stream processors in the Fudget library gives us cooperative multitasking, which implies that stream processors should be programmed in a reactive style. This means that the normal state for a stream processor is to be idle, waiting for input. When such input comes, the stream processor reacts by more or less immediately outputting zero or more messages, and then goes back to the waiting state.

Moreover, fudgets must be cooperative when performing I/O tasks. As we have seen in Chapter 21, the I/O requests from all fudgets in a program are performed in fudlogue. We must make sure that these requests are of a transient nature and can be carried out more or less immediately.

For these reasons, the Fudget library makes a distinction between synchronous and asynchronous I/O. Synchronous I/O, where the whole fudget program must wait for the I/O operation to complete, is only used for transient operations. Its implementation is straightforward, as we saw in Section 21.3. Since synchronous I/O is simple to implement, the Fudget library currently uses it when reading and writing to files, and when writing to sockets, standard output and the X server. (In most cases, but not all, these operations are transient, and a future improvement of Fudgets would be to use asynchronous I/O even for these.) When it comes to reading from standard input or sockets, or waiting for events from the X server, asynchronous I/O is used, since these are operations that are likely to block for arbitrary long periods of time.

22.2.1 Fudgets for asynchronous I/O

The fudgets timerF (Section 14.3) and


     socketTransceiverF

(Section 26.1) are examples of fudgets that must use asynchronous I/O to avoid blocking the whole program. Both of them create descriptors as a first step.

data Descriptor =  SocketDe Socket
                |  TimerDe Timer
                |  DisplayDe Display
                ...

A socket descriptor (of type Socket) is returned as a response to the request OpenSocket h p which opens a socket connection to the port p on host h. Similarly, a request CreateTimer i d results in a timer descriptor associated with interval i and delay d.

Simply creating a descriptor does not result in any asynchronous I/O. A fudget can use the special request

Select :: [Descriptor] -> Request

to signal to fudlogue that it is interested in asynchronous input from a specified set of descriptors.

22.2.2 The asynchronous `fudlogue`

To handle asynchronous I/O, fudlogue maintains a mapping between descriptors and paths to fudgets. We have just seen that fudlogue can receive messages of the form

(p,
     Select ds)

, which announce that there is a fudget with path p which waits for the asynchronous input associated with the descriptors in ds. The function fudlogue collects all descriptors received in this way from all fudgets in the program. When the main fudget evaluates to getSP without an outstanding request, fudlogue knows that it is time to wait for some asynchronous event to happen. It emits a Select request, with all collected descriptors as an argument. The effects of this request are

a call to the UNIX function select, which will wait for input to arrive on any of the descriptors, or a timeout, and
a read operation on the corresponding descriptor (unless it was a timeout).

The response generated is of type AsyncInput:

type AsyncInput = (Descriptor, AEvent)

data AEvent =  SocketAccepted Socket Peer
            |  SocketRead String
            |  TimerAlarm
            |  XEvent (WindowId, XEvent)

As the type AEvent indicates, the response of


     Select

is the descriptor which became ready, paired with the data read.

Using the descriptor table, fudlogue is able to route the received asynchronous input to the waiting fudget.

In addition, fudlogue performs the following translations to handle events to the GUI fudgets:

For each group fudget, fudlogue has an association from its path to the identifier of its window, and a display descriptor (the socket connection to the X server). The group fudgets are unaware of which window or display they are associated with, so fudlogue adds this information to the X related commands and requests from GUI fudgets.
There is also the reversed mapping from window identifiers to paths, which fudlogue uses to route events from the X server to the group fudget associated with the window.

22.3 The interfaces to Xlib

We have already seen in Section 22.1 that we have extended the Request and Response datatypes with constructors divided in XRequest, XResponse,


    XCommand

, and XEvent, that correspond to Xlib calls and X events. (These data types do not provide a complete interface to Xlib. We have implemented those calls that we found useful and extended the interface by need. Also, some parameters have been omitted from some constructors.) Somewhere, the actual I/O that these requests and commands represent must be carried out, and this is done in what we call the interface to Xlib. We have implemented a number of different such interfaces, and they are described in what follows.

22.3.1 A compiler independent interface

The first implementation of Fudgets was done in LML in 1991, and used Landin's stream I/O model (see Chapter 4). A program in LML is a function of type String->String. The first interface to Xlib was done by outputting the calls and receiving the return values and events in text form via the standard output and input channels. The program was connected by a bidirectional pipe to an external C program that performed the actual Xlib calls. The type of the function fudlogue was F i o -> String->String.

The advantage with this method is that it is portable. No changes need to be made to the compiler or its associated run-time system. The same C program can be used with another compiler or even another programming language.

The disadvantage with this method is that it is inefficient because of the parsing and printing of commands, return values and events. By printing them in a simple format, the overhead can be kept down, though. Also, for most user-interface tasks, the throughput need not be very high.

22.3.2 The interface for HBC

To avoid the overhead of the text communication with a separate process, Lennart Augustsson integrated the interface to Xlib with the run-time system of LML. LML uses the synchronised stream I/O (see Section 21.1), so the integration was done by adding new constructors to the request and response types. The extensions are shown in Figure 52. They handle commands and requests corresponding to Xlib calls, requests for socket I/O, and the asynchronous I/O described in Section 22.2.2. The type of the function fudlogue was changed to

F i o
      -> Dialogue

type Dialogue = [Response] -> [Request]

data Request =  ReadFile       String         
             |  WriteFile      String String
             |  ... 
             -- Extensions
             |  XCommand       (XDisplay,XWId,XCommand)
             |  XRequest       (XDisplay,XWId,XRequest)
             |  SocketRequest  SocketRequest
             |  Select         [Descriptor]
             |  ...

data Response =  Success
              |  Str String 
              |  Failure IOError
              |  ...
              -- Extensions
              |  GotSelect AsyncInput
              |  SocketResponse SocketResponse
              |  XResponse XResponse
              |  ...

Figure 52. Extending the Haskell 1.2 dialogue I/O types with requests for the interface to Xlib

The part of HBC's run-time system that handles dialogue I/O is implemented in C. The procedure that implements the Requests was modified to handle the XRequest and XCommand requests by calling a new procedure doxcall outlined in Figure 53. As can be seen in Figure 54, a few lines of C code per supported Xlib call are needed.

PTR doxcall(t, p)
int t; /* tag of the Request */
PTR p; /* pointer to the argument of the Request */
{
  PTR response;

  p = evaluate(p);
  switch(t) {
  case XCommand: /* (Display, Window, XCommand) */
    p = evalArgs(p,3);
    xdocommand((Display *)INTOF(GET1OF3(p)), 
                          INTOF(GET2OF3(p)), 
                          GET3OF3(p));
    response=mkconstr0(RSuccess);
    break;
  case XRequest: /* (Display, Window, XRequest) */
    {
      PTR xresp;
      p = evalArgs(p,3);
      xresp=doxrequest((Display *)INTOF(GET1OF3(p)), 
                                  INTOF(GET2OF3(p)), 
                                  GET3OF3(p));
      response=mkconstr1(XResponse,xresp);
    }
    break;

  default:
    fprintf(stderr, "Unknown X I/O request ...", ...);
    exit(1);
    break;
  }
  return response;
}

void xdocommand(display, wi, p)
...

Figure 53. The C function doxcall was added to HBC's run-time system to handle the extra requests XCommand and XRequest.

PTR
doxrequest(display,wi,p)
     Display *display;
     Window wi;
     PTR p;
{
  PTR rp;
  Window parent;

  switch(getcno(p)) {
  case XRqOpenDisplay: /* DisplayName */
    {
      char displayname[BUFSIZE];
      Display *display;

      evalstring(EARG1(p), displayname, sizeof displayname);
      display=XOpenDisplay(displayname[0] ? NULL : displayname);
      return MkPtrXResp(XRDisplayOpened,display);
    }
    break;
  case XRqCreateRootWindow:     /* Rect */
    ...
  ...
  }

}

Figure 54. The C function doxrequest analyses the XRequest constructor and carries out the corresponding call to Xlib.

22.3.3 The interface for NHC

In the summer 1996, the Fudget library was ported to NHC [Röj95b] for Haskell 1.3 [PH96], to allow fudget programs to take advantage of the new heap profiling features available in NHC [RR96a][RR96b].

The Fudget library could be ported to NHC by a relatively small effort:

A module containing the definitions of the Haskell 1.2 types Request and Response types was added, since none of these are defined in Haskell 1.3.
The fudlogue function was modified to look like fudIO1 in Section 21.5.
The run-time system of NHC was extended to implement the Xlib calls and the other extensions. Fortunately HBC and NHC have very similar run-time systems, so all of the C code written for HBC could be reused with only minor changes, in spite of the differences between the I/O systems. The extensions were made available as a new monadic I/O operation, similar to doRequest in Section 21.5:
```
doXCall :: Request -> IO Response
```
The effect of this function is a call to the procedure doxcall in Figure 53.

22.3.3.1 Support for two-pass heap profiling

Heap profiling can help you improve the memory behaviour of your programs. For example, you may find out using a biographical heap profile that a large portion of the data in the heap is drag, that is, a lot of nodes that are kept in the heap after their last use. You may then use a combination of a biographical profile and a retainer profile to find out which set of functions in the program that are responsible for retaining the drag. This may give you a clue as to how you should change the program to get rid of the drag.

The implementation of certain combined profiles, as described in [RR96b], collects the needed information in two passes, that is, the program is run twice. In order to create two identical runs, the return values of all I/O operations must be recorded during the first run and then played back during the second run.

In order to allow fudget programs to take advantage of the latest heap profiling technology, Niklas Röjemo added the necessary code for recording and playing back the results of the Xlib calls and other extended I/O operations used by the Fudget library. As a typical example, the glue code for the Xlib procedure XOpenDisplay (which we have already seen in Figure 54) was changed as shown in Figure 55.

case XRqOpenDisplay: /* DisplayName */
  {
    char displayname[1000];
    Display *display;

    evalstring(EARG1(p), displayname, sizeof displayname);
    REPLAY_ONE_AND_SKIP(display)
      display=XOpenDisplay(displayname[0] ? NULL : displayname);
    RECORD_ONE(display);
    return MkPtrXResp(XRDisplayOpened,display);
  }
  break;

Figure 55. Changes to the Xlib glue code for two pass heap profiling.

The macros RECORD_ONE and REPLAY_ONE_AND_SKIP expand to code that records the result during the first run and recalls it and skips the actual call during the second run. Their definitions are shown in Figure 56. The variables replay, record and inputFILE are set by NHC's run-time system as appropriate.

#define REPLAY_ONE_AND_SKIP(x) if(replay) { REPLAY(x); } else
#define RECORD_ONE(x) if(record) { RECORD(x); }

#define RECORD(x) fwrite((void *)&(x),sizeof(x),1,inputFILE)
#define REPLAY(x) fread((void *)&(x),sizeof(x),1,inputFILE)

Figure 56. Macros for two pass heap profiling.

22.3.4 The interface for GHC

As a consequence of the NHC implementation, the Fudget library did not depend on a Haskell 1.2 I/O system anymore. This opened the door for an interface to Xlib using the I/O monad and the C-interface in GHC [J{\etalchar{+}}97]. By using this port, it is possible to take advantage of GHC's time profiling tools and possibility to generate efficient code.

The interface to Xlib in GHC is written in a rather ad hoc style using _ccall_ and _casm_ statements. Today, a nicer interface could be created using the foreign-language interface support of Green Card [JNR97].

23 Automatic layout

The layout combinators in Chapter 11 are used to specify the position and size of graphical objects. Today, these objects can be of two types: GUI fudgets or drawings as described in Chapter 27. The original layout system was designed for the GUI fudgets, and its implementation will be described in this section.

The purpose of the automatic layout system is to relieve the application programmer of the task to specify the exact position and size of each GUI fudget. This task has several dynamic aspects. To start with, it depends on factors that are not known until the program has started. For example, the size of a text drawn in a label fudget depends on the the font and size chosen, and can only be determined after the label fudget has communicated with the X server. Individual GUI fudgets can also change their size at any time, and the user might resize a shell window. Both these activities may imply that a number of GUI fudgets must change their position and size.

The layout system also simplifies the implementation of the individual GUI fudget, in that it does not have to worry about the place and position of other GUI fudgets. It must only specify an initial request for a size, and the layout system will allocate a place and actual size.

The implementation of the layout system operates by moving and resizing rectangular units corresponding to the group fudgets (Section 22.1). Remember that a group fudget basically consists of a stream processor controlling an X window, possibly with a number of group fudgets inside it. Each group fudget also contains a piece of the layout system, which is responsible for the placement and sizing of each immediate subgroup fudget. The responsibility is only one level deep: a group fudget does not control any group contained in any of its groups. As an example, the group corresponding to k₁ in Figure 51 is responsible for the layout of k₂ and k₄ (but not k₃).

This division of responsibility is natural, since a group is easily placed and resized by the single Xlib command (ConfigureWindow). All subwindows inside the group will follow and keep their relative positions.

The mechanism of the layout system can be studied by looking at the message traffic between a group fudget and its immediate subgroups.

The group fudget has a filter (other filters are described in Chapter 24), called autoLayoutF, which listens for layout messages that are output on the low-level streams from the subgroups.

data LayoutMessage
  =  LayoutRequest LayoutRequest
  |  LayoutName String
  |  LayoutPlacer Placer
  |  LayoutSpacer Spacer
  ...

The subgroups decide what sizes they need, and output a layout request.

data LayoutRequest
  = Layout {  minsize :: Size,
              fixedh, fixedv :: Bool }

The field minsize is the requested size, and fixedh (fixedv) being true specifies that the size is not stretchable in the horizontal (vertical) direction. (Some placers use this information to allocate extra space to stretchable boxes only.)

The layout filter also receives placers and spacers that the programmer has wrapped around subgroups. Since all layout messages are tagged with a path, the layout filter can associate the placers and spacers with the wrapped subgroups, by analysing the paths. The constructor LayoutName is used in a similar way to associate a subgroup with a name.

The placers and spacers are functions that decide the actual layout. A placer operates on a list of layout requests, yielding one single request for space needed for the placement of all the associated subgroups. Looking back at the discussion of boxes in Section 11.1, we will recognise that there will be one layout request corresponding to each box.

In contrast to the placers, a spacer takes a single request as an argument, and the layout filter maps it on all requests corresponding to the enclosed boxes associated with the spacer, yielding the same number of requests.

type Placer = [LayoutRequest] -> (LayoutRequest, Rect -> [Rect])

type Spacer = LayoutRequest -> (LayoutRequest, Rect -> Rect)

As can be seen from these types, placers and spacers also return a residual function, which we will describe below.

Having collected layout requests and having applied the layout functions to them, the group fudget must decide on one single layout request to output. Since programs should work even if no layout is specified by the programmer, a default placer is wrapped around the subgroups.

The default placer used is called autoP, which picks a suitable layout based on the layout requests at hand. In the current implementation, it simply chooses between verticalP and horizontalP, based on two preferences:

layouts which do not waste space by unwanted stretching are preferred over those that do,
square layouts are preferred over long and narrow layouts.

Future implementations could conceivably take more parameters into account when choosing a layout and have a wider choice of layouts to choose between.

Having produced a single layout request, the group fudget outputs it, and it will be handled by the enclosing group, unless the group is a shell group. In this case, the minsize field in the request is used to set the size of the shell window.

The XEvent type includes constructors that are used to report changes in layout to the GUI fudgets:

data XEvent =  ...
            |  LayoutPlace  Rect
            |  LayoutSize   Size

The propagation of these layout events start in the shell group fudget. When the shell window has been resized, the X server sends a ConfigureNotify event containing the new size to the shell group fudget. Note that this event is generated regardless of whether the resize operation was done by the program (as a result of a layout request) or the user (via the window manager). Anyhow, the shell group fudget generates an event of the form


   LayoutPlace (Rect 0 s)

, to the layout filter. This informs the layout filter that the rectangle from the origin to s is available for the subgroups. Now, the layout filter applies the residual placers and spacers to this rectangle in a reversed pattern. Each residual placer will yield a list of rectangles, where the elements correspond to the list of requests (and thus to the boxes) that was fed to the original placer. Similarly, residual spacers are mapped over rectangles to adjust positions of the associated subgroups.

When this reversed process is finished, the layout filter outputs one LayoutPlace message to each subgroup, which will move itself accordingly, pass the message to its layout filter, and so the process goes on recursively.

When a group receives a LayoutPlace message, it also sends a LayoutSize message to the kernel stream processor, so that it can adjust the graphical content of its window to the new geometry. Note that the kernel only needs to know the size of its window, and not its place. This is due to the fact that all window operations use local coordinates.

23.1 The historic steps of fudget layout

Initially, there was no support at all for layout. The programmer had to explicitly specify the size and position of each GUI fudget.
Then, automatic layout was implemented, with the restriction that each GUI fudget had to correspond to exactly one box. This implied that when two GUI fudgets where composed, a placer had to be specified. The combinators for parallel and serial composition had an extra placer argument. As a result, the layout was too tightly coupled to the dataflow between the GUI fudgets.
The current system allows many boxes per fudget. Together with named layout, this allows more flexible layout.

24 Filter fudgets

The fact that all I/O effects of a fudget are represented through constructors in the datatypes Request,


    Response

and others, opens up the possibility to write what we will call filters, which alter specific aspects of a fudget's input/output behaviour. Filters have type F a b -> F a b, which indicates that they do not tamper with the high-level messages, they only analyse and modify the low-level messages.

A number of problems can be solved by using filters--for example, swapping the meaning of the left and the right mouse buttons, or swapping the black and white colors in GUI fudgets.

In the following sections, we will see two examples of filters from the Fudget library which alter the behaviour of complex fudgets:

The cache filter, which improves the space and time behaviour of fudget programs by letting subfudgets share X server resources (Section 24.1).
The focus filter, which implements click-to-type input style in forms by redirecting keyboard events (Section 24.2).

The filters in the Fudget library are constructed by means of a combinator that resembles loopThroughRightF, and is called loopThroughLowF:

loopThroughLowF :: SP (Either TRequest TResponse)
                      (Either TRequest TResponse) 
                -> F i o -> F i o

Just as loopThroughRightF is often used by application programmers to encapsulate and modify the behaviour of existing fudgets, loopThroughLowF is used in filters located in fudlogue and shellF, and can thus modify certain aspects of all fudgets in an application. The controlling stream processor, which is the first argument to loopThroughLowF, receives as input the stream of all tagged requests that are output from the encapsulated fudgets, and also all tagged responses directed to the same fudgets. It can analyse and manipulate these messages in any manner before outputting them, after which they will continue their way to the I/O system (in the case of the requests), or the fudgets (in the case of the responses). The simplest conceivable filter is

loopThroughLowF idSP

which simply passes through all requests and responses undisturbed, and thus acts as the identity filter.

24.1 The cache filter

Each GUI fudget allocates or queries a number of resources in the X server, such as fonts, font descriptions, graphical contexts and colors. For example, a fudget program with a large GUI may query a large number of font descriptions. This can result in a slow startup time, especially if the round trip delay between the program and server is large. Usually, most GUI fudgets will query the same resources as the others in the program, which seems wasteful. It would be beneficial if the resource allocation could be shared between the GUI fudgets. Not only would this result in a faster startup and less network load, but the program would also consume less memory. This is relevant in the case where font descriptions are queried, since these could occupy a significant amount of the heap.

It is the role of the cache filter to support this resource sharing between fudgets. It is part of fudlogue, which means that all fudgets in the program benefit from the resource sharing.

The effect of the cache filter is most notable on slow connections with high round trip delays, such as dialup connections. To demonstrate this, we have run Cla, one of the demonstration programs from the Fudget distribution, over a dial-up connection using PPP and secure shell (ssh, compression rate 9). The modem speed was 14400 bits per second, and the round trip delay 250 milliseconds on average. To eliminate errors due to different compression rates, the program was started repeatedly, until the startup time converged. Without the cache filter, the minimum startup time for Cla was clocked to 133 seconds. When enabling the cache, the startup time decreased to 9.6 seconds, a speedup factor of over 13. (As a comparison, we also ran Cla on this slow connection without compression: the startup times were 274 seconds with no cache, and 31 seconds with cache. Compression is a good thing!)

The heap usage is also better when the cache is enabled, the peak decreases from 990 to 470 kilobytes.

These figures should not come as a surprise since the GUI in Cla consists of one display, and 28 push buttons which can share the same resources.

Using the cache filter means that there is an overhead in the program. Except for drawing commands, the filter will analyse each request that is output. As a result, the calculator startup time is about 5% longer when the X server runs on the same computer as the calculator. In this case, the connection is fast and has negligible round trip delay.

24.1.1 Implementation

Before describing the implementation, we will show a communication scenario that takes place when a fudget allocates a particular kind of resource, namely a graphics context (GC). First, the fudget outputs the X request

CreateGC 
    d tgc al

, where d is the drawable in which the GC will be used, tgc is a template GC, and al is a list of attributes that the new GC should have. The request is turned into a call to the Xlib function XCreateGC, which returns a reference to a new GC. This is sent back as the response GCCreated gc to the requesting fudget, which brings it to use. When the GC is not needed anymore, the fudget can explicitly deallocate it by outputting the X command

FreeGC
    gc

The idea of using a cache is of course that if a second fudget wants to create a GC with the same template and attributes, we could reuse the first GC, if it is not yet deallocated. So a GC cache maintains table from template and attributes to graphics contexts and reference counts.

It turns out that most resource (de)allocation follows the same pattern as our scenario, if we abstract from the specific request and response constructors. This abstraction is captured in the type RequestType, which expresses whether a request is an allocation, a deallocation, or something else:

data RequestType a r =  Allocate a
                     |  Free r
                     |  Other

The argument to the Allocate constructor carries allocation data that the cache filter uses as search key in the resource table. Similarly, the Free constructor carries the resource that should be freed. In the case of graphics contexts, the allocation data are pairs of template GCs and attribute lists, and the resources are graphics contexts.

The function gcRequestType determines the type of request for graphics contexts:

gcRequestType :: Request -> RequestType (GCId,GCAttributeList) GCId
gcRequestType r = 
  case r of
    CreateGC d tgc al  -> Allocate (tgc,al)
    FreeGC gc          -> Free gc
    _                  -> Other

The general cache filter cacheFilter is parameterised over the function that determines the request type:

cacheFilter :: (Eq a,Eq r) => (Request -> RequestType a r)
                           -> F i o -> F i o

cacheFilter rtf = loopThroughLowF (cache [])
   where cache table = ...

The internal state table is a list of type


    [(a, (r, Int))]

, where the elements are allocation data with associated resources and reference counts.

The definition of a cache for graphics contexts is now simple:

gcCacheFilter :: F i o -> F i o
gcCacheFilter = cacheFilter gcRequestType

The Fudget library defines request type functions like


    gcRequestType

for a number of resources, and the corresponding cache filters, using the general cacheFilter. All these filters are combined into allCacheFilter:

allcacheFilter :: F a b -> F a b
allcacheFilter =
    fontCacheFilter .
    fontStructCacheFilter .
    gcCacheFilter .
    colorCacheFilter .
    bitmapFileCacheFilter .
    fontCursorCacheFilter

This cache filter is wrapped around all fudget programs in


    fudlogue

. One should fear that allcacheFilter would impose a considerable overhead, since all commands must be inspected in turn by each of the six filters. In practice, the overhead is not a big problem.

24.2 The focus filter

When I type on the keyboard, which GUI element should receive the typed characters? Equivalently, which GUI element has the input focus? Initially, the Fudget library implemented the simple model of point-to-type focus, since it is directly supported by X Windows. With point-to-type, a GUI fudget cannot have the input focus unless the pointer is over it. A GUI fudget (such as stringF) signals its interest in focus by configuring its event mask to include KeyPressMask, EnterWindowMask, and LeaveWindowMask. This means that the fudget can receive keyboard input, and also events when the pointer enters or leaves the fudget (crossing events). The crossing events are used to give visual feedback about which fudget has the focus.

A potential problem with point-to-type controlled focus, is that the user must move a hand back and forth a lot between the keyboard and the pointing device (assuming that the pointer cannot be controlled from the keyboard), if she wants to fill in data in a form that consists of several input fields. It is also easy to touch the pointing device accidentally so that the pointer jumps a little, which could result in a focus change.

These problems vanish when using a click-to-type focus model. With click-to-type, the tight coupling between the pointer position and focus is removed. Instead, the user clicks in an input field to indicate that it should have the focus. The focus stays there until the user clicks in another input field. In addition, if the keyboard can be used for circulating focus between the input fields in a form, it can be filled in without using the pointing device.

A limited variant of this improved input model has been added to the Fudget library as a filter in the shell fudgets, leaving the various GUI fudgets unmodified. The limitation is that the model is only click-to-type as long as the pointer is inside the shell fudget. When the pointer leaves the shell fudget, focus goes to whatever application window is under it, unless the window manager uses click-to-type.

24.2.1 Implementation

The implementation of the focus is based on the key observation that GUI fudgets that need keyboard input (let us call them focus fudgets) can be distinguished by the kind of events that they configure their window to report. All focus fudgets are of course interested in key press events, but they also need crossing events, for giving proper visual feedback when they have focus. Therefore, focus fudgets will initially set their window event mask so that ffMask is a subset:

ffMask = [KeyPressMask, EnterWindowMask, LeaveWindowMask]

A simplified implementation of a focus filter is shown in Figure 57.

focusFilter :: F a b -> F a b
focusFilter f = loopThroughLowF (focusSP []) 
                                (simpleGroupF [KeyPressMask] f)

focusSP :: [Path] -> SP (Either TRequest TResponse) 
                        (Either TRequest TResponse)
focusSP fpaths = getSP (either request response)
  where
    request (p,r) =
        case getEventMask r of
          Just mask | ffMask `issubset` mask ->
                putSP (Left (p,setEventMask (mask' r)) $
                focusSP (p:fpaths)
            where mask' = [ButtonPressMask] `union` mask

          _ -> putSP (Left (p,r)) $ 
               focusSP fpaths

    response (p,r) = 
          if keyPressed r 
          then (putSP (Right (head fpaths, r)) $
                focusSP fpaths)
          else if leftButtonPressed 1 r && p `elem` fpaths 
          then putSP (Right (p,r)) $
               focusSP (aft++bef)
          else putSP (Right (p,r))
       where (bef,aft) = break (==path) fpaths

-- Auxiliary functions:
simpleGroupF :: [EventMask] -> F a b -> F a b
getEventMask :: Request -> Maybe [EventMask]
setEventMask :: [EventMask] -> Request -> Request
keyPressed   :: Request -> Bool
leftButtonPressed :: Request -> Bool

Figure 57. A focus filter.

The focus filters reside immediately inside the shell fudgets. To get keyboard events, no matter the position of the pointer (as long as it is inside the shell window), a group fudget is created around the inner fudgets with a suitable event mask. This is done with simpleGroupF, which acts as a groupF without a kernel.

The filtering is done in focusSP, whose argument fpaths accumulates a list of paths to the focus fudgets. This is done by looking for window configuration commands with matching event masks. The event masks of the focus fudgets is modified to mask', so that the windows of focus fudgets will generate mouse button events.

The head of fpaths is considered to own the focus, and incoming key events are redirected to it. If the user clicks in one of the focus fudgets, fpaths is reorganised so that the path of the clicked fudget comes first.

As noted, Figure 57 shows a simplified focus filter. The filter in the Fudget library is more developed; it also handles crossing events, and focus changes using the keyboard. More complex issues, like dynamic creation and destruction of fudgets, are also handled. Still, it ignores some complications, introduced by the migrating fudgets in Chapter 25.

It should also be noted that the X window model supports special focus change events which should rather be used when controlling focus. This fits better with window managers that implement click-to-type.

24.3 Pros and cons of filters

The experience we have had with filters in the Fudget library are both good and bad. On the good side, the filters open the possibility to modify the I/O behaviour of existing software without having to alter its source code. On the other side, although the filters were developed without changing the source code of the GUI fudgets, detailed knowledge about their source code was used in order to decide on what assumptions we could make about their behaviour. For example, we have seen that the focus filter assumes that all GUI fudgets that should be under focus control can be distinguished by analysing their event masks. This complicates the semantics of event masks, something that must be taken into account when programming new GUI fudgets. Similarly, the possible sharing of a resource caused by the cache filter means that imperative operations on resources (such as XChangeGC) must be avoided in the GUI fudgets.

The implementation of filters often involves that a piece of state must be associated with each GUI fudget. This means that the state of some GUI fudgets are spread out in the library, in some sense. One piece resides in the fudget itself as local state, then there is non-local state in the focus filter, and in the fudlogue tables, which are used to route asynchronous events. If fudget state is distributed like this, there is always a danger that it becomes inconsistent, for example when fudgets move or die.

25 Moving stream processors

One distinguished feature of stream processors is that they are not directly connected to their input streams. Rather, a stream processor reacts to one message at a time. A better name would really be message processor, since there are no explicit streams anywhere, only messages. This is in contrast to functions operating on streams as lazy lists, which are instances of the type [i] -> [o] (if we only consider functions from one input stream to one output stream). To get the output stream of such a stream function, one must apply it to the input stream. Once that is done, there is no easy way to detach the stream function from the stream again.

Why would one want to do such a detachment? One reason arises if we want a stream processor to run for a while in one environment, and then move it to some other environment and continue running it there. Remember that stream processors are first class values and may be sent as messages. This, together with the fact that there is no difference (in the type) between a stream processor that has been executing for a while and a ``new'' one, allows us to program a combinator that can catch the ``current continuation'' of an arbitrary stream processor whenever we want.

extractSP :: SP i o -> SP (Either () i) (Either (SP i o) o)
extractSP s = case s of
   PutSP o s  -> PutSP (Right o) $ extractSP s
   NullSP     -> NullSP
   GetSP is   -> GetSP $ \m -> 
                 case m of
                   Right i  -> extractSP (is i)
                   Left ()  -> PutSP (Left s) $ 
                               NullSP

The stream processor extractSP s accepts messages of the form Right i, which are fed to s. Output o from s is output as

Right 
      o

. At any time, we can feed the message Left () to it, and it will output the encapsulated stream processor in its current state as a message, tagged with Left. Note that in general, the stream processor that is output in this way is not equal to the original stream processor s.

So when we demand the continuation, extractSP s outputs it and dies. But why should it die? It might be useful to have it carry on as if nothing had happened. This reminds us of cloning of objects, and forking of processes. The variant is easily programmed, by modifying the last line of extractSP.

cloneSP :: SP i o -> SP (Either () i) (Either (SP i o) o)
cloneSP s = case s of
   PutSP o s  -> PutSP (Right o) $ cloneSP s
   NullSP     -> NullSP
   GetSP is   -> GetSP $ \m -> 
                 case m of
                   Right i  -> cloneSP (is i)
                   Left ()  -> PutSP (Left s) $
                               cloneSP s

Since stream processors are mere values, we do not need any machinery for duplication of state--this is indeed a case where we appreciate purely functional programming.

We can promote these ideas to fudgets as well, although the implementation gets more complicated. In the case of a GUI fudget, some action must be taken to ensure that it brings its associated window along when it moves, for example. We can then program drag and drop for any GUI fudget, as illustrated in Figure 58. In what follows, we will describe a set of combinators for supporting drag-and-drop in fudget programs.

About to drag

While dragging

After dropping
Figure 58. Pictures showing a fudget we are about to drag, while dragging, and after dropping it. After the fudget was dropped, the user changed its text. Note that the output from the moved fudget now goes to Drop area 2.

We call the fudgets that the user can drag and drop drag fudgets, and the areas in which they live drop areas. The communication of drag fudgets between the drop areas is mediated by a single invisible drag-and-drop fudget. A schematic picture of these fudgets is shown in Figure 59.

Figure 59. Schematic view of an invisible drag-and-drop fudget (indicated by the dashed frame) which in this case contains two rectangular drop areas, each of which contains a number of draggable fudgets. The dotted arrow indicates what will happen if a user drags the fudget f₁ from the first to the second area: it will be extracted as a message from the first drop area and reach the drag-and-drop-fudget, which will bounce it to the second drop area.

These three types of fudgets exchange special messages to control the motion of the drag fudgets. To allow the drag fudgets to communicate with the rest of the program independently of these control messages, we pretend for a moment that fudgets have two mid-level input and output connections.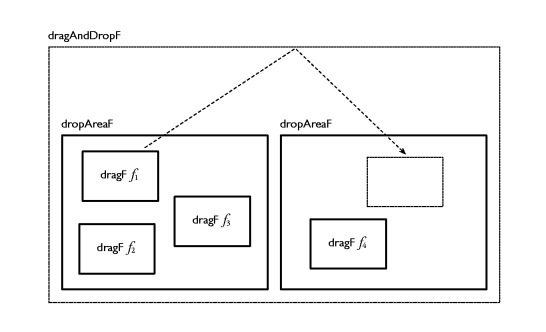

type SF mi mo hi ho = F (Either mi hi) (Either mo ho)

The type SF stands for stratified fudget. With this type, we can think of the message types of stream processors as stratified in three levels. The drag fudgets are formed by the container dragF:

dragF :: F a b -> DragF a b
type DragF a b = SF DragCmd (DragEvt a b) a b

The result type of dragF f is a stratified fudget in which the high-level streams are connected to f, and the mid-level streams are used for control, by means of drag commands and drag events. The drag commands are sent from the drop area to the drag fudgets during drag. The most important drag command is DragExtract, and informs the drag fudget that it has been accepted by another drop area. To this command, the drag fudget responds with an event containing itself:

data DragCmd = 
    DragExtract
 |  ...

data DragEvt a b = 
    DragExtracted (DragF a b)
 |  ...

Since the drag events can contain drag fudgets, we see that it is necessary to parameterise the type DragEvt. The exact type of the drag fudget must be visible in the type of drag events, as well as in other control message types we will introduce in the following. Thus, the type system ensures that a dragged fudget cannot be dropped in an area for fudgets of different type.

The drop area is a stratified variant of dynListF (see Section 13.4):

dropAreaF :: SF (DropCmd a b) (DropEvt a b) (Int,a) (Int,b)

The mid-level messages are called the drop commands and drop events, and are used by the drag-and-drop fudget to control the drop areas. Note that both these types are parameterised, because both can carry drag fudgets as messages. As indicated in Figure 59, the drop area contains drag fudgets, which furthermore are tagged. The high-level messages from these are therefore tagged when they enter or leave the drop area.

There is one drop command that is interesting for the application programmer:

dropNew :: DragF a b -> DropCmd a b

It is used to inject new drag fudgets inside a drop area.

Finally, we have the drag-and-drop fudget, which mediates dropped fudgets between drop areas.

dragAndDropF :: SF (t,DropCmd a b) (t,DropEvt a b) c d -> F c d

The argument to dragAndDropF is a stratified fudget whose mid-level messages should be uniquely tagged drop area messages. The intension is that the stratified fudget contains a list of drop area fudgets. Such a list can conveniently be created using a stratified variant of listF:

listSF :: Eq t => [(t,SF a b c d)] -> SF (t,a) (t,b) (t,c) (t,d)
listSF sfl = pullEither >^=< listF sfl >=^< pushEither

pushEither (Left (t,a))   = (t,Left a)
pushEither (Right (t,a))  = (t,Right a)

pullEither (t,Left a)   = (Left (t,a))
pullEither (t,Right a)  = (Right (t,a))

By means of dragF, dropAreaF, and dragAndDropF, we can program the example (illustrated in Figure 58. As drag fudgets, we use labelled stringInputF's.

drag :: Show i => DragF String String
drag i = dragF $ 
         labAboveF ("Drag me ("++show i++")") $ 
          ((show i++": ")++) >^=< stringInputF

The string output from the drag fudget is prepended with its identity i.

We define a drop area with an associated display which shows the output from the drag fudgets in it. We initialise the drop area by creating a drag fudget in it with the same identity as the drop area.

area :: Show i => 
    i -> SF (DropCmd String String) (DropEvt String String)
            (Int,String) a
area i = vBoxF $ 
           idLeftF (displayF >=^< snd) >==< 
           startupF [Left $ dropNew $ drag i] dropAreaF

Finally, we define a drag-and-drop fudget with two drop areas inside shell fudgets.

dnd :: F (Int,(Int,String)) (Int,a)
dnd = dragAndDropF $ listSF $ 
       [(t,shellF ("Drop area "++show t) (area t)) | t <- [1..2]]

main = fudlogue dnd

25.1 Problems with dragging windows in X Windows

Dragging objects as windows under the pointer in the X Window system is not problem free: it is difficult to determine where the object is dropped when the user releases the mouse button. This release generates a button event which contains information about what window is under the pointer. But this will not be the window in which we drop the object, it will be the object's window itself! If we are content with somewhat less spectacular visual feedback, we could choose not to move the object itself, but change the pointer to a symbol that carries a little object, as is done in Open Windows [Sol97].

What we need is to have the dragged object's window transparent with respect to certain events. We achieve this in a brutal way, by simply zapping a small temporary hole in the object window under the pointer, as shown in the detail.

However, we now have timing problem, which can appear if the user moves the pointer quickly and immediately drops the object. There is a delay in the movement of the pointer and the object, since it is the client which is doing the tracking. With a constant delay, the tracking error is proportional to the speed of the pointer, which means that if the speed is large enough, the pointer will not be above the hole anymore. Currently, we do not know if there exists a good solution to this ``drop problem'' in X Windows.

26 Typed sockets for client/server applications

In this section, we will see how fudgets can be suitable for other kinds of I/O than graphical user interfaces. We will write client/server applications, where a fudget program acts as a server on one computer. The clients are also fudget programs, and they can be run on other computers if desired.

The server is an example of a fudget program which may not have the need for a graphical user interface. However, the server should be capable of handling many clients simultaneously. One way of organising the server is to have a client handler for each connected client. Each client handler communicates with its client via a connection (a socket), but it may also need to interact with other parts of the server. This is a situation where fudgets come in handy. The server will dynamically create fudgets as client handlers for each new client that connects.

We will also see how the type system of Haskell can be used to associate the address (a host name and a port number) of a server with the type of the messages that the server can send and receive. If the client is also written in Haskell, and imports the same specification of the typed address as the server, we know that the client and the server will agree on the types of the messages, or the compiler will catch a type error.

The type of sockets that we consider here are Internet stream sockets. They provide a reliable, two-way connection, similar to Unix pipes, between any two hosts on the Internet. They are used in Unix tools like telnet, ftp, finger, mail, Usenet and also in the World Wide Web.

26.1 Clients

To be able to communicate with a server, a client must know where the server is located. The location is determined by the name of the host (a computer on the network) and a port number. A typical host name is www.cs.chalmers.se. The port number distinguishes different servers running on the same host. Standard services have standard port numbers. For example, WWW servers are usually located on port 80.

The Fudget library uses the following types:

type Host = String
type Port = Int

The fudget

socketTransceiverF :: Host -> Port -> F String String

allows a client to connect to a server and communicate with it.(Footnote: The library also provides combinators that give more control over error handling and the opening and closing of connections.) Chunks of characters appear in the output stream as soon as they are received from the server (compare this with


    stdinF

in Section 14.1).

The simplest possible client we can write is perhaps a telnet client:

telnetF host port = stdoutF >==< 
                    socketTransceiverF host port >==< 
                    stdinF

This simple program does not do the option negotiations required by the standard telnet protocol [RFC854,855], so it does not work well when connected to the standard telnet server (on port 23). However, it can be used to talk to many other standard servers, e.g., mail and news servers.

26.2 Servers

Whereas clients actively connect to a specific server, servers passively wait for clients to connect. When a client connects, a new communication channel is established, but the server typically continues to accept connections from other clients as well.

A simple fudget to create servers is

simpleSocketServerF :: Port -> F (Int,String) (Int,String)

The server allows clients to connect to the argument port on the host where the server is running. A client is assigned a unique number when it connects to the server. The messages to and from simpleSocketServerF are strings tagged with such client numbers. Empty strings in the input and output streams mean that a connection should be closed or has been closed, respectively.

This simple server fudget does not directly support a program structure with one handler fudget per client. A better combinator is shown in the next section.

26.3 Typed sockets

Many Internet protocols use messages that are human readable text. When implementing these, the natural type to use for messages is String. However, when we write both clients and severs in Haskell, we may want to use an appropriate data type for messages sent between clients and server, as we would do if the client and server were fudgets in the same program. In this section we show how to abstract away from the actual representation of messages on the network.

We introduce two abstract types for typed port numbers and typed server addresses. These types will be parameterised on the type of messages that we can transmit and receive on the sockets. First, we have the typed port numbers:

data TPort c s

The client program needs to know the typed address of the server:

data TServerAddress c s

In these types, c and s stand for the type of messages that the client and server transmit, respectively.

To make a typed port, we apply the function tPort on a port number:

tPort :: (Show c, Read c, Show s, Read s) => Port -> TPort c s

The Show and Read contexts in the signature tells us that not all types can be used as message types. Values will be converted into text strings before they are transmitted as a message on the socket. This is clearly not very efficient, but it is a simple way to implement a machine independent protocol.

Given a typed port, we can form a typed server address by specifying a computer as a host name:

tServerAddress :: TPort c s -> Host -> TServerAddress c s

For example, suppose we want to write a server that will run on the host animal, listening on port 8888. The clients transmit integer messages to the server, which in turn sends strings to the clients. This can be specified by

thePort :: TPort Int String
thePort = tPort 8888
theServerAddr = tServerAddress thePort "animal"

A typed server address can be used in the client program to open a socket to the server by means of


    tSocketTransceiverF

tSocketTransceiverF :: (Show c, Read s) => 
       TServerAddress c s -> F c (Maybe s)

Again, the Show and Read contexts appear, since this is where the actual conversion from and to text strings occurs. The fudget tSocketTransceiverF will output an incoming message m from the server as Just m, and if the connection is closed by the other side, it will output Nothing.

In the server, we will wait for connections, and create client handlers when new clients connect. This is accomplished with tSocketServerF:

tSocketServerF :: (Read c, Show s) => 
       TPort c s 
   ->  (F s (Maybe c) -> F a (Maybe b)) 
   ->  F (Int,a) (Int,Maybe b)

So tSocketServerF takes two arguments, the first one is the port number to listen on for new clients. The second argument is the client handler function. Whenever a new client connects, a socket transceiver fudget is created and given to the client handler function, which yields a client handler fudget. The client handler is then spawned inside


    tSocketServerF

. From the outside of tSocketServerF, the different client handlers are distinguished by unique integer tags. When a client handler emits Nothing,


    tSocketServerF

will interpret this as the end of a connection, and kill the handler.

The idea is that the client handler functions should use the transceiver argument for the communication with the client. Complex handlers can be written with a loopThroughRightF around the transceiver, if desired. In many cases though, the supplied socket transceiver is good enough as a client handler directly. A simple socket server can therefore be defined by:

simpleTSocketServerF :: (Read c, Show s) =>
       TPort c s -> F (Int,s) (Int,Maybe c)
simpleTSocketServerF port = tSocketServerF port id

26.4 Avoiding type errors between client and server

By using the following style for developing a client and a server, we can detect when the client and the server disagree on the message types.

First, we define a typed port to be used by both the client and the server. We put this definition in a module of its own. Suppose that the client sends integers to the server, which in turn can send strings:

module MyPort where
  myPort :: TPort Int String
  myPort = tPort 9000

We have picked an arbitrary port number. Now, if the client is as follows:

module Main where -- Client
  import MyPort
  ...
  main = fudlogue (... tSocketTransceiverF myPort ...)

and the server

module Main where -- Server
  import MyPort
  ...
  main = fudlogue (... tSocketServerF myPort ... )

then the compiler can check that we do not try to send messages of the wrong type. Of course, this is not foolproof. There is always the problem of having inconsistent compiled versions of the client and the server, for example. Or one could use different port declarations in the client and the server.

Now, what happens if we forget to put a type signature on myPort? Is it not possible then that we get inconsistent message types, since the client and the server could instantiate myPort to different types? The immediate answer is no, and this is because of a subtle property of Haskell, namely the monomorphism restriction. A consequence of this restriction is that the type of myPort cannot contain any type variables. If we forget the type signature, this would be the case, and the compiler would complain. It is possible to circumvent the restriction by explicitly expressing the context in the type signature, though. If we do this when defining typed ports, we shoot ourselves in the foot:

module MyPort where
  myPort ::  (Read a, Show a) => TPort a String -- Wrong!
  myPort = tPort 9000

We said that this was the immediate answer. The real answer is that if the programmer uses HBC, we might get inconsistent message types, since it is possible to give a compiler flag that turns off the monomorphism restriction, which circumvents our check. This is a feature that we have used a lot (see also Section 40.1).

26.5 Example: a group calendar

Outside the lunch room in our department, there is a whiteboard where the week's activities are registered. We will look at an electronic version of this calendar, where people can get a view like this on their workstation (Figure 60).

Figure 60. The calendar client.

The entries in the calendar can be edited by everyone. When that happens, all calendar clients should be updated immediately.

The calendar consists of a server maintaining a database, and the clients, running on the workstations.

26.5.1 The calendar server

The server's job is to maintain a database with all the entries on the whiteboard, to receive update messages from clients and then update the other connected clients. The server consists of the stream processor databaseSP, and a


      tSocketServerF

, where the output from the stream processor goes to tSocketServerF, and vice versa (Figure 61). The program appears in Figure 62.

Figure 61. The structure of server. The small fudgets are client handlers created inside the socket server.

module Main where -- Server

  import Fudgets
  import MyPort(myPort)

  main = fudlogue (server myPort)

  data HandlerMsg a = NewHandler | HandlerMsg a

  server port = loopF (databaseSP [] [] >^^=< 
                       tSocketServerF port clienthandler)

  clienthandler transceiver = 
     putSP (Just NewHandler) (mapSP (map HandlerMsg))
     >^^=< transceiver

  databaseSP cl db = 
       getSP $ \(i,e) ->
       let clbuti = filter (/= i) cl
       in case e of
             Just handlermsg -> case handlermsg of
                NewHandler -> 
                  -- A new client, send the database to it,
                  -- and add to client list.
                  putsSP [(i,d) | d <- db] $
                  databaseSP (i:cl) db
                HandlerMsg s -> 
                  -- Tell the other clients,
                  putsSP [(i',s) | i' <- clbuti] $
                  -- and update database. 
                  databaseSP cl (replace s db)
             Nothing  -> 
               -- A client disconnected, remove it from 
               -- the client list.
               databaseSP clbuti db

  replace :: (Eq a) => (a,b) -> [(a,b)] -> [(a,b)]
  replace = ...

Figure 62. The calendar server.

The stream processor databaseSP maintains two values: the client list cl, which is a list of the tags of the connected clients, and the simple database db, organised as a list of (key,value) pairs. This database is sent to newly connected clients. When a user changes an entry in her client, it will send that entry to the server, which will update the database and use the client list to broadcast the new entry to all the other connected clients. When a client disconnects, it is removed from the client list. The client handlers (clienthandler) initially announce themselves with NewHandler, then they apply HandlerMsg to incoming messages.The type of the (key,value) pairs in the database is the same as the type of the messages received and sent, and is defined in the module MyPort:

module MyPort where
  import Fudgets
  type SymTPort a = TPort a a
  myPort :: SymTPort ((String,Int),String)
    --          e.g. (("Torsdag",13),"Doktorandkurs:")
  port = tPort 8888

27 Displaying and manipulating graphical objects

So far, we have seen that fudgets can display text, but we have not seen how to create and display other kinds of graphical objects. (You might have wondered how button borders are drawn, for example.) In the first few sections of this chapter we present data types, type classes and fudgets for handling graphics.

Structure editors of various kinds are programs that can make good use of graphics. Examples of such programs are drawing programs, WYSIWYG word processors, file managers, etc. The common characteristic is that they allow you to manipulate a graphical representation of some object on the screen, for example, by selecting a part of the object and performing some editing operation on it (for example, making a word italic in a word processor, or deleting a file in a file manager). The editing operations performed by the user can lead to marginal or radical changes to the structure of the object and its graphical representation. The editor will need to have an efficient mechanism for updating the screen to reflect these changes. The fudget for graphics that we describe in this chapter supports this.

The Fudget library components we have seen so far allow you to build user interfaces that consist of a number of parts that communicate, but we have not seen any mechanisms that allow an arbitrary part to be selected by the user and perhaps replaced by something else, so we have not seen a general mechanism for building structure editors. Some basic fudgets, like toggleButtonF and stringF can be seen as structure editors for particular structures (booleans and strings, respectively). The later sections in this chapter present data types and fudgets that can be used as a starting point when building more general structure editors. In Chapter 28 we go on and describe combinators more directly aimed at building structure editors, or syntax directed editors.

The support for graphics in the Fudget library was prompted by the development of the syntax directed editor Alfa (Chapter 33), and functionality was added to the fudget system as needed for that particular purpose. Some development was also prompted by the work on the web browser described in Chapter 32.

27.1 The class `Graphic`

We have already encountered the class Graphic many times. Many of the GUI fudgets presented in Chapter 9 display graphics. Recall, for example, buttonF:

buttonF :: (Graphic a) => a -> F Click Click

It has an argument that determines what is displayed inside the button. In early versions of the Fudget library, the type of buttonF was

buttonF :: String -> F Click Click

but later, the class Graphic was introduced and many fudgets were generalised from displaying only strings to displaying arbitrary graphical objects. Since the new types are more general than the old ones, the changes are backwards compatible (old programs continue to work unmodified).(Footnote: This kind of change can actually cause ambiguous overloading.)

The Graphic class serves a purpose similar to that of the Show class: types whose values have graphical representations are made instances of the Graphic class, just like types whose values have textual representations are instances of the Show class. As with the Show class, the methods of Graphic class are not often used directly, except when defining new instances, and we discuss them in a later section. The library provides instances in the Graphic class for many standard types.

27.2 Primitive drawing operations

Before we describe the data types that are instances of the Graphic class, we take a look at the low-level interface that allows a fudget to draw something in its window.

The Fudgets GUI toolkit is built on top of the Xlib [Nye90] library level of the X Windows system [SG86] (as described in Section 22.1). This shines through in the Fudget library support for graphics: the primitive drawing operations available in the fudget library correspond directly to what is provided by Xlib.

An interface to the Xlib library calls for drawing geometrical shapes and strings is provided through the data type DrawCommand shown in Figure 63.

data DrawCommand
    =  DrawLine Line
    |  DrawImageString Point String
    |  DrawString Point String
    |  DrawRectangle Rect
    |  FillRectangle Rect
    |  FillPolygon Shape CoordMode [Point]
    |  DrawArc Rect Int Int
    |  FillArc Rect Int Int
    |  CopyArea Drawable Rect Point
    |  CopyPlane Drawable Rect Point Int
    |  DrawPoint Point
    |  CreatePutImage Rect ImageFormat [Pixel]
    |  DrawLines CoordMode [Point]
    ...

Figure 63. The type DrawCommand provides an interface to the Xlib library calls for drawing geometrical shapes and strings.

Apart from the parameters describing the shape to be drawn, the Xlib calls have some additional parameters that are not present in the constructors of the DrawCommand type. As a typical example of the relationship between the Xlib calls and the constructors, consider XDrawLine:

XDrawLine(display, d, gc, x1, y1, x2, y2)
Display *display;
Drawable d;
GC gc;
int x1, y1, x2, y2;

A drawable d (a window or a pixmap) and a graphics context gc are supplied by the fudget that outputs the drawing command. The type XCommand (see Section 22.1.1) contains the following constructor for outputting drawing commands:

data XCommand = ... | Draw Drawable GCId DrawCommand | ...

The display argument can be determined from the drawable. (The current Fudget library supports only one display connection, so nothing extra is needed for this.)

27.3 Types for simple graphical objects

Having seen how a fudget can output drawing commands to draw in its window, we can now take a look at some simple types for graphical objects. These types provide the most low-level interface to the Xlib drawing commands.

27.3.1 `BitmapFile`

Apart from the drawing commands supported through the type DrawCommand, the Fudget library also supports the Xlib library call XReadBitmapFile for reading images (bitmaps) from files:

data XRequest   = ... | ReadBitmapFile FilePath | ...
data XResponse  = ... | BitmapRead BitmapReturn | ...

data BitmapReturn = BitmapBad | BitmapReturn Size (Maybe Point) PixmapId

This means that we can easily create a data type that allows us to use images stored in files as graphical objects.

data BitmapFile = BitmapFile FilePath

instance Graphic BitmapFile where ...

As you can see in Figure 64, by using the type


      BitmapFile

, a program that loads an image from a file and displays it is as just as simple as the "Hello, world!" program (see Section 9.1):

import Fudgets main = fudlogue (shellF "Hello" helloF) helloF = labelF (BitmapFile "hello.xbm")
Figure 64. The graphical version of the "Hello, world" program is just as simple as the textual version in Section 9.1.

27.3.2 `FlexibleDrawing`

The Fudget library provides the following type to create stretchable graphical objects:

data FlexibleDrawing = FlexD Size Bool Bool (Rect -> [DrawCommand])

instance Graphic FlexibleDrawing where ...

The first argument of the FlexD constructor indicates a nominal size, but the actual size is determined by the fudget layout system and depends on the context. The next two arguments indicate the stretchiness, that is, whether the size should be fixed horizontally and vertically, respectively.

The last argument is a function that should produce drawing commands that draw within the given rectangle. The argument is a rectangle rather than just a size to make flexible drawings more efficient to use as parts of structured graphical objects. Although the drawing function could draw completely different things for different rectangle position and sizes, changing the position is expected to have no other effect than a translation, that is,

f (Rect pos size) = moveDrawCommands (f (Rect origin size)) pos

where moveDrawCommands,

moveDrawCommands :: [DrawCommand] -> Point -> [DrawCommand]

moves (translates) drawing commands. Changing the size is expected make the function adjust the drawing to fill the available space, typically by stretching it.

As an example, here are flexible drawings for filled rectangles, horizontal lines and vertical lines:

filledRect, hFiller, vFiller :: Int -> FlexibleDrawing

filledRect = filler False False
hFiller = filler False True
vFiller = filler True False
filler fh fv d = FlexD (Point d d) fh fv (\r->[FillRectangle r])

A sample usage can be seen in Figure 66.

27.3.3 Fixed size drawings

Having defined the type FlexibleDrawing, we can easily define a function for creating graphical objects of a fixed size:

fixedD :: Size -> [DrawCommand] -> FlexibleDrawing
fixedD size dcmds = FlexD size True True drawit
  where drawit (Rect pos _) = moveDrawCommands dcmds pos

The arguments are a list of drawing commands to draw the desired shape and a size. The commands are expected to draw within a rectangle of the indicated size, with the origin as the upper left corner.(Footnote: Instead of leaving it to the user to indicate the size of the drawing, it would be possible to compute a bounding rectangle by inspecting the drawing commands, but doing it accurately in the general case is rather involved and would be less efficient.)

Notice that depending on how you define your FlexibleDrawing value, you may get very different operational behaviour. Using fixedD, you will get a value containing a reference to a list of drawing commands that will be retained in the heap and translated to the appropriate position (by moveDrawCommands) each time the drawing is used. For FlexibleDrawings created like filler above, the drawing commands may be recomputed and thrown away each time the drawing is used. So, although the result on the screen will be the same, how much recomputation that occurs and how much memory is used depends on details in how the program is written and what kind of lambda lifting the compiler does (whether it supports full laziness [Kar92]).

27.4 Types for structured graphical objects

The types for graphical objects presented above lack two important features:

The ability to specify drawing attributes, such as colors, line widths and fonts.
The ability to compose simple objects into larger ones with a layout specified in a simple way.

As discussed in the introduction of this chapter, we also need a way to identify parts of a composite graphical object when building structure editors. We introduce the type Drawing to take care of these needs.

data Drawing label leaf
  =  AtomicD    leaf
  |  LabelD     label   (Drawing label leaf)
  |  AttribD    GCSpec  (Drawing label leaf)
  |  SpacedD    Spacer  (Drawing label leaf)
  |  PlacedD    Placer  (Drawing label leaf)
  |  ComposedD          [Drawing label leaf]

instance Graphic leaf => Graphic (Drawing label leaf) where ...

placedD :: Placer -> [Drawing l a] -> Drawing l a
placedD p ds = PlacedD p (ComposedD ds)

So, composite drawings are trees. The leaves (built with the constructor AtomicD) can contain values of any type, but as seen from the instance declaration above, the drawing can be displayed only if the leaf type is an instance of the Graphic class. The internal nodes can contain:

drawing attributes (the constructor AttribD) that are in effect in the subtree of the node. These are discussed further below.
layout information in the form of spacers and placers (the constructors SpacedD and PlacedD) from the ordinary fudget layout system (Chapter 11).
labels that can be used to identify, or just hold some extra information on, part of a drawing (the constructor LabelD). These have no graphical effect.
Composed drawings (the constructor ComposedD). Most of the time when drawings are composed, it is useful to also specify a layout, so rather than using the constructor ComposedD directly, you use the function placedD.

Since the Drawing type is an instance of the Graphic class, drawings can be displayed by GUI fudgets that create labels, buttons, menus, displays and so on. There is also a fudget that makes use of the properties of the Drawing type:

hyperGraphicsF :: (Eq lbl, Graphic gfx) =>
                  Drawing lbl gfx -> F (lbl, Drawing lbl gfx) lbl

It displays a drawing, with labels in it. When you click on a point in a drawing, the fudget outputs the label of the smallest part containing the point where you clicked. You can replace a part by feeding a pair of a label and a new drawing to the fudget. hyperGraphicsF can thus be the starting point for simple graphical browsers and editors.

27.4.1 Manipulating drawings

Some functions to manipulate parts of drawings are shown in Figure 65. These can be used in the implementation of structure editors. Values of type DPath identify parts of drawings.

type DPath = [Int]

up :: DPath -> DPath

drawingPart :: Drawing a b -> DPath -> Drawing a b
maybeDrawingPart :: Drawing a b -> DPath -> Maybe (Drawing a b)
updatePart :: Drawing a b -> DPath -> (Drawing a b -> Drawing a b) -> Drawing a b
mapLabelDrawing :: (a -> b) -> Drawing a c -> Drawing b c
mapLeafDrawing :: (a -> b) -> Drawing c a -> Drawing c b
drawingLabels :: Drawing a b -> [(DPath, a)]
deletePart :: Drawing a b -> DPath -> Drawing a b
...

Figure 65. Some functions for manipulating parts of drawings.

27.4.2 Mixing graphical objects of different types in one drawing

In a Drawing, all the leaves must have the same type. Although you could draw anything using only leaves of type FlexibleDrawing, it would be more convenient to be able to mix different types of leaves. For this purpose, the Fudget library provides the following type that makes use of existentially quantified types [LO92]:

data Gfx = (Graphic ?a) => G ?a

instance Graphic Gfx where ...  -- trivial

g :: Graphic a => Drawing lbl Gfx
g = AtomicD . G

In the definition of Gfx, ?a is an existentially quantified type variable. The context (Graphics ?a) => limits the domain of the variable to the types in the Graphic class. The result is that the constructor G can be applied to a value of any type in the Graphic class, yielding a value of type Gfx. When you later use pattern matching to extract the argument of G, you will not know what type it has, but you will know that the type is in the Graphic class, so you can apply the methods of that class on it. So, making Gfx an instance of the Graphic class becomes trivial. (The instance declaration is shown in Figure 71).

An example where strings and a FlexibleDrawing are mixed in a Drawing is shown in Figure 66.

placedD verticalP [SpacedD centerS (g "1"), g (hFiller 1), g "x+y"]
Figure 66. A sample drawing with leaves of different types.

The use of existential types gives us a way of packaging data with the methods that operate on it and abstract away from the concrete representation of the data. This is reminiscent of how data abstraction is achieved in object-oriented programming. (The reader is referred to [CW85] for a fuller discussion of the relation between existential types, data abstraction and object-oriented programming.)

27.4.3 Drawing attributes

Most of the Xlib drawing commands have an argument of type GC, a graphics context. This is a data structure containing the values of a number of parameters that affect the result of the drawing commands, but which would be tiresome to have to pass explicitly as arguments every time you draw something. Examples of such parameters, or attributes, are:

foreground and background colors,
which font to use for text,
line width, line style (e.g., solid or dashed), fill style.

Most of these attributes are specified by numbers or elements of enumeration types, but colors and fonts are more troublesome. Colors can be specified using, e.g., color names or RGB values, but before a color can be used in a GC it must be converted to a pixel value. Depending on the visual type of the display, a pixel value can be, e.g., an 8-bit index into a 256 element colormap (for 8-bit PseudoColor displays) or RGB information packed into 16 or 24 bits (for 16-bit and 24-bit TrueColor displays, respectively).

Fonts can be specified by font names, but before they can be used, they have to be converted to font identifiers. Also, if you want to know how much space the text you draw will take up, you need obtain a data structure containing metric information on the font.

The data types provided by the Fudget library for specify drawing attributes are shown below. The types ColorSpec and FontSpec are described further in the next section.

data GCSpec
  =  SoftGC [GCAttributes ColorSpec FontSpec]
  |  HardGC GCtx

data ColorSpec -- see below
data FontSpec -- see below

data GCAttributes color font
  =  GCFunction GCFunction
  |  GCForeground color
  |  GCBackground color
  |  GCLineWidth Width
  |  GCLineStyle GCLineStyle
  |  GCFont font
  |  GCCapStyle GCCapStyle
  |  GCFillStyle GCFillStyle
  |  GCTile PixmapId
  |  GCStipple PixmapId
  ...

data GCtx = GC GCId FontStruct

data FontStruct -- abstract type for font metric info
data GCId -- An Xlib GC
type Width = Int

data GCFunction = GXclear | GXand | GXandReverse | GXcopy | ... | GXset 
data GCLineStyle = LineSolid | LineDoubleDash | LineOnOffDash
data GCCapStyle = CapNotLast | CapButt | CapRound | CapProjecting
data GCFillStyle = FillSolid | FillTiled | FillStippled | FillOpaqueStippled

To include drawing attributes in a Drawing (defined above), you use the constructor AttribD applied to a GCSpec, which usually is the constructor


      SoftGC

applied to a list of attributes containing high-level specifications of fonts and colors. However, before the drawing can be displayed, this high-level specification must be converted into a GC. In addition, to be able to automatically determine the size of text, the metric information for the specified font is required. The high-level drawing attributes are therefore converted into a value of type GCtx by fudgets that display drawings. This conversion may require calls to Xlib library functions like XLoadQueryFont,


      XAllocNamedColor

and XCreateGC. For drawings that are to be displayed many times, making these calls every time can cause a noticeable performance degradation, so the library provides a way to create GCtx values in advance. These can then be included in drawings using GCSpecs with the constructor HardGC. The drawing can then be displayed without making any calls except for the necessary drawing commands. The reason for choosing the names SoftGC and HardGC is that the subdrawings of a node setting the drawing attributes using the SoftGC alternative, inherit the attributes not present in the GCAttributes list from the parent drawing, whereas with the HardGC alternative, all attributes are taken from the given GCtx.

27.4.4 Specifying fonts and colors

To allow fonts and colors to be specified conveniently in different ways, we have introduced the following types and classes:

class ColorGen a where ...
data ColorSpec -- an abstract type
colorSpec :: ColorGen a => a -> ColorSpec

class FontGen a where ...
data FontSpec -- an abstract type
fontSpec :: FontGen a => a -> FontSpec

The following types are instances of the ColorGen class and can be used to specify colors:

type ColorName = String -- color names, as used by Xlib

data RGB = RGB Int Int Int -- RGB values, as used by Xlib

data Pixel -- previously obtained pixel values

Values of the RGB type specifies the intensities of the primary colors red, green and blue, using 16-bit integers. RGB 0 0 0 is black, and

RGB 65535
      65535 65535

is white.

The following types are instances of the FontGen class and can be used to specify fonts:

type FontName = String -- font names as used by Xlib

data FontStruct -- a previously obtained FontStruct

The canonical way of including font and color specifications in a drawing is to do something like this:

blueHelloMsg =
   AttribD (SoftGC [GCForeground (colorSpec "blue"),
                    GCFont (fontSpec "-*-times-*-r-*-18-*")]),
           (g "Hello, world!")

As you can see, this is rather clumsy, so the Fudget library provides the following, more convenient functions:

bgD, fgD ::  ColorGen color =>
             color -> Drawing lbl leaf -> Drawing lbl leaf

fontD ::  FontGen font =>
          font -> Drawing lbl leaf -> Drawing lbl leaf

Using these, you can write the above example like this:

blueHelloMsg = fgD "blue" $ fontD "-*-times-*-r-*-18-*" $
               g "Hello, world!"

27.4.5 Allocating colors and fonts in advance

As mentioned above, you might for efficiency reasons want to allocate colors and fonts in advance, and include the resulting GCtx values in the drawings you construct. For this purpose, the Fudget library provides the following:

wCreateGCtx :: (FontGen b, ColorGen a) =>
               GCtx -> [GCAttributes a b] -> (GCtx -> F c d) -> F c d

rootGCtx :: GCtx

The function wCreateGCtx allows you to create GCtx values, by modifying a template GCtx. You can start from rootGCtx which contains the default settings for all attributes.

27.5 Implementation

How should a fudget that displays Drawings be implemented? Drawings are trees, composed from leaves containing simple graphical objects, using placers and spacers from the ordinary fudget layout system. A natural solution thus seems to be to implement new fudgets for displaying simple graphical objects and then display composed drawings by composing fudgets that display the leaves. While this at first seems like a simple and elegant solution that gives us maximal reuse of existing Fudget library components, remember that we not only want to display drawings: to build structure editors we also need a mechanism that lets the user select and manipulate parts of a structure. We would need to set up a structure where every node in a Drawing is represented by a fudget, and a communication structure which allows us to communicate which each node fudget. Further, in order to be able to replace arbitrary nodes with new drawings, we would have to use the combinator dynF (Section 13.4) at each node.

dynF :: F a b -> F (Either (F a b) a) b

We tried this approach, but when taking all requirements into account, this seemingly natural solution became rather tricky. It also turned out to be rather inefficient and there are several possible reasons for this:

the solution requires a lot of the work to be done by message passing in a complex structure of fudgets. Compared to making function calls, passing messages between fudgets can be expensive (see Section 39.1.2.4).
each graphical fudget is represented by a window in the X Windows system. This means that there will be at least one window per drawing leaf. Creating and maintaining windows requires some work both by the fudget program and the X server.

As a result, we have developed another solution that is now part of the Fudget library. It uses one fudget, graphicsF, to display complete drawings in one window. This has proved to be reasonably efficient. It has allowed us to implement usable, non-trivial applications, the syntax directed editor Alfa (Chapter 33) and the web browser WWWBrowser (Chapter 32) being the largest. A drawback is that some functionality (most notably hit detection and clipping) that in principle could be handled by the window system (and it was in the ``natural'' solution) had to be duplicated in the implementation of graphicsF. The fudget graphicsF could actually be seen as an implementation of a simple window system!

27.5.1 The capabilities of `graphicsF`

Since graphicsF is intended to satisfy all the needs for displaying graphics within the Fudget library, and also be the ground on which applications like syntax directed editors and web browsers can be built, it has been made fairly general. In addition to just displaying graphics, graphicsF

can receive requests to change parts of a complex drawing. This allows you to create editors with efficient screen updates. If graphicsF only accepted complete drawings as input, either the entire window would have to be redrawn after each change, or expensive computations would be needed to calculate the difference between the new and the old drawing.
can highlight part of a drawing in a fairly efficient way. This can be used to implement cursors in editors.
supports receiving mouse and keyboard input. graphicsF indicates which part of a drawing a mouse click occurred in.
can display a background image behind a drawing.
can sound the terminal bell.
can be told to make a certain part of a drawing visible when displaying a large drawing in a scrolling area.

The type of graphicsF is:

graphicsF :: (Graphic a) => F (GfxCommand a) GfxEvent

The definitions of the message types GfxCommand and GfxEvent are show in Figure 67. The constructor


      ChangeGfx

creates messages that allow you to replace or modify the graphical object being displayed. The argument is a list of changes. Each change has the form

(path,(hilite,opt_repl))

where path selects which part of the object should be changed, hilite switches on or off highlighting and opt_repl is an optional replacement for the selected part.

graphicsF is actually a simplification of graphicsGroupF,

graphicsGroupF :: (Graphic gfx) => 
                  (F a b) -> F (Either (GfxCommand gfx) a) 
                               (Either GfxEvent b)

which like groupF, discussed in Section 22.1.2, can contain subfudgets. The fudget activeGraphicsF (discussed in Section 32.3) for displaying drawing with active parts (for example forms in a web browser) is built on top of graphicsGroupF.

There are also customisable versions of these fudgets, allowing you to change parameters like the event mask, border width and resizing policy.

data GfxCommand gfx
  =  ChangeGfx [(DPath,(Bool,Maybe gfx))]
  |  ChangeGfxBg ColorSpec
  |  ChangeGfxBgPixmap PixmapId Bool -- True = free pixmap
  |  ShowGfx DPath (Maybe Alignment,Maybe Alignment)
     -- makes the selected part visible
  |  BellGfx Int -- sound the bell
  |  GetGfxPlaces [DPath] -- ask for rectangles of listed paths

data GfxEvent
  =  GfxButtonEvent { gfxState :: ModState,
                      gfxType :: Pressed,
                      gfxButton:: Button,
                      gfxPaths :: [(DPath,(Point,Rect))] }
  |  GfxMotionEvent { gfxState :: ModState,
                      gfxPaths :: [(DPath,(Point,Rect))] }
  |  GfxKeyEvent    { gfxState::ModState,
                      gfxKeySym::KeySym,
                      gfxKeyLookup::KeyLookup }
  |  GfxPlaces [Rect] -- response to GetGfxPlaces
  |  GfxResized Size

Figure 67. The message types used by graphicsF.

27.5.2 Implementation of `graphicsF`

The fudget graphicsGroupF is implemented using


      groupF

graphicsGroupF subfudgets = groupF graphicsK subfudgets

graphicsK = ...

The behaviour of the fudget is thus implemented in the fudget kernel graphicsK. Here is roughly what graphicsK does in the course of displaying a graphical object.

A graphical object is received on the high-level input.

The sizes of the parts of the graphical object are determined and the required resources (fonts, colors, GCs) are allocated. This part requires calls to Xlib, which are made by


        graphicsK

through the appropriate low-level messages. The result is a value of type MeasuredGraphics (Figure 68), containing leaves of known sizes (i.e., with known LayoutRequests), GCtxs and placers/spacers.

data MeasuredGraphics
  =  LeafM LayoutRequest GCtx (Rect->[DrawCommand])
  |  SpacedM Spacer MeasuredGraphics
  |  PlacedM Placer MeasuredGraphics
  |  ComposedM [MeasuredGraphics]

Figure 68. The type MeasuredGraphics.

The conversion from an arbitrary graphical object to a value of type MeasuredGraphics is done using the methods of the Graphic class. These are shown in Figure 69. Sample instance declarations are shown last in this section.

class Graphic a where
  measureGraphicK :: a -> GCtx -> Cont (K i o) MeasuredGraphics
  measureGraphicListK :: [a] -> GCtx -> Cont (K i o) MeasuredGraphics

  -- Default method for lists:
  measureGraphicListK xs gctx cont = ...
    -- converts xs one element at a time and applies ComposedM
    -- to the resulting list.

Figure 69. The methods of the Graphic class.

The layout is computed, generating a value of type CompiledGraphics (Figure 70), containing bounding rectangles and drawing commands for all the parts. This step is taken by a pure function:

compileMG ::  MeasuredGraphics 
          ->  (CompiledGraphics, LayoutRequest)

data CompiledGraphics = CGraphics Rect Cursor [XCommand] [CompiledGraphics]
  -- The only XCommand used is
  -- Draw MyWindow some_GC some_DrawCommand

type Cursor = Bool

Figure 70. The type CompiledGraphics.

When Expose events are received, the drawing commands of the parts whose bounding rectangles intersect with the damaged rectangles can efficiently be extracted and output. Notice that the drawing commands are kept in the form of XCommands in the CompiledGraphicss. This means that they can be output as they are. No temporary data structures need to be created when responding to an Expose event. This fact, in combination with the use of bounding rectangles allows Expose events to be handled very efficiently. This is noticeable in applications like WWWBrowser and Alfa.
When a part of the drawing is replaced by a new drawing, the new drawing is converted into a MeasuredGraphics and inserted in the old MeasuredGraphics at the appropriate place. (Paths are preserved when a Drawing is converted into a MeasuredGraphics.) A new CompiledGraphics is then computed from the new MeasuredGraphics. Guided by the paths of the changes and the differences between the bounding rectangles of the corresponding parts in the old and new CompiledGraphics, only those parts that have actually changed, or have moved because of the changes, are redrawn.

A shortcoming of current implementation of graphicsF is that it does not handle overlapping parts properly, not because overlapping parts would be too difficult to handle in the current solution, but simply because it has not been important in the applications where graphicsF has been used so far. This means that a drawing with overlapping parts can look different after part of it has been redrawn in response to an


      Expose

event.

Finally, some sample instance declarations for the Graphic class are shown in Figure 71.

instance Graphic Gfx where
  measureGraphicK (G x) = measureGraphicK x

instance Graphic FlexibleDrawing where
  measureGraphicK (FlexD s fh fv drawf) gctx k =
    k (LeafM (plainLayout s fh fv) gctx drawf)
    -- plainLayout is defined in Section 27.6.2.

instance Graphic Char where
  measureGraphicK c = measureString [c]
  measureGraphicListK = measureString

instance Graphic a => Graphic [a] where
  measureGraphicK = measureGraphicListK

instance Graphic Int where        -- and similarly for other basic types
  measureGraphicK i = measureString (show i)

measureString s gctx@(GC gc fs) k =
  let r@(Rect _ size) = string_rect fs s
      d = font_descent fs
      a = font_ascent fs
      p1 = Point 0 a -- left end of base line reference point
      p2 = Point (xcoord size) a -- right end of base line ref point
      drawit (Rect p (Point _ h)) = [DrawString (p+(Point 0 (h-d))) s]
  in k (LeafM (refpLayout size True True [p1,p2]) gctx drawit)
    -- refpLayout is defined in Section 27.6.2.

Figure 71. Some sample instances for the Graphic class.

27.5.3 Efficiency issues in the implementation of `graphicsF`

As mentioned above, when part of a drawing is replaced, graphicsF recomputes the layout of the complete drawing. None of the old layout computations are utilised in this step. This may put an upper limit on how big objects can be handled with reasonable response times in a structure editor. A better solution would be to reuse layout information for parts that are not affected by a change. This is done in the ordinary fudget layout system (see Chapter 23).

Large drawings consist of many DrawCommands. Outputting these one at a time in low-level messages turned out to entail a considerable overhead. For example, redrawing the window after a page scroll in the editor Alfa (Chapter 33) in a typical situation could take 1 second. In an attempt to improve this, we added a new constructor to the XCommand type:

data XCommand = ...  | XDoCommands [XCommands] ...

It allows many commands to be passed in one low-level message, thus allowing all the DrawCommands needed to redraw a window to be passed in one message from graphicsF to the top level of the fudget hierarchy. The message passing overhead thus becomes negligible. Also, caches and other filters (see Chapter 24) that previously had to examine every DrawCommand now only examine one XDoCommands message (they do not look inside). This reduced the above mentioned redrawing time from 1 second to about 0.1 second, which makes a big difference from the user's point of view.

27.6 Extended layout mechanisms

In Chapter 11, we saw placers and spacers suitable for specifying the layout of GUI elements. However, to describe the layout of text in structured graphical objects fully and conveniently, two new features are needed:

Base line alignment. Text has a base line and when text is composed horizontally, the base lines of the pieces should be aligned.
Line wrapping. When displaying longer pieces of text, it is usually not convenient to specify in advance where line breaks should be inserted, since this can depend on the size of the window, which is under user control.

These two new features are provided through two new placers, alignP,

alignP :: Placer

which allows you to compose text with base line alignment, and paragraphP,

paragraphP :: Placer

which does line breaking.

To implement these, two extensions of the layout system were needed. Although they should still be considered to be in an experimental stage, we describe them below.

We also present the idea of conditional placers and spacers, which could be implemented without any extensions. These can be used, for example, to select between different layouts depending on the size of an object.

27.6.1 Reference points

To implement alignP, the layout requests (see Chapter 23) were extended to contain, in addition to the nominal size and the stretchiness, a list of reference points:

data LayoutRequest
  = Layout {  minsize :: Size,
              fixedh, fixedv :: Bool,
              refpoints :: [Point] }

The use of these appear in the Graphic instance for strings (see the function measureString in Figure 71).

alignP places the argument boxes so that the last reference point in one box coincides with the first reference point in the next box. This gives us base line alignment when composing text.

Unlike most other placers, alignP does not stretch the argument boxes. In fact, we have not included a mechanism for specifying how reference points are affected by stretching, so you may get odd layout if a box containing reference points is first stretched by one placer and then aligned with another box containing reference points by alignP.

We have also found use for some spacers that manipulate reference points:

refMiddleS, refEdgesS, noRefsS :: Spacer

moveRefsS :: Point -> Spacer

The spacer refMiddleS replaces the reference points of a box with two reference points placed on the middle of the left and right edges. refEdgesS takes the first and last reference points and moves them horizontally to the left and right edges, respectively. noRefsS removes the reference points from a box. moveRefsS displaces the reference points of a box by a given vector.

The placers and spacers we have presented do not make use of more than two reference points, so it perhaps seems more appropriate to have a pair (instead of a list) of reference points in the layout requests. One can also consider more elaborate use of reference points, for example, different placers might use different sets of reference points. To take a concrete example, when putting equations together horizontally in a comma separated list, you probably want to do base line alignment, but when placing equations in a vertical list, you may want them to appear with the = symbols on the same vertical line. Also, you may want the layout system to choose between horizontal and vertical placement depending on the available space, so the equations must contain reference points for both possibilities, and the placers must be able to choose between them.

27.6.2 Line breaking

The fudget layout system computes the layout in two steps: first a bottom-up pass collects the layout requests from the leaf boxes, giving the required size of the top-level window as a result. Based on this size, the exact placement of each box is computed in a top-down pass. The actual size of each box depends on the requested sizes of all boxes. The actual sizes can also be changed if the user resizes the shell window.

To display text with automatic line breaking, we would like the requested height to depend on the actual width. The line breaking should be redone when the width of the window is changed.

In the original fudget layout system, there was no way for a fudget to ask for a size where the requested height depends on the available width. A fudget could still achieve this behaviour: whenever notified of a size change, it could output a new request with the same width as in the notification but with a new height. Care of course had be taken to avoid generating infinite sequences of notifications and requests and other unpleasant effects. This solution was used in an early version of the web browser described in Chapter 32.

As part of the work on support for structured graphics, we developed a better solution to the line breaking problem. We extended the layout requests with a function that answers the question ``if you can be this wide, how tall do you want to be?''. For symmetry, there is also a function that allows the requested width to depend on the actual height (otherwise flipP would not work). The two functions are called wAdj and hAdj, respectively.

data LayoutRequest
  = Layout {  minsize :: Size,
              fixedh, fixedv :: Bool,
              refpoints :: [Point],
              wAdj, hAdj :: Int -> Size}

The placers now combine such functions in addition to combining nominal sizes and stretchiness. Although the old behaviour can be achieved by using constant wAdj/hAdj functions, the layout requests still contain the usual nominal size. This saves us from having to rewrite all placers and spacers. Also, the usual nominal size is still used rather than the wAdj/


      hAdj

functions on the top level in normal shell windows, while the wAdj function is used in vScrollF (see Section 10.7) , where the width is constrained but the height can vary freely. (Not surprisingly, hAdj is used in


      hScrollF

Changing the data type LayoutRequest meant that all occurrences of the constructor Layout in the Fudget library had to be adjusted. The functions plainLayout and refpLayout were introduced to simplify these adjustments:

plainLayout s fh fv = refpLayout s fh fv []
refpLayout s fh fv rps = Layout s fh fv (const s) (const s) rps

27.6.3 Conditional spacers and placers

Occasionally, we have found use for combinators that try alternative layouts and pick the best one according to some condition. We have implemented an ad hoc choice of such combinators:

ifSizeP  :: (Size->Size->Bool) -> Placer -> Placer -> Placer
ifSizeS  :: (Size->Size->Bool) -> Spacer -> Spacer -> Spacer

stretchCaseS :: ((Bool,Bool)->Spacer) -> Spacer

alignFixedS :: Alignment -> Alignment -> Spacer

The first two allow you to choose between two placers/spacers depending on the size of the resulting box, i.e., if placer₁ and placer₂ yield boxes of size₁ and size₂, respectively, then ifSizeP p placer₁ placer₂ uses placer₁ if p size₁ size₂ is True, and placer₂ otherwise. ifSizeS works analogously for spacers.

stretchCaseS allows you to write spacers that depend on the horizontal and vertical stretchiness of the argument box. alignFixedS is an application of stretchCaseS. It can be used to allow stretchable graphical objects to be stretched while objects of fixed size are aligned. As an example, when buttonF was generalised from displaying strings to arbitrary graphics, we switched from unconditionally centering the label with centerS to conditionally centering it with alignFixedS aCenter aCenter. This means that text labels will be centered as before, while graphical labels may be stretched.

28 Combinators for syntax-oriented manipulation

In Chapter 27, we have seen how graphical objects can be drawn and manipulated using the type Drawing and the fudgets graphicsF and hyperGraphicsF. In this chapter, we will present a set of combinators that can be used for building syntax-oriented editors. Such editors present a graphical view of a structured value in an abstract syntax, for example a program in a programming language. The editors let the user manipulate the (graphical view of) the program in various controlled ways.

One problem the programmer must deal with, when developing syntax-oriented editors, is how the values of the abstract syntax should be represented, and how they should be connected to the graphical objects. We will present a solution where the operations on the abstract syntax is defined closely with the corresponding operations on the graphical objects, to avoid inconsistencies between the abstract syntax and its graphical view.

As a concrete example, consider a grammar for a tiny expression language with arithmetic operations on numbers.

Expr ::= Integer
| Expr Op Expr
Op ::= +
| -
| ×
| /

Such an abstract syntax is straightforward to represent in Haskell using one datatype for each non-terminal in the grammar, and where each alternative corresponds to a data constructor.

data Expr  =  Number Integer
           |  Operation Expr Op Expr
data Op    =  Add 
           |  Subtract 
           |  Multiply 
           |  Divide

How should we connect these datatypes to the graphical objects? One solution is to define Graphic instances for each type, which means that they can be used as leaves in the type


     Drawing

(confer Section 27.4). The drawing can be decorated with labels containing functions for building the abstract syntax when needed, and manipulation functions describing how the user can modify different parts of the abstract syntax. However, all labels in a Drawing must have the same type, which presents a complication when we want to use different datatypes for different non-terminals. In contrast, the combinators in this chapter allow editors of different type, representing different non-terminals, to be combined.

The inspiration of the combinators comes from a certain style of parsing combinators that is part of the functional folklore (the earliest publication we know of is [Röj95a]). If P a is the type of parsers which returns a value of type a, the combinators that are interesting in this context are

ap :: P (a -> b) -> P a -> P b, which combines two parsers sequentially. It also acts as lifted function application, in that the function returned by the first parser is applied to the value returned by the second, yielding a value that the combination returns.
map :: (a -> b) -> P a -> P b, which applies a function to the value that a parser returns.

The ap combinator is left associative (just like function application), and map has higher precedence than

ap

. This allow a concise style when writing parsers. For example, if pExpr is an expression parser, and pOp is an operation parser,

Operation `map` pExpr `ap` pOp `ap` pExpr :: P Expr

parses an expression followed by an operation and another expression, and returns the appropriate Expr value using the Operation constructor.

The next section presents the basic combinators for building editors. Section 28.2 shows how the combinators can be used to build an editor for arithmetic expressions. Section 28.3 discusses how non-local editing operations, like variable renaming, can be handled. The implementation of the combinators is outlined in Section 28.4.

28.1 The `SOM` combinators

The combinators operate on the abstract type

SOM i
       o h a

(Syntax Oriented Manipulation), which represents a value (or piece of abstract syntax) of type a, that can be manipulated through input/output of values of type i and o. The parameter h is used to pass inherited attributes. The parameter a can also be used for passing synthesised attributes, if needed.

A SOM expression not only represents a (structured) value, but also contains information about how different parts of this value might be manipulated, and how the value should be graphically displayed.

somF    ::  h -> SOM i o h a -> F (Either i (SOM i o h a))
                                  (Either o a)

leaf    ::  Graphic g => g -> a -> SOM i o h a
ap      ::  SOM i o h (a -> b) -> SOM i o h a -> SOM i o h b
map     ::  (a -> b) -> SOM i o h a -> SOM i o h b

select  ::  (h -> a -> o) 
        ->  (h -> a -> i -> Maybe (SOM i o h a))
        ->  SOM i o h a
        ->  SOM i o h a

attr    :: (h -> a -> (h',a'))  -> SOM i o h' a
                                -> SOM i o h  a'

Figure 72. The SOM combinators.

The combinators that operate on SOM expressions are shown in Figure 72. The display and manipulation of SOM expressions are controlled by somF. The fudget somF h s will initially display the SOM expression s, given an attribute h to inherit. This expression can at any time be replaced by sending a new SOM expression to the fudget. The fudget can also output the value that the manipulated expression represents. This happens when a new expression is sent to the fudget, or when a selected part of it is replaced. The message types i and o in somF are used for the manipulation of selected subexpressions.

Primitive SOM expressions are built with the function leaf. The arguments to leaf are a graphical object to display, and the value it represents. This combinator is used, together with ap and map, to compose SOM expressions in the same style as parsers.

To manipulate a SOM expression, the user must first select a subexpression. A SOM expression might contain some nodes that are not possible to manipulate (for example, syntactic decorations like keywords), and some that are. The programmer declares that it should be possible to select and manipulate a node by using the select combinator. The composition select f_o f_i s makes the SOM expression s selectable. When the user clicks inside the graphical representation of s, but not inside any inner selectable node, the composition is selected and highlighted. As a result, the output function f_o is applied to the inherited attribute and the current value. The result is output from the fudget somF that contains the composition, and is typically a set of editing operations that are applicable to the selected node. Initially, the current value is merely the value that s represents, but this might change if some part of s is replaced. If some input (typically an editing operation picked by the user) is sent to the fudget while s is selected, the input function f_i is applied to the inherited attribute, the current value and the input, yielding a new expression which replaces select f_o f_i s. The input function also has a choice of returning Nothing, in case the input could not be handled. This is used to delegate input to selectable ancestors, and is covered in Section 28.3.

The combinator attr allows the inherited attribute and the current value to be modified simultaneously. In the composition f `attr` s, f is applied to the inherited attribute and the current value that s represents. The result of f is the attribute that s will inherit, and the current value of the composition.

28.2 Example: manipulating arithmetic expressions

By using leaf, ap and map, we can turn structured values into SOM expressions. As an example, let us consider the expression language from the introduction. We will define the functions edExpr and edOp that turn arithmetic expressions and operators into SOM expressions. Since we do not need any inherited attributes for the moment, and the type of input and output will always be the same, we define a type synonym for the kind of SOM expressions that we will form.

type ArithSOM a = SOM Choice [Choice] () a

edExpr  :: Expr  -> ArithSOM Expr
edOp    :: Op    -> ArithSOM Op

The expression editor edExpr is used in exprF to form the fudget that presents the editor.

exprF :: Expr -> F (Either Choice (ArithSOM Expr))
                   (Either [Choice] Expr)

exprF e = somF () (edExpr e)

When the user selects a subexpression, exprF outputs a list of choices that is presented in a menu. These choices represent the operations that are available on the subexpression. If a choice is picked, it will be sent back to the editor. exprF also outputs the arithmetic expression for evaluation in the main fudget. A screen dump of the program is shown in Figure 73.

Figure 73. An arithmetic expression manipulator. The user has selected the subexpression 2 × 3, which can be replaced by 5, 7, or 0 + 0.

main = fudlogue $ 
  loopF (shellF "Choose" (smallPickListF show >+< 
                         (displayF >=^< (show . evalExpr))) >==<
         shellF "Expression" (scrollF (exprF (Number 0)))
        )

evalExpr :: Expr -> Integer
evalExpr (Number i)       = i
evalExpr (Operation e1 b e2)  = evalOp b (evalExpr e1) 
                                         (evalExpr e2)

evalOp :: Op -> (Integer -> Integer -> Integer)
evalOp Add       = (+)
evalOp Subtract  = (-)
evalOp Multiply  = (*)
evalOp Divide    = \x y -> if y == 0 then 0 else x `div` y

When we define edExpr and edOp, we use a programming style which resembles the one we presented for parsing combinators in the introduction:

edExpr e = selExpr $ case e of

  Number i           ->  Number     `map`  
                         leaf i i  

  Operation e1 b e2  ->  Operation  `map`  
                         edExpr e1  `ap`
                         edOp b     `ap`
                         edExpr e2

Numbers are shown as they are, whereas binary expressions are handled recursively and by means of edOp. Each subexpression can be selected and manipulated by


         selExpr

, which is defined later.

The definition of edOp is similar.

edOp b = selOp $ leaf (showOp b) b

showOp Add       = "+"
showOp Subtract  = "-"
showOp Multiply  = "×"
showOp Divide    = "/"

We define the type Choice to contain expressions that can replace the selected subexpression. Since subexpressions can be of both type Expr and Op, we use a union type for the output.

data Choice =  ReplaceExpr Expr
            |  ReplaceOp Op

When the user selects an expression, we arbitrarily choose to present three alternatives which let the user replace the expression with its value plus or minus one, or replace it with 0 + 0. The interface is not at all the most convenient one could imagine, but it allows a patient user to enter an arbitrary expression (the + can be replaced with any of the other operators, as we will see below). This part of the editor could of course be elaborated as desired.

selExpr :: ArithSOM Expr -> ArithSOM Expr
selExpr = select outf inf
  where 
    outf _ e = map ReplaceExpr
                   [Number (evalExpr e-1),
                    Number (evalExpr e+1),
                    Operation (Number 0) Add (Number 0)]
    inf _ _ = map edExpr . stripExpr

stripExpr (ReplaceExpr e)  = Just e
stripExpr _                = Nothing

If the user picks one of the choices, it will be propagated to the selected node, the expression is extracted from the type union, and a replacement SOM expression is formed. However, the type system cannot prevent programming errors that result in an operator being sent to


         selExpr

. To get a more robust program, the function


         stripExpr

ignores the input in this case and returns


         Nothing

When an operator is selected, we present a choice of the four arithmetic operators.

selOp :: ArithSOM Op -> ArithSOM Op
selOp = select outf inf
  where
    outf _ _ = map ReplaceOp [Add,Subtract,Multiply,Divide]
    inf  _ _ = map edOp . stripOp

stripOp (ReplaceOp b)  = Just b
stripOp _              = Nothing

28.3 Non-local manipulation

With the combinators presented so far, we can define local manipulation operations. The user can select a SOM subexpression, and arbitrary replacements can be specified for that expression. If a manipulation would imply a change in other parts of the expression, we are forced to replace the complete expression globally, by sending a new SOM expression to somF. There are situations where we want the possibility to specify replacements that are somewhere in between the local and global alternatives. Suppose that we want to add variables to our arithmetic expressions. We would then like to provide an operation for changing the name of a variable, by selecting one occurrence (possibly the binding occurrence), and give a new name to it. This is an operation that affects the whole subtree that starts with the binding of the variable.

This effect can be achieved by using the possibility to delegate input as follows. Recall that the input function (the second parameter of select) can return Nothing for input that cannot be handled. Instead of discarding the input, somF will delegate it to the closest selectable ancestor, and apply its input function. This delegation propagates towards the root of the SOM expression, until a select node is found that accepts the input.

In the case of variable manipulation, delegation can be used to propagate input to the node where the variable is bound. We will do this in the following section, where we present a variant of the expression manipulator in Section 28.2, extended with variables.

28.3.1 Extended example: manipulating variables

We extend the datatype Expr with constructors for variables and let expressions.

data Expr =
    ...
  | Var Name
  | Let Name Expr Expr

type Name = String

In the construction of a SOM expression, we assume the presence of an environment where we can lookup the value of variables.

type Env = [(Name,Integer)]

We will use the inherited attribute for propagating the environment. The type of SOM expressions we will use are instances of ArithEnvSOM.

type ArithEnvSOM a = SOM Choice [Choice] Env a

We introduce the additional combinators drLeft or drRight to prepend or append a graphical decoration to an expression.

drLeft   :: Graphic g => g -> SOM i o h a  -> SOM i o h a
drRight  :: Graphic g => SOM i o h a -> g  -> SOM i o h a

These are used for drawing keywords, as we will see in the case of let expressions.

The associativity of ap, drLeft and drRight are set so that we avoid parentheses, at least in this application.

infixl 3 `ap`
infixr 8 `drLeft`
infixl 8 `drRight`

Haskell does not declare any fixity for map, which means that it gets a default declaration.

infixl 9 `map`

But the type of map suggests that it should be right associative. If it were, and had the same precedence level as drLeft, we could skip the parentheses in expressions like

f `map` (d `drLeft`
           s)

. If local fixity declarations were allowed in Haskell, we could fix the fixity.

edExpr e = 
  let infixr 8 `map`
  in  ...

Local fixity declarations are not allowed in Haskell, so we give map a new name with the desired fixity.

infixr 8 `mapp`

mapp :: (a -> b) -> SOM i o h a -> SOM i o h b
mapp = map

With mapp, we can construct SOM expressions in the style shown in in Figure 74.

edExpr :: Expr -> ArithEnvSOM Expr
edExpr e = case e of

  Number i           -> selExpr   $  Number                      `mapp` 
                                     leaf i i                    
                                                               
  Operation e1 b e2  -> selExpr   $  Operation                   `mapp`
                                     edExpr e1                   `ap`
                                     edOp b                      `ap`
                                     edExpr e2                    
                                                               
  Var n              -> selVar n  $  Var                         `mapp`
                                     leaf n n                    
                                                               
  Let n e1 e2        -> selLet    $  extendEnv                   `attr`
                                     Let                         `mapp`
                                     "let"                       `drLeft`
                                     edName n                    `ap` 
                                     "="                         `drLeft`
                                     (dropEnv `attr` edExpr e1)  `ap`
                                     "in"                        `drLeft`
                                     edExpr e2

extendEnv  ::  Env -> Expr -> (Env,Expr)
extendEnv  =   \env e@(Let n e1 _) -> ((n,evalExpr env e1):env,e)

dropEnv    ::  Env -> Expr -> (Env,Expr)
dropEnv    =   \env e -> (tail env,e)

Figure 74. The function edExpr extended for variables.

The function extendEnv will be applied to the current let expression, from which it will extract sufficient information to extend the environment that the body should inherit. To avoid that the right-hand side in the let expression also inherits the extended environment, we use the function dropEnv to pop the added binding. (If we want to allow recursive declarations, we omit dropEnv.)

Note that we have also used different selection functions for different kinds of expressions. Variables are handled by selVar, let expressions by selLet, and the others by selExpr.

The binding occurrence of a variable is handled by edName (Figure 75), and selecting such a name results in a choice of renaming it. For simplicity, we pick an arbitrary new name that is not present in the environment by using freshVar.

edName :: Name -> ArithEnvSOM Name
edName n = selName $ leaf n n

selName ::  ArithEnvSOM Name -> ArithEnvSOM Name
selName = select outf inf
  where outf env n = [renameCommand n env]
        inf _ _ _ = Nothing

renameCommand :: Name -> Env -> Choice
renameCommand old env = Rename old (freshVar env)

freshVar :: Env -> Name
freshVar env = head (map (:[]) ['a'..] \\ map fst env)

Figure 75. The editor for variable names.

The input function in selName ignores all input, which instead is delegated to selLet.

We have extended the manipulation type with a command for renaming a variable.

data Choice =
  ...
  | Rename Name Name

The selection functions are defined in Figure 76.

selExpr :: ArithEnvSOM Expr -> ArithEnvSOM Expr
selExpr = selExpr' (const []) exprInf

selLet :: ArithEnvSOM Expr -> ArithEnvSOM Expr
selLet = selExpr' (const []) letinf
  where letinf env (Let n e1 e2) (Rename n' new) | n == n'
                   = Just (edExpr (Let new (rename n new e1) 
                                           (rename n new e2)))
        letinf env e i = exprInf env e i


selVar :: Name -> ArithEnvSOM Expr -> ArithEnvSOM Expr
selVar n = selExpr' (\env -> [renameCommand n env]) exprInf

selExpr' :: (Env -> [Choice])
         -> (Env -> Expr -> Choice 
                         -> Maybe (ArithEnvSOM Expr))
         -> ArithEnvSOM Expr
         -> ArithEnvSOM Expr
selExpr' xchoices inf = select outf inf
  where outf env e = xchoices env ++ 
                     map ReplaceExpr
                           ([ Number (v+1)
                            , Number (v-1)
                            , Operation n0 Add n0
                            , Let (freshVar env) n0 n0 ]
                           ++ map (Var . fst) env
                           )
           where v   = evalExpr env e
                 n0  = Number 0

exprInf :: Env -> Expr -> Choice -> Maybe (ArithEnvSOM Expr)
exprInf env _ = map edExpr . stripExpr

Figure 76. The selection functions for expressions.

The functions for let expressions and variables are variants of the original selExpr from Section 28.2. We define a parameterised version (selExpr'), which lets us add choices and specify the input function. Note that we have added choices for all variables in scope.

The standard selection function (selExpr) does not have any additional choices, whereas the selection function for let expressions (selLet) defines an extended input function which handles the renaming command. For a renaming command to match, the old variable must equal the bound variable. Otherwise, input is meant for some outer let expression. We assume a function rename, where rename old new e substitutes new for old in e.

When selecting a variable, we extend the expression selection menu with a renaming choice. Variable renaming can then take place at any occurrence of a variable. Note that we do not handle renaming in the input function, it is the same as in selExpr.

The rest of the program is almost the same as in the first example, except that we pass the empty environment as an initial inherited attribute in exprF. The program is seen in action in Figure 77.

exprF :: Expr -> F (Either Choice (ArithEnvSOM Expr))
                   (Either [Choice] Expr)
exprF e = somF emptyEnv (edExpr e)

emptyEnv :: Env
emptyEnv = []

Figure 77. Manipulating variables. There are additional choices for the variables in the environment. Since a variable is selected, there is also a choice of renaming it.

28.4 The implementation of the `SOM` combinators

We have taken the approach to implement SOM as a datatype with constructors corresponding to the combinators leaf, select, map and ap. Since the types of the arguments to map and ap have variables that do not show up in the result type, we use the possibility to specify local existential quantification using variables beginning with ? in the datatype declaration. Again, existential quantification in datatypes proves to be a useful extension to Haskell (see also Section 27.4.2).

data SOM i o h a =  
    Select (h -> a -> o) 
           (h -> a -> i -> Maybe (SOM i o h a))
           (SOM i o h a)
   |  Map (?b -> a) (SOM i o h ?b)
   |  Ap (SOM i o h (?b -> a)) (SOM i o h ?b)
   |  Attr (h -> ?a -> (?h,a)) (SOM i o ?h ?a)
   |  Leaf Dr a
   |  Decor (Dr -> Dr) (SOM i o h a)

The first four constructors correspond directly to the respective combinators.

select  = Select
ap      = Ap
attr    = Attr
instance Functor (SOM i o h) where map = Map

The first argument to the Leaf constructor is a drawing:

type Dr = Drawing SOMPointer Gfx

The label type SOMPointer, which is defined later, is used to identify what part of a SOM expression the user has selected. The type Gfx is used to store arbitrary graphical objects in the leaves (Section 27.4.2). In the definition of leaf, we turn these graphics into drawings by means of g (which was defined in Section 27.4.2).

leaf    ::  Graphic g => g -> a -> SOM i o h a
leaf d a = Leaf (g d) a

The final constructor in SOM is Decor, and can be used to define layout or add additional graphics on a part of a SOM expression. Its first argument is a function which will be applied to a drawing that is constructed from its second argument. The combinators drLeft and drRight uses this constructor:

drLeft d n   = Decor (\d' -> hboxD [g d,d']) n
drRight n d  = Decor (\d' -> hboxD [d',g d]) n

The fudget somF is built around a


         hyperGraphicsF

, which outputs a SelectionPtr whenever the user selects a subexpression.

data Dir = Le | Ri
type SelectionPtr = [Dir]

A SelectionPtr is a list of turns to take whenever an Ap node is encountered in the SOM tree, and points out a select node. Using the function


         somOutput

in Figure 78, somF can get the output choices of a selected node.

somOutput :: h -> SOM i o h a -> SelectionPtr -> o
somOutput h n p = case n of
   Select outf _ n  -> case p of 
                         []  -> outf h (somValue h n)
                         _   -> somOutput h n p
   Ap f n           -> case p of
                         Le:p  -> somOutput h f p
                         Ri:p  -> somOutput h n p
   Map _ n          -> somOutput h n p
   Attr f n         -> somOutput (fst (apAttr f h n)) n p
   Decor _ n        -> somOutput h n p

Figure 78. The function somOutput.

If somF receives an input choice for the selected node, the function somInput (Figure 79) is applied to the input and the selection pointer, to get the modified SOM tree.

somInput :: h -> SOM i o h a -> i -> SelectionPtr 
         -> Maybe (SelectionPtr,SOM i o h a)
somInput h n i p = case n of
   Select o inf n  -> case p of 
                        []  -> myInput
                        _   -> mapSOM (Select o inf) 
                                      (somInput h n i p) 
                               ++ myInput
                       where myInput = map (\n->([],n)) 
                                           (inf h (somValue h n) i)
   Ap f n          -> case p of
                        []    -> Nothing
                        Le:p  -> map (mapPair ((Le:),(`ap` n))) 
                                     (somInput h f i p)
                        Ri:p  -> map (mapPair ((Ri:),(f `ap`)))
                                     (somInput h n i p)
   Map f n         -> mapSOM (Map f) 
                             (somInput h n i p)
   Attr f n        -> mapSOM (Attr f) 
                             (somInput (fst (apAttr f h n)) n i p)
   Leaf dr a       -> Nothing
   Decor f n       -> mapSOM (Decor f) 
                             (somInput h n i p)
 where mapSOM = map . apSnd
       mapPair f g (x,y) = (f x,g y)

Figure 79. The function somInput.

somInput also returns the pointer to the node whose input function accepted the input, which is used by somF to update the correct part of the drawing. If all input functions ignore the input, somInput returns Nothing.

The functions somOutput and somInput use the function somValue, to get the current value of a SOM expression, and the function apAttr, to apply attribute functions (Figure 80).

somValue :: h -> SOM i o h a -> a
somValue h n = case n of
   Select _ _ n  -> somValue h n
   Ap n1 n2      -> (somValue h n1) (somValue h n2)
   Map f n       -> f (somValue h n)
   Leaf _ a      -> a
   Attr f n      -> snd (apAttr f h n)
   Decor _ n     -> somValue h n

apAttr ::  (h -> a -> (h',a')) 
       ->  h 
       ->  SOM i o h' a 
       ->  (h',a')
apAttr f h n = h'a' where h'a' = f h (somValue (fst h'a') n)

Figure 80. The functions somValue and apAttr.

The recursive definition in apAttr mirrors the fact that attributes and values can have cyclic dependencies.

The implementation of somF is shown in Figure 81, and as mentioned previously, it is built around hyperGraphicsF. The auxiliary functions tohg, out, updateDr, and replaceDr are routing functions that are typical when programming with loopThroughRightF. The function out is used when outputting messages from somF, and updateDr and replaceDr are used when updating part of or the whole of the drawing in the hyperGraphicsF. (Compare with the type of hyperGraphicsF in Section 27.4.)

The controlling stream processor ctrl has an internal state which consists of the SOM expression being edited (n), and a pointer to the selected node (p). If there is no selected node, p is Nothing. An incoming message to ctrl is either a click from the hyperGraphicsF, indicating a new selection by the user (handled by click), an input choice (handled by input) or a new SOM expression (handled by replace).

In click, the old selection cursor is removed, and a new node is selected.

In input, it is checked that there is a selection, and that a replacement node can be obtained from somInput. In this case, the appropriate subdrawing is replaced, and selected.

somF    ::  h -> SOM i o h a -> F (Either i (SOM i o h a))
                                  (Either o a)
somF h n = loopThroughRightF 
              (absF (ctrl n Nothing))
              (hyperGraphicsF (unselectedSomDr n))
  where
    tohg  = putSP . Left
    out   = putSP . Right
    updateDr   = tohg . Left . unselectedSomDr
    replaceDr  = tohg . Right

    unselectedSomDr = somDrawing []

    ctrl n p = getSP $ click `either` (input `either` replace)
      where
       same = ctrl n p

       click p' = maybe id (deselect n) p $ 
                  selectO n p' $ 
                  ctrl n (Just p')

       input i = flip (maybe same) p $ \jp -> 
                 flip (maybe same) (somInput h n i jp) $ \(rp,n') ->
                 replaceDr (rp,somDrawing rp n') $
                 selectO n' jp $
                 out (Right (somValue h n')) $
                 ctrl n' p

       replace n' = updateDr n' $
                    ctrl n' Nothing

       -- Select subnode and send its output.
       selectO n p = select n p . out (Left (somOutput h n p))
       
       -- Draw cursor
       select = setselect cursor

       -- Remove cursor
       deselect = setselect id 
       setselect cu n p = replaceDr (p,cu (somDrawing p n))

       -- The cursor is a frame around the node
       cursor d = placedD overlayP (boxD [d,(g (frame' 1))])

-- Extract selected subdrawing
somDrawing :: SelectionPtr -> SOM i o h a -> Dr

Figure 81. The function somF.

29 Type directed GUI generation

29.1 Introduction

In the HCI (Human Computer Interaction) school [Shn98], it is good design to first concentrate on a good user interface when developing a GUI application, then implement the functionality behind. For example, the Logical User-Centered Interactive Design Methodology (LUCID) [Kre96] consists of six stages, in which the third stage includes the development of a so-called key-screen prototype using a rapid prototyping tool. After a stage of iterative refinement, this prototype is turned into a full system in the fifth stage.

To promote quick development of prototype programs, a programmer might prefer to concentrate on the functionality, and ignore the GUI design (at least to start with). Since this method can make life easier for the programmer, and to put it in contrast with HCI, we call it PCI (Programmer Computer Interaction) oriented.

With the PCI method, the GUI must be generated automatically somehow. The basic idea is simple, and can be seen as the GUI variant of the Read and Show classes in Haskell, which allow values of any type to be converted to and from strings, using the functions read and show:

read  :: Read a => String -> a
show  :: Show a => a -> String

Part of the convenience with these classes is that instances can be derived automatically by the compiler for newly defined datatypes. By using read and show, it is easy to store data on files, or exchange it over a network (as is done in Chapter 26).

In this section, we will define the class FormElement, which plays a similar role to Read and Show, but for GUIs. Form elements are combined into forms, which can be regarded as simple graphical editors that allow a fixed number of values to be edited. They are often used in dialog windows to modify various parameters in a GUI application.

Assuming that all the necessary instances of FormElement are available, we show how forms can be generated automatically, entirely based on the type of the value that the form should present.

29.2 The `FormElement` class

An individual form element displays a value of some type a. Whenever this value is changed, it will be output by the element. Such a change occurs when a user enters a new value, but it should also be possible to change the value from the program itself.

A candidate type for form elements for a type a is a fudget with the type a both on input and output.

type FormF t = F t t

The form element class has a method which specifies such a fudget.

class FormElement t where
  form      :: FormF t
  formList  :: FormF [t]

instance (FormElement t) => FormElement [t] 
  where form = formList

We have used the standard trick of adding a special method formList which handles lists, so that we can get an instance for strings (this is discussed in Section 40.2).

We can now define instances for the basic types integers, booleans, and strings.

instance FormElement Int
  where form = intInputF

instance FormElement Bool 
  where form = toggleButtonF " "

instance FormElement Char 
  where formList = stringInputF

We also need instances for structured types. The fundamental structured types are product and sum.

instance (FormElement t, 
          FormElement u) => 
          FormElement (Either t u) 
  where form = vBoxF (form >+< form)

instance (FormElement t, 
          FormElement u) => 
          FormElement (t,u) 
  where form = hBoxF (form >·< form)

Note the vertical layout of alternatives, whereas elements within an alternative have a horizontal layout.

The combinator >·< puts two fudgets in parallel, just like >+< and >*<, but input and output are pairs.

(>·<) :: F a1 b1 -> F a2 b2 -> F (a1, a2) (b1, b2)
f >·< g = pairSP >^^=< (f >+< g) >=^^< splitSP

pairSP :: SP (Either a b) (a,b)
pairSP = merge Nothing Nothing where 
   merge ma mb = 
     (case (ma,mb) of
        (Just a,Just b) -> put (a,b)
        _ -> id) $ 
     get $ \y -> case y of
          Left a   -> merge (Just a) mb
          Right b  -> merge ma (Just b)

Input to f >·< g is split, the first component is fed into f, and the second component is fed into g. The combined fudget will not output anything until both f and g has output something. After this has occurred, a message from one of the subfudgets f or g is paired with the last message from the other subfudget and emitted.

We are ready for a small example. The figure shows a form which can handle input which either is an integer, or a pair of a string and a boolean.

myForm :: FormF (Either Int (String,Bool))
myForm = border (labLeftOfF "Form" form)

An extended example connects the input and output of the form with fudgets to demonstrate the message traffic:

main = fudlogue $ 
         shellF "Form" $
                  labLeftOfF "Output" (displayF >=^< show)
            >==<  myForm
            >==<  labLeftOfF "Input" (read >^=< stringInputF)

This program is illustrated in Figure 82.

Figure 82. First, the user has entered the string "Hello" and activated the toggle button. Then, the user entered a number in the integer form element. The last picture is a simulation of how the form can be controlled by the program, in this case by entering a value in the Input field. The value sets the form and is propagated to the output.

29.3 Some suggestions for improvements

The little form program is a tangible example of how types can influence the semantics of a Haskell program through overloading. To some extent, this style allows a programmer to freely modify the type of data structures during development without the need to change the code that deals with the GUI. Together with the automatic layout system, this provides (limited) automatic GUI generation. However, as can be seen in Figure 82, there is much room for improvement of the form. For example, there is no visual feedback that reveals the state of a form element of type Either. It would be desirable to highlight the part that is valid (or to dim the other part).

This generation can also be performed for user defined datatypes by using polytypic programming [JJ97], based on the instances for products and sums. Polytypic programming allows us to define how instances should be derived, based on the structure of the user-defined datatype. For more complicated (for example recursive) types, it might be a better idea to base the form elements on the fudgets for structured graphics in Chapter 27.

After the functionality is there, the programmer's attention might turn to the look of the forms, and we need a way to tune them. An approach that immediately comes to mind is to add an extra attribute parameter to the form method.

class FormElement a t where
    form :: a -> FormF t

If we have an instance FormElement a t, we can construct a form for a type t, given an attribute value of type a. A problem with this approach is that currently, only one parameter may be specified in a class declaration in Haskell. Multi-parameter classes are allowed in Mark Jones' Gofer [Jon91], which also allows instance declarations for compound types like String. With these features, we could define instances as follows.

instance (FormElement a t,
          FormElement b u) => FormElement (a,b) (Either t u)

  where form (a,b) = vBoxF (form a >+< form b)

instance (FormElement a t,
          FormElement b u) => FormElement (a,b) (t,u)
  where form (a,b) = hBoxF (form a >·< form b)

instance Graphic a => FormElement a String
  where form a = labLeftOfF a $ stripInputSP >^^=< stringF

instance Graphic a => FormElement a Int
  where form a = labLeftOfF a $ stripInputSP >^^=< intF

instance Graphic a => FormElement a Bool
  where form a = toggleButtonF a

30 Parameters for customisation

There are many aspects of GUI fudgets that one might want to modify, e.g. the font or the foreground or background colours for displayF. The simple GUI fudgets have some hopefully reasonable default values for these aspects, but sooner or later, we will want to change them.

In early versions of the Fudget library, the GUI fudgets had several extra parameters to make them general and adaptable to different needs. For example, the type of displayF was something like:

displayF :: FontName -> ColorName -> ColorName -> F String a

Having to specify all these extra parameters all the time made it hard to write even the simplest program: when creating a program from scratch, it was next to impossible to write even a single line of code without consulting the manual. When we wrote programs on overhead slides or on the blackboard, we always left out the extra parameters, to make the code more readable.

A simple way to improve on this situation would be to introduce two versions of each GUI fudget: one standard version, without the extra parameters, and one customisable version, with a lot of extra parameters:

displayF :: F String a
displayF' :: FontName -> ColorName -> ColorName -> F String a

displayF = displayF' defaultFont defaultBgColor defaultFgColor

This would make it easy to use the standard version, and the blackboard examples would be valid programs. But the customisable version (displayF') would still be hard to use: even if you just wanted to change one parameter, you would have to specify all of them and you would have to remember the order of the parameters. So, we went a step further.

First, we wanted be able to change one parameter without having to explicitly give values for all the other ones. A simple way of doing this would be to have a data type with constructors for each parameter that has a default value. In the case of displayF, it might be

data DisplayFParams =  Font FontName 
                    |  ForegroundColor ColorName
                    |  BackgroundColor ColorName

Then, one could have the display fudget take a list of display parameters as a first argument:

displayF' :: [DisplayFParams] -> F String a

We no longer have to remember the order of the parameter, and, whenever we are happy with the default values, we just leave out that parameter from the list, and all is fine.

displayF = displayF' []

However, suppose we want to do the same trick with the button fudget. We want to be able to customise font and colours for foreground and background, like the display fudget, and in addition we want to specify a ``hot-key'' that could be used instead of clicking the button:

data ButtonFParams =  Font FontName 
                   |  ForegroundColor ColorName
                   |  BackgroundColor ColorName
                   |  HotKey (ModState,Key)

Now, we are in trouble if we want to customise a button and a display in the same module, because in a given scope in Haskell, no two constructor names should be equal. Of course, we could qualify the names with module names, but this is tedious. We could also have different constructor names to start with (ButtonFFont, ButtonFForegroundColor etc.), which is just as tedious.

30.1 A mechanism for default values

Our current solution(Footnote: The basics of this design are due to John Hughes.) is not to use constructors directly, but to use overloaded functions instead. We will define a class for each kind of default parameter. Then, each customisable fudget will have instances for all parameters that it accepts. This entails some more work when defining customisable fudgets, but the fudgets become easier to use, which we feel more than justifies the extra work.

Let us return to the display fudget example, and show how to make it customisable. First, we define classes for the customisable parameters:

type Customiser a = a -> a

class HasFont a where
   setFont :: FontName -> Customiser a

class HasForegroundColor a where
   setForegroundColor :: ColorName -> Customiser a

class HasBackgroundColor a where
   setBackgroundColor :: ColorName -> Customiser a

Then, we define a new type for the parameter list of


      displayF

newtype DisplayF = Pars [DisplayFParams]

and add the instance declarations

instance HasFont DisplayF where
   setFont p (Pars ps) = Pars (Font p:ps)

instance HasForegroundColor DisplayF where
   setForegroundColor p (Pars ps) = Pars (ForegroundColor p:ps)

instance HasBackgroundColor DisplayF where
   setBackgroundColor p (Pars ps) = Pars (BackgroundColor p:ps)

The type of displayF will be

displayF :: Customiser DisplayF -> F String a

We put these declarations inside the module defining


      displayF

, making DisplayF abstract. When we later use displayF, the only thing we need to know about


      DisplayF

is its instances, which tell us that we can set font and colours. For example:

myDisplayF = displayF (setFont "fixed" .
                       setBackgroundColor "green")

If we want to have buttonF customisable in the same way, we define the additional class:

class HasKeyEquiv a  where
   setKeyEquiv :: (ModState,Key) -> Customiser a

The button module defines

newtype ButtonF = Pars [ButtonFParams]

and makes it abstract, as well as defining instances for font, colours and hot-keys. Note that the instance declarations for font and colours will look exactly the same as for the display parameters! (We can reuse the constructor name Pars as long as we define only one customisable fudget in each module.) In the Fudget library implementation, we have used cpp macros to simplify the implementation of customisable fudgets and avoid code duplication.

We can now customise both the display fudget and the button fudget, if we want:

myFudget = displayF setMyFont >+< buttonF (setMyFont.setMyKey) "Quit"
   where setMyFont  = setFont "fixed"
         setMyKey   = setKeyEquiv ([Meta],"q")

If we do not want to change any default values, we use standard, which does not modify anything:

standard :: Customiser a
standard p = p

standardDisplayF = displayF standard

30.2 Naming conventions for the customisable GUI fudgets

The GUI fudget library is designed so that when you start writing a fudget program, there should be as few distracting parameters as possible. Default values will be chosen for colour, fonts, layout, etc. But a customisable fudget must inevitably have an additional argument, even if it is standard. We use short and natural names for the standard versions of GUI fudgets, without customisation argument. So we have


buttonF :: String -> F Click Click
buttonF = buttonF' standard

buttonF' :: Customiser ButtonF -> String -> F Click Click
buttonF' = ...

displayF :: F String a
displayF = displayF' standard

displayF' :: Customiser DisplayF -> F String a
displayF' = ...

and so on. This way, a programmer can start using the toolkit without having to worry about the customisation concept. Later, when the need for customisation arises, just add an apostrophe and the parameter. One could also have the reverse convention and use apostrophes on the standard versions, something that sounds attractive since apostrophes usually stand for omitted things (in this case the customiser). But then a programmer must learn which fudgets are customisable (and thus need an apostrophe), even if she is not interested in customisation.

30.3 Dynamic customisation

Apart from specifying parameters in the program text, most parameters can in fact be changed dynamically, if needed. Therefore, each customisable fudget comes in a third variant, which is the most expressive. Their names end with two apostrophes. These dynamically customisable fudgets allow customisers as input messages in addition to the usual message type:

type CF p a b = F (Either (Customiser p) a) b

As an example, the button and the display fudgets can be dynamically customised:

buttonF'' :: Customiser ButtonF->String->CF ButtonF Click Click
displayF'' :: Customiser DisplayF -> CF DisplayF String a

30.4 Discussion

Collecting all parameters in a customiser rather than using a high arity function has a number of advantages:

When you use a customisable fudget, you only need to mention the parameters you want to change from the default value.
Future versions of the library can add new parameters without invalidating old code.
You do not have to remember the order of the parameters.
By using Haskell's class system for overloading, the name of the customiser for a certain parameter can be the same for all fudgets that have that parameter. For example, all fudgets that display text can be customised with the setFont function.
Customisers are first class values. They can be named and used in many function calls, even in calls to different functions. (Section 30.1 contains an example of this.)

The last point is an advantage even when compared to what you can do in languages with support for default values for parameters.

In the X Windows system, customisation is done via a resource database, where the application can lookup values of various parameters. The database is untyped, that is, all values are strings, so no static type checking can be performed. With our customiser solution, parameters are type checked. In addition, the compiler can check that the parameters you specify are supported by the fudget in question, whereas parameters stored in the resource database are silently ignored if the are not supported.

Disadvantages with this method, as compared to such languages, are that

defining customisable functions is more cumbersome,
you do not get an error message if you specify the same parameter twice, and that
you need two versions of each customisable function (for example, buttonF and buttonF')

We used lists of parameters in the implementation of customisers:

newtype DisplayF = Pars [DisplayFParams]
data DisplayFParams = ...

An alternative would be to use record types instead:

data DisplayF = Pars { font::FontName,
                       foregroundColor, backgroundColor :: ColorName }

instance HasFont DisplayF where setFont f p = p { font=f }
...

This would make it easier to extract the values of the various parameters in the implementation of the customisable fudgets. A possible disadvantage with this representation is that in the implementation of dynamically customisable fudgets, it would be more difficult to tell what parameters have actually been changed. With the list representation, only the parameters that have been changed occur in the list.

31 Gadgets in Fudgets

Gadgets [Nob95] is a GUI toolkit on top of a modified version of the Gofer interpreter [Jon91]. As will be described the related work (Section 41.3.1), the term Gadgets stands for Generalised Fudgets, and [Nob95] indeed presents fudget combinators in Gadgets. In this section, we describe a purely functional implementation of the underlying process scheduler in Gadgets, which enabled us to port the source code for Gadgets to Haskell and use it on top of Fudgets.

The Gofer implementation of the process scheduler is implemented in C as part of Gofer's runtime system. A feature of the scheduler is that it attempts to keep the message queues short by giving higher priority to processes that read from channels with many waiting messages.

A limitation in the Gofer implementation of Gadgets resulted in that for each channel, at most one process can be waiting for arriving messages, and channels must be explicitly claimed by a process before trying to read from them.

The functional scheduler that we will describe is not as advanced as the original one, but it is simpler and does not have the above mentioned limitation. Before describing the functional scheduler, we give an overview of the process primitives as they appear in the original Gofer version.

31.1 Wires and processes in Gadget Gofer

Gadget Gofer relies on an extension of Gofer with processes and wires. The type Process s represents processes which have an internal state of type s. Communication between processes is asynchronous, and mediated by typed wires.

type Wire a = (In a,Out a)
data In a = In Int
data Out a = Out Int

The communication along wires is directed, one end is input only (In a), the other is output only (


      Out a

). If a process only knows the input (output) end of a wire, it can only read from (write to) it. Note that the wire ends are merely represented by integer identifiers, although the types carry extra information about the message type.

Wires are created by the primitive primWire.

primWire :: (Wire a -> Process s) -> Process s

(Just as with stream processors, the sequential behaviour of a process is programmed in a continuation passing style). To transmit something along a wire, one uses primTx.

primTx :: Out o -> o -> Process s -> Process s

A process can wait for input from many wires simultaneously, by using guarded processes. A guarded process (which we denote AGuarded s) is a process continuation that is waiting for input from one wire, and is formed by


      primFrom

primFrom :: In m -> (m -> Process s) -> AGuarded s

Given a list of guarded processes, we can wait for input to any of them by primRx.

type Guarded s = [AGuarded s]
primRx :: Guarded s -> Process s

Now, why are there two primitives for receiving input, when there is only one for transmitting output? The reason is that although we could combine primFrom and primRx,

-- not general enough!
primRxFrom :: [(In m, (m -> Process s))] -> Process s -> Process s
primRxFrom = primRx . map (uncurry primFrom)

the combination forces us to wait for messages of the same type. The introduction of guarded processes hides the message types and allows a process to select input from wires of different type.

Processes need not live forever, they can die by calling primTerminate.

primTerminate :: Process s

Last but not least, a process can spawn a new process.

primSpawn :: Process s' -> s' -> Process s -> Process s

Thus, primSpawn p s₀ c will spawn the new process p, giving it initial state s₀, and continue with c.

Gadget Gofer also uses primitives for claiming and disowning wires, and requires that a wire should be claimed by a process before attempting to receive from it. Since the functional scheduler does not have this restriction, we ignore them in the following. The presentation will also ignore

that primRx actually takes an additional debugging argument, and
the existence of the global, polymorphic wire ends nci and nco, which are not connected to anything.

31.1.1 Connecting processes to the world

Wires are not only used for inter-process communication, they also interface the processes to the outside world. There are three primitive device processes that, when spawned, attach wires to the keyboard, the mouse, and the screen.

keyboard  :: In KeyboardCmnd  -> Out KeyboardEvnt  -> Process s
mouse     :: In MouseCmnd     -> Out MouseEvnt     -> Process s
screen    :: In [ScreenCmnd]  -> Out ScreenEvnt    -> Process s

The mouse and keyboard can be configured by transmitting mouse or keyboard commands, respectively, whereas the screen commands are used for drawing. The events report key presses, mouse clicks, mouse movements, and exposure events.

These three primitives are started once inside the Gadget window system. For example, the keyboard process is started with

wire $ \smk ->
wire $ \ksm ->
spawn (keyboard (ip smk) (op ksm))

After this, the keyboard events are read from op smk, and the keyboard is configured by writing to ip ksm.

To execute a process with a given initial state, Gadget Gofer provides the primitive primLaunch.

primLaunch :: Process s -> s -> IO ()

31.1.2 Manipulating the process state

A process uses the operations readState and


        setState

readState :: (s -> Process s) -> Process s
setState :: s -> Process s -> Process s

In Gadget Gofer, the type Process s is a synonym for a function from s to s, that is, a state transformer.

type Process s = s -> s

The implementation of readState and showState is then straightforward.

readState   c = \s  -> c s s
setState s  c = \_  -> c s

31.2 A functional process implementation

The Fudgets implementation of Gadgets is purely functional, written in Haskell, which means that all primitives described above are defined within Haskell. The ``runtime'' system (the process scheduler) is also written in Haskell, except that it uses a type cast (not defined in ordinary Haskell) at one place, as we will see.

In the functional version, processes cannot have the simple function type s -> s any more, since we must be explicit about the effects that processes can have. Instead, we will define the process type in steps, where we start with a stream-processor type that handles messages related to the keyboard, mouse and screen. On top of the stream-processor type, we define a state monad (SPms) with operations for manipulating a state in addition to the I/O operations of the stream processor. The state is used by the scheduler, and is used to define a simple process type Process0, which amounts to the Gadget processes except that they do not have any local state. Having done this, we define the full Gadget processes on top. The steps are summarised in the following table.

Process Gadget processes with state
Process0 Processes without state
SPms Stream-processor state monads
SP Plain stream processors

31.2.1 The stream-processor monad with state

We can build a stream-processor monad with state by using the type SPms:

type SPms i o s a = (a -> (s -> SP i o)) -> (s -> SP i o)

A computation of type

SPms i o s
        a

can input messages of type i, output messages of type o, manipulate a state of type s, and return a value of type a through the following operations:

getSPms    :: SPms i o s i
putSPms    :: o -> SPms i o s ()
loadSPms   :: SPms i o s s
storeSPms  :: s -> SPms i o s ()

getSPms      = \k s  -> getSP $ \i -> k i s
putSPms o    = \k s  -> putSP o $ k () s
loadSPms     = \k s  -> k s s
storeSPms s  = \k _  -> k () s

31.2.2 Processes without state

We use the state stream-processor monad to implement the stateless processes, called Process0. The state of the stream processor is used by the scheduler for bookkeeping.

type Process0 i o =  SPms i o (SchedulerState i o) ()

data SchedulerState i o = SS{  freeWire   :: Wno
                            ,  messageQs  :: MessageQueues
                            ,  ready      :: [Process0 i o]
                            ,  guarded    :: [Guarded0 i o]
                            ,  input      :: [i -> Process0 i o]
                            }

Just as in the Gofer implementation, we use integers to identify wire ends, except that we call the integers wire numbers (Wno).

newtype Wno    = Wno Int
newtype In a   = In Wno
newtype Out a  = Out Wno

What follows are definitions of the primitives for creating wires and processes, and communication over wires. We suffix the primitives with a 0 to indicate that they operate on processes without local state.

A new wire is allocated with primWire0, which increments the field freeWire in the state, and hands a fresh wire to the continuation.

primWire0 :: (Wire a -> Process0 i o) -> Process0 i o
primWire0 c = 
  do ps@(SS{ freeWire = w@(Wno i) }) <- loadSPms
     storeSPms ps{ freeWire = Wno (i+1) }
     c (In w, Out w)

The second component in the scheduler state (messageQs) is a mapping from wire numbers to queues of not yet delivered messages.

type MessageQueues = IntMap (Queue Msg)

The types IntMap and Queue implement integer maps and Okasaki's queues [Oka95] come from HBC's library, and have the following signatures:

module Queue where
  empty  :: Queue a   
  snoc   :: a -> Queue a -> Queue a   
  tail   :: Queue a -> Queue a   
  head   :: Queue a -> a   
  null   :: Queue a -> Bool

module IntMap where
  empty   :: IntMap a
  modify  :: (a -> a) -> a -> Int -> IntMap a -> IntMap a
  delete  :: Int -> IntMap a -> IntMap a   
  lookup  :: Int -> IntMap a -> Maybe a

The operations are standard, except modify, which deserves an explanation. The expression

modify f
        a i m

applies the function f to the entry i in m if it exists. Otherwise, it inserts the value a at i.

Each message is paired with the wire number. Since different wires can have different type, messages can also be of different type. We use an existential type (an extension to Haskell provided by HBC) to hide the message type when putting messages in the queue.

data Msg = Msg ?a

Constructing values of type Msg is easy, but when de-constructing them, we cannot assume anything about the type of the argument. We return to this problem later.

Sending a value on a wire amounts to queueing the wire number together with the value.

primTx0 ::  Out a -> a -> Process0 i o -> Process0 i o
primTx0 (Out wno) msg p = 
   if wno == ncWno then p 
   else
     do ps@(SS{ messageQs, ready }) <- loadSPms 
        storeSPms ps{ messageQs = addMsg wno (Msg msg) messageQs
                    , ready = p:ready}
        scheduler

addMsg :: Wno -> Msg -> MessageQueues -> MessageQueues
addMsg wno m = modify (snoc m) (snoc m Queue.empty) wno

The field ready holds a list of processes that are ready to run. When spawning off a new process, we put it on the ready list.

primSpawn0 :: Process0 i o -> Process0 i o -> Process0 i o
primSpawn0 p' p = 
   do ps@(SS{ ready }) <- loadSPms
      storeSPms ps{ ready = p':ready }
      p

There is also a list of processes waiting for messages, stored in the field guarded. The elements are lists of stateless guarded processes (AGuarded0 i o).

data AGuarded0 i o = AGuarded0 Wno (?a -> Process0 i o)

A guarded process is a wire number and a function which takes a message as a parameter. The actual type of the message is hidden in AGuarded0, so that we can form a list of guarded processes regardless of what message type they are waiting for.

type Guarded0 i o = [AGuarded0 i o]

A guarded stateless process is formed with primFrom0.

primFrom0 :: In m -> (m -> Process0 i o) -> AGuarded0 i o
primFrom0 (In wno) f = AGuarded0 wno f

The function primRx0 will wait for a message to arrive to any of the guarded processes in the first parameter. It adds the guarded processes to the state, and then jump to the scheduler to find another process to execute.

primRx0 :: Guarded0 i o -> Process0 i o -> Process0 i o
primRx0 g def = 
  do ps@(SS{ guarded }) <- loadSPms
     storeSPms ps{ guarded = g:guarded }
     scheduler

The scheduler's (Figure 83) job is to apply guarded processes to matching messages, move them to the ready list, and pick one from the ready list to run. In case the ready list is empty, the input list is investigated. This list contains processes waiting for input from the outside of the stream processor. If this list is also empty, then the gadget program is finished. Otherwise, we do stream-processor input and give the message to all processes in the input list.

scheduler :: Process0 i o
scheduler = 
   do ps@(SS{ freeWire, messageQs, ready, guarded, input }) <- loadSPms
      let (messageQs',guarded',moreReady) = match messageQs guarded
      let run p ready' input' = 
              do storeSPms ps{ messageQs = messageQs'
                             , ready = ready'
                             , guarded = guarded'
                             , input = input'
                             }
                 p
      case (moreReady++ready) of 
         [] -> if null input
                  then nullSPms
                  else do i <- getSPms
                          case [ih i | ih <- input] of
                            p:ready' -> run p ready' []
         p:ready' -> run p ready' input

match ::  MessageQueues -> [Guarded0 i o] 
      ->  (MessageQueues,[Guarded0 i o],[Process0 i o])
match m [] = (m,[],[])
match m (g:f) = case match1 m g of
      Nothing     -> (m',g:f',r) where (m',f',r) = match m f
      Just (m1,p) -> (m2,f',p:r) where (m2,f',r) = match m1 f

match1 :: MessageQueues -> Guarded0 i o 
   -> Maybe (MessageQueues,Process0 i o)
match1 m [] = Nothing
match1 m ((AGuarded0 (Wno w) f):gs) = 
   case IntMap.lookup w m of
       Nothing -> match1 m gs
       Just mq -> case Queue.head mq of
          Msg msg -> Just (m',cast f msg) -- ! type cast !
             where mq' = Queue.tail mq
                   m' = if Queue.null mq' 
                        then delete w m 
                        else modify Queue.tail undefined w m

cast :: a -> b -- Not defined in Haskell.

Figure 83. The scheduler.

The function match applies all guarded processes for which there are matching messages. It returns the remaining unmatched messages and guarded processes, together with a list of new ready processes.

Recall that each element in the field guarded is itself a list, which comes from a call to primRx. The function match1 looks for a matching message for one of the elements in such a list, possibly returning a new message queue and a ready process. A matching message must have the same wire number as the guarded process. It seems like this cannot be expressed in the type system, so we are forced to use a type cast (see the function match1 in Figure 83).

The stateless processes can do stream-processor input/output by means of get0 and put0. The output part is easy:

put0 :: o -> Process0 i o -> Process0 i o
put0 o p = 
   do putSPms (Right o) 
      p

When it comes to input, the process does not directly call getSPms, since that would block other threads as well. Instead, the continuation is put on the input list in the scheduler state, and jump to the scheduler. Note that more than one process may call get0. As we have already seen, the scheduler will ensure that all of them will receive the next message that the stream processor inputs.

get0 :: (i -> Process0 i o) -> Process0 i o
get0 i = 
   do ps@(SS{ input }) <- loadSPms 
      storeSPms ps{ input = i:input }
      scheduler

If a process terminates, we need to schedule some other process for execution if possible. Therefore,


        primTerminate0

simply jumps to the scheduler.

primTerminate0 :: Process0 i o
primTerminate0 = scheduler

To launch a process, the process state must be initialised. This is done in primLaunch0.

primLaunch0 :: Process0 i o -> Process0 i o
primLaunch0 p = 
   do storeSPms SS{ freeWire  = startWno
                   , messageQs = IntMap.empty
                   , ready     = []
                   , guarded   = []
                   , input     = []
                   } 
      p

So far, we have been quite general about the type of messages that our stateless processes will speak. To implement gadget processes, we will use the stream-processor I/O to simulate the keyboard, mouse and screen, as discussed in Section 31.1.1. We will call stateless gadget processes GProcess0.

type GProcess0 = Process0 GEvent GCommand

The types GEvent and GCommand will be defined in Section 31.2.4.

31.2.3 Gadgets processes with state

Now, we have defined most of the necessary primitive operations required for Gadget processes, except for the ones that manipulate a local state. It turns out to be straightforward to add state to GProcess0:

newtype Process s = P ((s -> GProcess0) -> s -> GProcess0)

A stateful process is a process-valued function which takes a stateless process continuation (parameterised over its input state), and an input state as parameters. It can modify the state before applying it to the continuation, and also use the stateless process primitives.

The state parameter is accessed by setState and readState.

unp (P p) = p

setState :: s -> Process s -> Process s
setState a p = P $ \c s -> unp p c a

readState :: (s -> Process s) -> Process s
readState p  = P $ \c s -> unp (p s) c s

We now need to lift the primitive operations of type


        GProcess0

to Process. We use two auxiliary functions, depending on whether the continuation takes an argument or not. (This ``duplication of code'' is a price we pay for not working with monads: in monadic style, all operations return a value, which might be () if it is uninteresting. In CPS, operations without a result take continuations without an argument, which can be seen as a slight optimisation, but adds to the complexity of CPS programming.)

liftP0arg ::  ((a -> GProcess0) -> GProcess0) 
          ->  (a -> Process s) -> Process s
liftP0arg p0 p = P $ \c s -> p0 (\a->unp (p a) c s)

liftP0c ::  (GProcess0 -> GProcess0) 
        ->  Process s -> Process s
liftP0c p0 p = P $ \c s -> p0 (unp p c s)

We also need to lift stateless processes into stateful ones:

liftP0 :: GProcess0 -> Process s
liftP0 p0 = P $ \c s -> p0

The operations for creating a wire and transmitting a message are straightforward to lift.

primWire :: (Wire a -> Process s) -> Process s
primWire = liftP0arg primWire0

primTx :: Out o -> o -> Process s -> Process s
primTx o m = liftP0c $ primTx0 o m

We will also need an auxiliary function to ``downgrade'' a stateful process to a function from state to a stateless process.

down :: Process s -> (s -> GProcess0)
down (P p) s = p (\s' -> primTerminate0) s

When lifting primFrom, we must ensure that the guarded processes get access to the state. Guarded stateful processes are therefore guarded stateless processes parameterised over the state.

type AGuarded s = s -> AGuarded0 GEvent GCommand
type Guarded s = [AGuarded s]

primFrom :: In m -> (m -> Process s) -> AGuarded s
primFrom i p = \s -> primFrom0 i (\m -> down (p m) s)

In primRx, we apply the state to each guarded process, revealing the stateless guarded processes that primRx0 accepts.

primRx :: Guarded s -> Process s
primRx gs = P $ \c s -> primRx0 [g s | g <- gs]

The remaining primitive operations are straightforward to lift.

primTerminate :: Process s
primTerminate = P $ \c s -> primTerminate0

primSpawn :: Process a -> a -> Process s -> Process s
primSpawn p' s p = liftP0c (primSpawn0 (down p' s)) p

primLaunch :: Process s -> s -> GProcess0
primLaunch p s = primLaunch0 (down p s)

31.2.4 Simulating Gadget input/output

To complete the functional implementation of the Gadget primitives, we still must define mouse, screen and keyboard. We use the stream-processor input/output to mediate the events and commands from/to the mouse, keyboard and screen.

data GEvent =    ME MouseEvnt  | KE KeyboardEvnt  | SE ScreenEvnt
data GCommand =  MC MouseCmnd  | KC KeyboardCmnd  | SC [ScreenCmnd]

Each device is controlled by two processes: the output handler, which injects commands received on a wire into the type GCommand and outputs them, and the input handler, which inputs events, extracts those specific for the device and transmit them on a wire. These two handlers run in parallel. This is captured with the deviceHandler.

deviceHandler ::  (c -> GCommand) -> (GEvent -> Maybe e)
              ->  In c -> Out e -> Process s
deviceHandler inj extract cw ew = 
      liftP0 $ primSpawn0 ohandler ihandler
  where ohandler = primRx0 [primFrom0 cw $ \cmd -> 
                            put0 (inj cmd) ohandler]

        ihandler = get0 $ \i -> 
                   case extract i of
                     Just evt  -> primTx0 ew evt $
                                  ihandler
                     Nothing   -> ihandler

We can now form our devices.

keyboard :: In KeyboardCmnd -> Out KeyboardEvnt -> Process s
keyboard = deviceHandler KC (\i -> case i of KE e  -> Just e
                                             _     -> Nothing)

mouse :: In MouseCmnd -> Out MouseEvnt -> Process s
mouse = deviceHandler MC (\i -> case i of ME e  -> Just e
                                          _     -> Nothing)

screen :: In [ScreenCmnd] -> Out ScreenEvnt -> Process s
screen = deviceHandler SC (\i -> case i of SE e  -> Just e
                                           _     -> Nothing)

Outside the Gadget stream processor, the screen commands are transformed into corresponding Fudget drawing commands, whereas the keyboard and mouse control commands are ignored. Conversely, Fudget keyboard presses, mouse clicks and screen exposure events are transformed into GEvent messages. This is done in the fudget gadgetF, of type

gadgetF :: Gadget -> F a b

Note that the high-level streams of gadgetF are unused. It would be nice to use them for communication between gadget processes and the rest of the fudget program, but this is not possible in a type-safe way. The reason is that such a communication could be used to exchange wires between different instances of gadgetF. Each gadgetF has its own scheduler, and mixing wires between schedulers is not type safe.

31.3 Discussion

For the functional programmer, the Haskell implementation of a Gadget scheduler seems attractive. Different scheduling principles can be implemented and compared. Profiling tools can be added, also in Haskell. For example, it might be interesting to see how the wire queue length evolves over time (Figure 84).

Figure 84. Example of wire queue length profiles, provided by the Gadgets-in-Fudgets implementation. Each profile represents one wire, its height is proportional to the length of the queue of messages waiting to be delivered. The picture is a snapshot of the computation; by pressing the button, a new snapshot is taken. The time axis is the one growing into the graph.

A disappointment is that we are not able to safely type check all parts of the scheduler. Nevertheless, we believe that the Haskell implementation is ``more'' type safe than the original scheduler, which was written in C.

The functional scheduler also has a serious performance problem for certain processes. If a process dynamically creates wires, sends messages to them, and then forgets them, the wire queues cannot be garbage collected. The functional scheduler can never know if a process drops its reference to a wire.

A remedy for these problems is to use lazy state threads [LJ94] and their imperative variables for representing the queues.

V Applications

One strong motivation behind the development of Fudgets was practical usefulness, that is, we wanted to be able to write serious applications with graphical user interfaces in a declarative style, in a pure functional language. Hand in hand with the development of the library, we have therefore developed a number of small and large applications.

To give you some idea of what the potential of the fudget library is, and to discuss various practical programming considerations, this part presents, in varying detail, some applications we have implemented using Fudgets.

32 WWWBrowser -- a WWW client

A good example of an application that makes full use of all aspects of the Fudget library is a World-Wide-Web client. It displays hyper-text documents with embedded images and GUI elements (to implement fill-in forms). The documents are obtained from various information sources on the Internet through protocols like ftp, nntp, gopher and http.

In this section we will take a look at how such an application can be implemented on top of the Fudget library, in Haskell. An actual implementation, called WWWBrowser, was done mainly during the summer 1994. Some updates and improvements were made in the summer 1997. A window snapshot is shown in Figure 85.

Figure 85. WWWbrowser, a simple web browser implemented using fudgets in 1994. It supports inlined images and forms.

The 1994 version of WWWBrowser had the following features:

It accepted most of HTML 2.0 (the HTML standard in use in 1994), including
- fill-in forms.
- inlined images (file formats: gif, jpeg, xbm, pnm).
It supported the usual protocols: http, gopher, ftp, news, local files/directories.
It fetched multiple inlined images in parallel. This made WWWBrowser faster than Mosaic (the most widely used browser in 1994) when fetching pages with many small images.
It simplified copy and paste of URLs. You could mark a URL in, e.g., a text editor and then click with the middle mouse button in the browser window to view that page.

Some quick facts about the 1994 implementation:

The HTML input was parsed into an abstract syntax tree, which was then converted in several stages into drawing commands producing text with the appropriate layout, font and other attributes. This was done using fudget kernels (see Section 22.1.2) written specifically for this purpose.
The HTML parser was implemented using the fairly efficient, backtracking parsing combinators developed by Niklas Röjemo [Röj95a] for use in his Haskell compiler. To improve the tolerance of bad HTML, an extra tag balancing pass was added between the lexical analyser and the parser, but the parser still failed on some web pages.
Form elements and images were implemented as ordinary fudgets, placed appropriately in the text. (Their sizes affect the layout.)
Image conversion (e.g., decompressing gif and jpeg) was done by calling external programs (giftoppm, etc.).
Image processing (color remapping and, optionally, dithering) was done in Haskell.
Program size: approximately 4000 lines of Haskell.
Implementation time: approximately 1 man month.

The following was changed and added in 1997:

The source code was translated from Haskell 1.2 to Haskell 1.4.
The parser was rewritten using a version of Swierstra & Duponcheel's deterministic, error-correcting parsing combinators [SD96]. This parser turned out to be more elegant (the extra tag balancing pass could be removed) and more tolerant to bad HTML. At the same time, the parser was updated to accept most of HTML 3.2 [Eng97]. The new parser ran at roughly the same speed as the old one.
The rendering was done by translating the HTML into a Drawing (see Section 27.4), using a function of the type Html -> Drawing ... (roughly). The old tailor made fudget kernels were thrown out. The fudget library placer tableP was be used to add support for tables (the table cell attributes rowspan and colspan were not supported yet).
The fudget layout system was improved with the capabilities to do paragraph filling and adjust the layout according to the width of the window (see Section 27.6).
Support for background colors and background images was added.
Support for fetching documents via a proxy was added. (A proxy is a server that relays document requests. Most WWW browsers can be configured to fetch all documents via a proxy instead of fetching them directly from the server that has the document.)
Image fetching, conversion and processing was moved to a separate process, allowing the text of a page to be displayed and be sensitive to clicks before the images have been loaded. Part of the page may be redrawn when the size of an image becomes known. (With a parallel implementation of fudgets, you would get this for free. )
Experimental support for fupplets (functional a pplets) was added. Fupplets are applets written in Haskell using the Fudget library.
WWWBrowser can now read the bookmark file created by Netscape [Netb] and display it in a hierarchical menu.
The program size now is approximately 4500 lines.

32.1 Overall structure of the current WWW browser implementation

WWWBrowser is implemented in a straight-forward way. The key data types are, not surprisingly, URL and


      Html

. The key operations on these types are:

data URL = ...
data Html = ...

parseURL  :: String -> Maybe URL
showURL   :: URL -> String
joinURL   :: URL -> URL -> URL

parseHtml    :: String -> Either ErrorInfo Html
drawHtmlDoc  :: URL -> Html -> HtmlDrawing
type HtmlDrawing = Drawing ... -- details in Section 32.3

Documents are fetched from their location on the web by the fudget urlFetchF,

urlFetchF :: F HttpRequest HttpResponse     -- details in Section 32.2

data HttpRequest   = HttpReq   { reqURL::URL, ... }
data HttpResponse  = HttpResp  { respBody::String, ... }

The fudget urlFetchF handles several protocol besides the HTTP protocol, but since HTTP is the primary protocol on the WWW, it was the one that was implemented first. The fudgets for other protocols were then implemented with the same interface.

Documents are displayed by the fudget htmlDisplayF,

htmlDisplayF :: F (URL,Html) HttpRequest

which displays HTML documents received on the input, and outputs requests for new documents when the user clicks on links in the document being displayed.

Not all documents on the WWW are HTML documents. Other types of documents (for example plain text, gopher pages, ftp directory listings and Usenet news articles) are handled by converting them to HTML:

toHtml :: (URL, HttpResponse) -> (URL,Html)

The function toHtml uses parseHtml and other parsers.

Using the components presented above we can create a simple web browser by something like

simpleWebBrowser =
  loopF (htmlDisplayF >==< mapF toHtml >==< urlFetchF)

But in addition to the HTML display, WWWBrowser provides back/forward buttons, an URL-entry field, a history window, a bookmarks menu, a document source window and a progress report field. The structure of the main fudget is shown in Figure 86. The layout is specified using name layout (see Section 11.2).

wwwBrowserF =
    httpMsgDispF >==<
    loopThroughRightF urlFetchF' mainGuiF >==<
    menusF
  where
    mainGuiF = urlInputF >*< srcDispF >*<
               (urlHistoryF >*< htmlDisplayF) >=^< toHtml

    httpMsgDispF =
      nameF "MsgDisp" $ "Progress:" `labLeftOfF` displayF

    urlFetchF' = post >^=< urlFetchF >=^< stripEither
      where
        post msg = ...

    urlInputF = ... parseURL ... stringInputF ... showURL ...

    srcDispF = ...

    urlHistoryF = ...

Figure 86. wwwBrowserF -- the main fudget in WWWBrowser.

32.2 Implementing Internet protocols

The fudget urlFetchF is implemented as a parallel composition of fudgets handling the different protocols. This is shown in Figure 87. The function distr extracts the protocol field from the request URL and sends the request to the appropriate subfudget.

urlFetchF :: F HttpRequest HttpResponse
urlFetchF = snd >^=< listF fetchers >=^< distr
  where
    fetchers =
      [("file",fileFetchF>=^<reqURL),  -- local files and ftp
       ("http",httpFetchF),            -- http and gopher requests
       ("news",newsFetchF>=^<reqURL),
       ("telnet",telnetStarterF>=^<reqURL)
      ]
    distr req@(HttpReq {reqURL=url}) = (fetcher,req)
      where
        fetcher = ...

Figure 87. The fudget urlFetchF.

The implementation of the individual protocol fudget kernels are written in continuation style. For the http protocol, the following operations are performed:

A request is received in a high-level input.
The host field of the URL is extracted and a socket connection to that host is opened. If a proxy is used, a connection to the proxy is opened instead.
The request is sent to the host (or the proxy).
The reply is received in chunks (see Section 14.1) and assembled and the connection is closed.
If a redirection response was received, the process is restarted from step 2 with the redirection URL.
If a normal or an error response was received, it is put in the high-level output stream.

The implementation of the NNTP (news) protocol is similar. A difference is that the NNTP protocol can handle several requests per connection, so the connection is kept open after a request is completed, so that it can be reused if the next request is directed to the same host. This is usually the case, since you normally fetch all news articles from the same, local news server. (It is possible, but uncommon, to specify a particular news server explicitly in the URL.)

The FTP protocol can also handle several requests per connection, and since you are required to log in before you can transfer files, it is even more beneficial to reuse connections.

The FTP protocol differs in that it uses a control connection for sending commands that initiate file transfers and a separate data connection for each file transfer. The data connection is normally initiated by the server, to a socket specified by the client. In the fudget implementation, these two connections are handled by two separate, but cooperating, fudgets.

32.3 Displaying HTML

HTML documents contain a sequence of elements, which are delimited by tags. Elements can contain plain text and other, nested elements. For example,

<H1>The fudget <TT>htmlDisplayF</TT></H1>

is an element tagged as a top-level heading, and it has a nested element marked to be displayed with a typewriter font.

There is a distinction between block-level elements and text-level elements. The former mark up text blocks that are to be treated as complete paragraphs. They are thus composed vertically. Heading elements are examples of block-level elements. The latter mark up arbitrary sequences of characters within a paragraph. Block-level elements can contain text-level elements (as in the example above), but not vice versa.

WWWBrowser makes use of the distinction between block-level and text-level elements. This makes it easier to do the layout. The function parseHtml builds a syntax tree which on the top level is a sequence of block-level elements. Plain text occuring on the top level, outside any block-level element, is understood as occuring inside an implicit paragraph (<P>) element. So, for example,

<H1>The fudget <TT>htmlDisplayF</TT></H1>
The implementation of...

is parsed into the same syntax tree as as

<H1>The fudget <TT>htmlDisplayF</TT></H1>
<P>The implementation of...</P>

With this approach, the function


      drawHtmlDoc

can simply recurse down the syntax tree, composing the drawings of block-level elements using verticalP and text-level elements using paragraphP.

Web pages contain not only text, but also images and form elements. In WWWBrowser, these are implemented by embedding fudgets in the drawing. We introduce the type ActiveDrawing for drawings containing active components and define the type HtmlDrawing introduced above as

type HtmlDrawing = ActiveDrawing HtmlLabel Gfx HtmlInput HtmlOutput

type ActiveDrawing lbl leaf i o = Drawing lbl (Either (F i o) leaf)

where HtmlInput and HtmlOutput are the message types used by the fudgets implementing images and forms. Elements with special functionality are marked with a label of type


      HtmlLabel

. Currently, hyperlinks, link targets, forms and image maps are labelled.

To display ActiveDrawings, a generalisation of graphicsF (see Section 27.5.1) has been defined:

activeGraphicsF ::
  F (Either (GfxCommand (ActiveDrawing lbl leaf i o)) (Int,i))
    (Either GfxEvent (Int,o))

The fudget htmlDisplayF uses activeGraphicsF to display HTML documents. It also contains

a stream processor that collects the contents of form elements and generates the appropriate HttpRequest when the submit button of a form is pressed.
an instance of the fudget imageFetchF (described below) that the image fudgets communicate with to obtain the images they should display.

32.4 Fetching images in parallel

Images in HTML documents are included by reference using URLs and are fetched from their sources separately. The fudget


      htmlDisplayF

uses the fudget imageFetchF for this:

imageFetchF :: F ImageReq (ImageReq,ImageResp)

type ImageReq   = (URL,Maybe Size)
type ImageResp  = (Size,PixmapId)

The requests handled by imageFetchF contain the URL of an image to fetch and an optional desired size to which the image should be scaled. The responses contain the actual size (after scaling) and a pixmap identifier.

Since documents may contain many images and the time it takes to fetch an image often is dominated by network latency rather than bandwidth limitations, it makes sense to fetch several images in parallel. The fudget parServerF,

parServerF :: Int -> F req resp -> F req resp

is a generic fudget for creating servers that can handle several requests in parallel. If serverF is a fudget that handles requests sequentially with a 1-1 correspondence between requests and responses, then the fudget

parServerF 
      n serverF

handles up to n requests in parallel.

Clients of parServerF must have some way of telling which response belongs to which request, since the order in which the responses are delivered is not guaranteed to correspond to the order in which the requests are received. The fudget imageFetchF accomplishes this by including the requests in the responses.

We also want to avoid fetching the same image twice. This is solved by using a caching fudget,

cacheF :: Eq req => F req (req,resp) -> 
                    F (client,req) (client,(req,resp))

In addition to caching responses, it keeps track of multiple clients and avoids sending the same request twice to the server even if two clients send the same request at the same time. (This situation arises easily in htmlDisplayF, since it is common for the same image to occur in several places in the same HTML document.)

In WWWBrowser, a composition like this is used to fetch images:

cacheF (parServerF 5 imageFetchF)

The implementation of parServerF is shown in Figure 88. The implementation of cacheF is shown in Figure 89.

parServerF :: Int -> F req resp -> F req resp
parServerF n serverF =
    loopThroughRightF (absF ctrlSP0) serversF
  where
    serversF = listF [(i,serverF) | i<-ns]   -- n parallel servers
    ns = [1..n]                              -- server numbers

    ctrlSP0 = ctrlSP ns

    -- The argument to ctrlSP is a list of currently free servers
    ctrlSP servers =
        case servers of
          -- If all servers are busy, wait for a response.
          []          -> getLeftSP $ fromServer
          -- If there is a free server:
          s:servers'  -> getSP $ either fromServer fromClient
            where
              fromClient req =
                -- When a requests is received, send it to the
                -- first server in the free list and continue
                -- with the remaning servers still in the free list.
                putSP (Left (s,req)) $ ctrlSP servers'
      where
        fromServer (n,resp) =
          -- When a response is received from a server
          -- output it and add the server to the free list.
          putSP (Right resp) $ ctrlSP (n:servers)

Figure 88. The fudget parServerF.

cacheF :: Eq req => F req (req,resp) -> F (client,req) (client,(req,resp))
cacheF serverF = loopThroughRightF (absF (cacheSP [] [])) serverF

cacheSP cache pending =
    getSP $ either answerFromServerSP requestFromClientSP
  where
    requestFromClientSP (n,req) =       -- A request from client n.
        assoc oldSP newSP cache req
      where
        oldSP ans =     -- The answer was found in the cache.
            putSP (Right (n,(req,ans))) $
            cacheSP cache pending

        newSP =         -- A new request, send it to the server, and
                        -- add the client to the pending list.
            if req `elem` map snd pending
            then cont
            else putSP (Left req) cont
          where
            cont = cacheSP cache ((n,req):pending)

    answerFromServerSP ans@(req,_) =
                -- The server delivered an answer to request req,
                -- save it in the cache,
                -- forward it to waiting clients and remove them from
                -- the pending list.
        putsSP [Right (n,ans) | (n,_)<-ready] $
        cacheSP (ans:cache) pending'
      where
        (ready,pending') = part ((==req).snd) pending

Figure 89. The fudget cacheF.

32.5 Discussion

A drawback with WWWBrowser, as compared to other modern browsers, is that it does not display documents incrementally as they are received from the network. This is due to several facts:

The current design of urlFetchF does not output anything until it has received the complete document.
Even if urlFetchF was changed to output chunks as they are received, you would have to concatenate all the pieces before you apply the function parseHtml to it.
The fudget htmlDisplayF is implemented with graphicsF. When graphicsF receives a new drawing to display, it computes its size and adjusts the window size accordingly before it draws anything in the window. This means that it needs the complete drawing before it can display anything.

One way of achieving incremental display of received documents would be to let urlFetchF output a response containing the document as a lazy list of characters as soon as it begins receiving it from the server. This would allow you to apply the parser and the drawing function immediately and send the resulting drawing to graphicsF. The parser


      parseHtml

and drawing function drawHtmlDoc must be carefully constructed to be lazy enough to produce some output even when only an initial fragment of the input is available. You would also have to change graphicsF so that it does not start by computing the size of the drawing. It should instead lazily compute drawing commands (see Section 27.2) to send to the window system. The size of the window should be adjusted regularly according to where the drawing commands generated so far have drawn.

The above solution seems to require the introduction of some mechanism for indeterministic choice, since while the drawing commands for the document are being computed and output, the program should to continue to react to other input.

However, the trend in I/O systems for functional languages goes towards making I/O operations more explicit. Even the Fudget library has abandoned the representation of streams as lazy lists in favour of a simpler deterministic implementation. Using a lazy list for input as above is thus a step in the opposite direction. However, to program indeterministic systems on a high level of abstraction, streams as lazy lists seem to be useful.

One can of course think of ways of achieving incremental display without doing input in the form of lazy lists.

We could let urlFetchF output chunks of characters as they become available.
We could create a parsing library that creates parsers in the form of stream processors. The type of the function parseHtml would then be SP String Html instead of String -> Html. However, we will not achieve incremental display if we continue to output the syntax tree of whole document in one message. We would instead have to output a sequence of document fragments.
The input of the fudget htmlDisplayF would be document fragments instead of complete document. We are thus moving one step in the direction of an HTML editor instead of a simple display.

But it does not seem like good software engineering to have to create a different parsing library just because we want to use the constructed parsers in an interactive program, but sticking to the philosophy behind the Haskell I/O, it seems that this is what we would have to do.

The conclusion we draw from this is that the current I/O system in Haskell does not integrate well with laziness.

33 Alfa -- a proof editor for type theory

Alfa is a WYSIWYG proof editor. It allows you to, interactively and incrementally, define theories (axioms and inference rules), formulate theorems and construct proofs of the theorems. All steps in the proof construction are immediately checked by the system and no erroneous proofs can be constructed. The logical framework used is one of Thierry Coquand's versions of Per Martin-Löf's Type Theory.

Alternatively, you can view Alfa as a syntax-directed editor for a small purely functional programming language with a type system that provides dependent types. The editor immediately checks that programs you enter are syntactically correct and type correct.

Alfa is largely inspired by Window-Alf [AGNvS94], implemented by Lena Magnusson and Johan Nordlander, and has a similar user interface.

The plan is that Alfa should improve on Window-Alf by

allowing the user to define how proof terms should be presented on the screen (and on paper). This includes simple things like argument hiding and infix operators, but also more advanced mathematical notation and natural deduction style proof trees and other representations of proofs. Alfa should also allow you to produce documents where explanatory text and proof fragments are interleaved.
using ideas from hypertext and Web browser to allow the user to efficiently navigate through large proofs and libraries.

Some of this has been implemented. As shown in Figure 90, proofs can be presented in natural deduction style.

Figure 90. Window dump of Alfa, illustrating the construction of a simple proof in natural deduction style.

Whereas Window-Alf was implemented in Standard ML (proof engine) and C++ & Interviews (user interface), Alfa is implemented entirely in Haskell, using Fudgets for the user interface. At the time of writing, the source code consists of about 8000 lines, distributed as follows:

The proof engine by Thierry Coquand. 2700 lines. This includes a parser and parser combinators (480 lines).
Extensions and improvements of the Fudget library. 1900 lines. The largest part of this is the new fudgets for displaying structured graphics (described in Chapter 27) and syntax-directed editing. It also includes a new file-selection window and a string-entry window with immediate syntax checking and feedback via a smiley (see Figure 91). Although the development of these were prompted the Alfa project, they are general enough to be used in other contexts.
Figure 91. The smiley indicates whether there is a syntactic error in the input.
The Alfa User Interface. 3400 lines. The largest parts are the implementation of the WYSIWYG style editing operations (1000 lines) and the code for drawing/building abstract syntax trees used by the syntax-directed editor fudget (800 lines).

In addition, Aarne Ranta has supplied 2100 lines with support for natural language. Some of this code had been integrated in Alfa, but this work was in a rather experimental stage.

More detailed and up-to-date information on Alfa is available on the WWW [Hal97].

34 Humake -- a distributed and parallel make tool for Haskell

Humake is a tool for compiling Haskell programs. It allows independent modules to be compiled in parallel, possibly on different computers. It has a graphical user interface (see Figure 92) where the progress of the compilation can be monitored and information on individual modules can be obtained. The module-dependency graph is automatically extracted from the source code. The dependency graph, file-modification dates and other module information is retained between compilations and can be dynamically updated when a module is changed, to minimise the work required to start a recompilation and thus make the edit-compile-test development cycle faster.

Figure 92. The user interface of Humake.

In the current version, the user interface shows

a module list where the status of each module is indicated by a colored lamp. The color is green if the module is up-to-date, yellow if it is being compiled or waiting to be compiled (because it is out of date with respect to its source code or the interface of an imported module), red if compilation of the module failed and blue if the module was taken from a pre-compiled library. A menu allows you to choose from a number of different sorting orders.
a module information window, which shows imported modules, modules that import this module, file location and modification dates.
an update button which makes Humake re-read the module information after it has been changed. Humake can also receive change notifications directly from a text editor. This has been implemented for Emacs.
a list showing which modules are currently being compiled and how many modules are currently waiting to be compiled.

34.1 Implementation

The structure of the implementation is sketched in Figure 93. Most of the work is handled by the fudget dependencyF. It traverses the modules to extract the module-dependency graph and builds a representation of it. It also maintains a data structure representing the status of the compilation process. This structure is chosen so that when a compilation completes, or a module is updated, a new compilation can be started as quickly as possible.

The source is about 1200 lines long.

main = fudlogue $ shellF "Humake" humakeF

humakeF =
  loopLeftF ((moduleInfoF>+<parallelCompileF) >==< dependencyF)
    >==< editorInterfaceF


--- GUI fudgets:

statusDisplayF = ... --the bottom part of the window

moduleInfoF = ... -- the module list, module info and the update buttons


--- Non-GUI fudgets:

parallelCompileF =
    filterRightSP >^^=< (statusDisplayF>+<idF) >==<
    loopThroughRightF (absF ctrlSP) (parServerF hosts compileF)
  where
    ctrlSP = ...

parServerF :: [id] -> (id->F req resp) -> F req resp
parServerF ids serverF = ... -- essentially as in Figure 88

compileF :: String -> F CompilerReq CompilerResp
compileF host = ... -- a compilation server

editorInterfaceF :: F a String
editorInterfaceF = ... -- outputs the name of a file when it is saved

Figure 93. Implementation of Humake.

35 Space Invaders -- real-time and simulation

This section illustrates how the Fudget system can be used to write real-time interactive games. This shows that the Fudgets GUI toolkit is not limited to traditional, fairly static, graphical user interfaces, but also allows you to construct interfaces with lots of animated objects. By structuring the program with one concurrent process (one fudget) per animated object the program can be seen as a model that simulates some real-world objects and the way they communicate.

35.1 Space Invaders

We start with a brief description of the classical game Space Invaders. Only the most fundamental parts of the game have actually been implemented.

Figure 94. Space Invaders -- a typical interactive real-time game.

In this game, an army of invaders from outer space is approaching the earth. The player must shoot them all down before they reach the surface. Some points are added to the player's score for each invader that is shot down. The player controls a gun, which can be moved horizontally at the bottom of the screen (the surface of the earth) and which can fire vertically. The invaders initially move from left to right. When the right-most invader reaches the right edge of the screen all invaders first move downwards a small distance, then move horizontally again until the left-most invader reaches the left edge, and so on.

35.2 Structure of the Space-Invaders implementation

In this section we describe an implementation of Space Invaders, where the each object is implemented as a fudget. The objects are:

spaceF: the space fudget. This is the black background in which all the other objects move around.
gunF: the gun.
torpedoF: the torpedoes fired by the gun.
invaderF: a number of invaders

There is also scoreF, which displays the current score and a high-score. gunF and torpedoF use timers internally to control the speed of their motion. To coordinate the motion of the invaders, they are controlled by a common timer which is located in a windowless fudget called tempoF. There is also an abstract fudget called shoutSP, which broadcasts timer alarms and other input to all invaders.

Section 35.2 illustrates how the fudgets are interconnected. The information flow is as follows: the space fudget outputs mouse and keyboard events to gunF. (This allows the user to place the mouse pointer anywhere in the window to control the gun.) The gun responds to these events by starting or stopping its movement, or by firing a torpedo. When the gun is fired, it outputs its current position to the torpedo fudget. The torpedo then starts moving upwards from that position. When it hits something, it outputs its current position to the invaders. Each invader then checks if the hit is within the area it occupies on the screen and, if so, it removes its window and dies.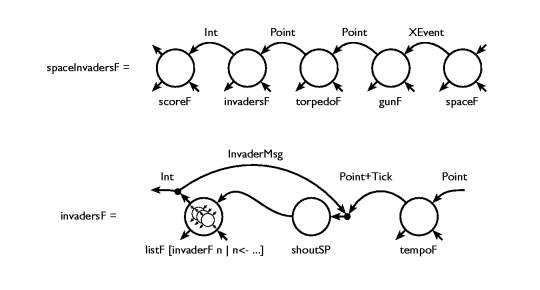

Figure 95. The processes and their interconnection in the Space-Invaders implementation.

Below, we take a closer look at invaderF. The other fudgets are just variations on a theme, so we will not discuss them further.

The fudget invaderF maintains an internal state consisting of the following parts: the current position (a Point), the current direction (left or right), if it is time to turn (i.e., move downward at the next timer alarm, and then change directions).

The invaders speak the following language:

data InvaderMsg = Tick | Turn | Hit Point | Death (Int,Int)

When an invader hears a Tick, it moves one step in the current direction. It also checks if it has reached an edge, in which case it outputs Turn, which is received by all invaders. When an invader hears a Turn it remembers that it is time to turn at the next Tick. When a torpedo has hit something at position p, all invaders receive Hit p, and check if p is within their screen area. If so, it outputs Death n, where n is the identity of the invader. This identity is recorded by shoutSP, so that it does not have to shout to dead invaders. It is also used to determine how many points to add to the score.

The fact that all objects are implemented as group fudgets means that each object has its own X window. To move an object you move its window. No drawing commands need to be output.

How does the torpedo know if it has hit something? The torpedo is a window which moves behind all other windows. This means that it becomes obscured when it hits something. The X server sends a VisibilityNotify event when this happens. This causes the torpedo to stop and send its current position to the invaders. (Nice hack, isn't it? But isn't there a timing problem? And what if the torpedo is obscured by some other application window? We leave it to the reader to ponder over this.)

35.3 About the efficiency of the Space-Invaders implementation

One major point of the Fudget system (and of functional programming in general) is to simplify and speed up program development. But it is of course also important that the efficiency of the resulting program is acceptable.

We have measured the CPU time consumption of the Space-Invaders implementation described above running on a Sparcstation IPX in a situation where 55 invaders move twice per second, the gun and the torpedo move every 30ms. The average CPU load was approximately 60%. 10% of this was consumed by the X server. As a comparison, the program xinvaders, a C program implemented directly on top of Xlib, consumes less than 5% CPU time in a similar situation.

As usual, programming on a higher abstraction level results in a less efficient solution. Part of the inefficiency comes from the use of Haskell and the Fudget system. The load on the X server comes from the fact that the moving objects are represented as windows. Not surprisingly, moving a window is a more expensive operation than just drawing an image of the same size. But using techniques outlined in the next section, it is possible to rewrite the Fudget program to draw in a single window, like the C program, and still keep the same nice program structure, i.e., one process per moving object.

Above, we compared the efficiency of a high-level implementation (using the Fudget system) of the game with a low-level implementation. It would also be interesting to compare other user interface toolkits, e.g. Motif and Interviews, to the Fudget system.

The CPU time consumption figures above do not say much about the real-time behaviour of the two implementations. The fact is that the C program meets the real-time deadlines, but the Fudget program does not. As a response to a Tick from tempoF, all 55 invaders should move one step. Computing and outputting 55 MoveWindow commands unfortunately takes longer than 30ms, which means that the MoveWindow commands for the gun and the torpedo will be output too late, resulting in a jerky motion. This problem can be solved in at least two different ways: manually, by not moving all 55 invaders at the same time and thus not blocking output from other fudgets for longer than 30ms; automatically (from the point of view of the application programmer), by introducing parallel evaluation and some kind of fair, indeterministic merge of the output from different fudgets. The latter solution is of course the more general one, and we hope to improve the Fudget system in this direction.

35.4 Replacing fudgets with stream processors for efficiency

Above, we outlined a program structure where each moving object on the screen is represented as fudget with an associated window on the screen. It is of course possible to use fudgets for other kind of simulations where the objects do not correspond to user interface elements.

The behaviour of a single fudget is usually implemented as a sequential program by using the stream-processor operators putSP, getSP and nullSP. To increase the efficiency of our space invaders implementation, we can instead structure the program as one fudget whose behaviour is described by some composition of stream processors. This increases the efficiency in two ways:

The communication between stream processors is cheaper (less tagging/untagging).
The number of windows is reduced. This means that conversions between paths and window identifiers in fudlogue (Section 22.2.2) will be somewhat cheaper, and that the load on the X server is reduced (since windows will not be moved).

In Section 35.2 the input to the invaders is broadcast to all invaders. We implemented this using listF (tagged parallel composition) and a separate stream processor shoutSP. Some overhead can be avoided by using untagged parallel composition of stream processors instead:

-*- :: SP a b -> SP a b -> SP a b

This also makes it easy to write stream processors that dynamically split into two or more parallel processes. One of the processes in a parallel composition can terminate without leaving any overhead behind, since

nullSP -*- sp == sp -*- nullSP == sp

Doing the same with processes represented as fudgets would not give you the same efficiency advantage since the low-level streams remain tagged even in untagged parallel compositions. Thus when one process in a parallel composition terminates, some tagging overhead will remain.

The fact that parallel compositions can reduce to nullSP gives us an opportunity to make use of the sequential composition operator seqSP (Section 16.4) in an interesting way. Suppose that all that is needed to start a new level in the game is the creation of a new army of invaders. Then the behaviour of the game could be programmed in the following way:

playGameSP = playLevelSP 1

playLevelSP level = startNewLevelSP level `seqSP` playLevelSP (level+1)

startNewLevelSP level = invaderArmySP level

invaderArmySP level = ... -- creates a parallel composition of invaders

When the last invader in the invader army dies, the parallel composition will be reduced to nullSP, which causes seqSP to invoke the next level.

36 FunGraph

FunGraph is a prototype implementation of a typed visual programming environment, inspired by the commercial product ProGraph.

A screen dump of FunGraph is shown in Figure 96. Basically, FunGraph is a free-form spread sheet with types, where the user can place and connect objects such as cells, sliders and graphs at will. The objects have input connectors on top, and output connectors below.

FunGraph was developed before the fudget graphicsF of Section 27.5.1 was implemented. Instead, graphics where implemented with fine grained fudgets, so to speak. Each object is implemented with a number of fudgets. So each pin is a separate fudget, for example. The objects reside in a dynListF placed in a group window which controlled the wires. All messages from the output pins of the objects are routed by the group window's kernel and looped back into the dynListF, so that the values seem to follow the wires.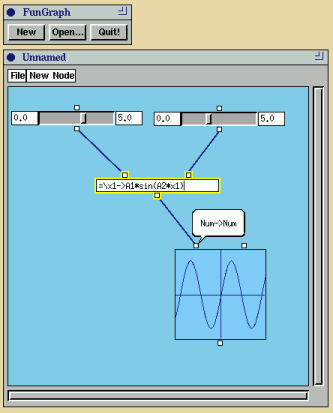

Figure 96. A screen dump of the program FunGraph. Two sliders controls amplitude and frequency of a sine function defined in a cell. This function is then visualised in a graph. The bubble window (implemented by bubbleRootPopupF) shows the type of the pin that the user points at for the moment, which happens to be the left input pin of the graph object. It has the type Num -> Num, which is the type of the functions that the graph object can display.
The cell also shows the visual effect of one of the filter fudgets in the library, which is called the shapeGroupMgr. The cell is currently being selected, which is indicated by a yellow, glowing border around it. This effect is achieved by wrapping a shaped window whose border tightly follows the fudgets inside it (in this case three pin fudgets and one stringF). The border of the shaped window is yellow, and its width is set to zero when the object is deselected, or a couple of pixels as is the case with our cell. The shapeGroupMgr ensures that the shape of the yellow-border window tightly follows the contour of the wrapped fudgets by analysing the ConfigureWindow commands that they output.

37 A mobile data communication protocol prototyping tool

In collaboration with Carlstedt Research & Technology AB and Eritel AB, we developed a prototyping tool for testing and modelling communication protocols in the mobile data network Mobitex. A screen dump of the tool is found in Figure 97, and shows a configuration with three radio base stations, each which covers a triangular area. The small circular objects are mobile users. Roaming of the users between base station areas is simulated using the drag-and-drop feature from Chapter 25.

Figure 97. The user interface of the protocol prototyping tool.

38 Two board games

We have implemented two board games, Explode (Figure 98) and Othello (Figure 99) using Fudgets.

The two games use the same underlying combinators for implementing the board. The first is a button that can display changing graphics:

boardButtonF ::  (ColorGen bgcolor, Graphic gfx) =>
                 bgcolor -> Size -> F gfx Click
boardButtonF bg size =
  buttonF'' (setBgColor bg) (g (blankD size)) >=^< Left . setLabel . g

where buttonF'' is the dynamically customisable (see Section 30.3) version of buttonF and setLabel is a customiser that changes the button label.

The second combinator is boardF,

type Coord = (Int,Int)

boardF :: Coord -> (Coord -> F a b) -> F (Coord,a) (Coord,b)
boardF (w,h) squareF =
  placerF (matrixP w) $
  listF [((x,y),sqF (x,y)) | y<-[0..h-1],x<-[0..w-1]]

which, given the size of the board and a function from the coordinates of a square to a fudget implementing that square, creates a parallel composition of square fudgets with the appropriate layout. The square fudgets are addressed with their coordinates.

Figure 98. The Explode game.

Figure 99. The Othello game.

38.1 The Explode Game

Before the 1995 GUI Festival in Glasgow, a workshop on graphical user-interface toolkits and functional programming [Car95], a number of programming challenges were distributed to the participants. One of the challenges was to implement the Explode game.

In the Explode game, two players take turns placing stones, or atoms, in the squares of a board. A player can not place atoms in a square that already contains atoms from the opponent. When a square is full, that is, contains as many atoms as it has neighbours, it explodes, sending one atom to each neighbour. All atoms of the invaded square change color to the invading atom's color. Invaded squares may become full and explode in turn. When the board has settled, a new move can be entered. When the board starts to get full of atoms, placing a new atom may cause an infinite chain reaction. When this happens, the game is over and the player who caused it is the winner.

38.1.1 The Fudgets implementation of the Explode game

The Fudgets implementation of the Explode game was done as shown in Figure 100.

main = fudlogue (shellF "Explode" explodeBoardF)

explodeBoardF =
    loopF (absF routeSP >==< boardF boardSize boardSize atomsSquareF)
  where
    routeSP = concatMapAccumlSP route White
    route side (src,msg) =
      case msg of
        ClickedWhileEmpty -> (otherSide side, [(src,side)])
        ClickedWithColor side' ->
          if side'==side
          then (otherSide side, [(src,side)])
          else (side, []) -- illegal move
        Explode dsts side' -> (side, [(dst,side')|dst<-dsts])

    atomsSquareF :: Coord -> F AtomColor (SquareEvent Coord)
    atomsSquareF (x,y) =
        loopThroughRightF (absF ctrlSP) atomsButtonF
      where
        ctrlSP = concatMapAccumlSP ctrl (0,Nothing)
        ctrl s@(oldcnt,oldside) msg =
          case msg of
            Left Click -> (s,[Right (case oldside of
                                       Just side  -> ClickedWithColor side
                                       Nothing    -> ClickedWhileEmpty)])
            Right side ->
              let cnt=oldcnt+1
              in if cnt>=size
                 then become (cnt-size) side (explodemsgs side)
                 else become cnt side []

        become cnt side msgs = ((cnt,optside),Left (cnt,side):msgs)
          where optside = if cnt==0 then Nothing else Just side
        size = length neighbours
        explodemsgs = (:[]) . Right . Explode neighbours
        neighbours = filter inside2d [(x-1,y),(x+1,y),(x,y-1),(x,y+1)]
        inside2d (x,y) = inside x && inside y
        inside x = 0<=x && x<boardSize

        atomsButtonF :: F (NumberOfAtoms,AtomColor) Click
        atomsButtonF = boardButtonF bgColor sqsize >=^< drawAtoms

        drawAtoms (count,color) = ... -- 20 lines

Figure 100. Fudgets implementation of the Explode game.

Comments:

The loop on the top level together with routeSP allow all square fudgets to communicate with each other. However, each square knows its coordinates and send messages only to its neighbours. The actual communication structure is thus not directly reflected in the program structure.
routeSP also acts as a referee. It keeps track of whose turn it is, to be able to discard illegal moves. This is also where you would put a test for explosions involving all squares (which should end the game). Otherwise, all the work is done by the squares themselves.
Square fudgets receive input when they are invaded by an atom. Square fudgets produce output in the type SquareEvent:
```
data SquareEvent dest
    =  ClickedWhileEmpty
    |  ClickedWithColor AtomColor
    |  Explode [dest] AtomColor
```
where the messages mean
- ClickedWhileEmpty "I was clicked and I was empty". routeSP then replies with an atom of the appropriate color (depending on whose turn it is).
- ClickedWithColor color: "I was clicked and my color was color". If the color matches with color of the current player, routeSP replies with an atom of that color, otherwise the message is ignored (some indication of an illegal move could be produced).
- Explode square color: "I explode and invade square with color". routeSP forwards the message to the square at square. 2-4 messages of this kind are sent when a square explodes.
The square fudgets also communicates with the internal atomsButtonF.
The auxiliary function drawAtoms in atomsButtonF produces the appropriate graphical image for a square, using the types FlexibleDrawing and Drawing described in Chapter 27.

38.1.2 A comparison of the Fudgets and Gadgets versions of the Exlode Game

The submitters of the Explode challenge also provided a solution using Gadgets (see Section 41.3.1). Their solution (see section 6 in [NR95]) is similar to ours in that the effects of the users' moves are computed by message passing between processes representing the squares of the board. In both solutions, there is a separate referee process that, for example, keeps track of whose turn it is to move.

In the Fudgets solution, the squares are in effect connected to all other squares, whereas in the Gadgets solution, each square process is connected through wires only to its neighbours. As noted in [NR95], combining fudgets to achieve exactly this connectivity would be difficult, and it would probably also be difficult to add new processes to such a solution.

As described above, in the current Fudgets solution, each square fudget knows its coordinates and computes the coordinates of its neighbours. It would of course be possible to parameterise the square fudgets by an abstract representation of the neighbours instead,

atomsSquareF :: [address] -> F AtomColor (SquareEvent address)

and let routeSP compute the concrete addresses of the neighbours. This perhaps makes the communication pattern more visible in the program text and prevents errors in the implementation of atomsSquareF from breaking the pattern.

Since the Gadgets system uses indeterministic process scheduling, it is necessary to explicitly keep track of when an explosion is in progress and when the board is stable, since moves are allowed to be entered only when the board is stable. The implementation of Fudgets is deterministic and internal communication has priority over external communication, so user input is automatically queued until an explosion has subsided.

38.2 The Othello Game

The fudgets version of the game Othello allows a human player to play against the computer or another human player. It was implemented by reusing an existing implementation from 1990 with a TTY-based user interface. 388 of 584 lines were reused without changes. About 100 new lines were added for the new graphical user interface. This demonstrates that the separation of user-interface-specific code and application-specific code is good.

In the implementation of the Explode game, we used a distributed solution: the work of computing the effects of the users' moves is handled almost entirely by the square fudgets. In the implementation of Othello, we have taken the opposite approach: the board fudget only displays the board and receives user input. The checking of the validity of a move and computation of its effect is handled by a stream processor attached in the typical way with the loopThroughRightF combinator (see Section 18.2). The structure of the program is:

main = fudlogue (shellF "Othello" ottoF)

ottoF = 
  displayF
  >==< loopThroughRightF (absF newGameSP) ottoBoardF
  >==< buttonF "New Game"

ottoBoardF :: F BoardReq Coord
ottoBoardF = ...

newGameSP = playSP (reptree moves startpos)

playSP :: GameTree -> SP (Either Coord Click) (Either BoardReq String)
playSP current_position = ...

The function reptree (lazily) computes a game tree which has startpos as the root node and where the children of a node are obtained by applying the function moves to it.

The stream processor playSP checks the current position for whose turn it is to play, and then either waits for the user to enter a move or computes a good move for the computer using standard alfa-beta game-tree search.

VI Discussion

39 Efficiency and program transformations

Efficiency considerations are of course important when building software libraries. Below, we discuss some efficiency aspects of stream processors that have attracted our attention while working on the Fudget library.

We can distinguish two kinds of efficiency:

execution efficiency: programs should run reasonably fast.
programmer efficiency: programs should be easy to write.

While execution efficiency was, and to a large extent still is, a weak point of functional language implementations (as compared to C, for example), programmer efficiency is a strong point, and one of the reason why functional languages are interesting in the first place. There is often a trade-off between the two.

In the following section, we will discuss, in the context of the Fudgets system, how we obtain reasonable execution efficiency. We have not tried to quantify programmer efficiency in a way that permits further comparison or judgement.

39.1 Execution efficiency

Two factors that influence how fast fudgets program run are:

the efficiency of the interface to the window system X Windows, in particular efficiency of event processing.
the efficiency of the fudget combinators.

39.1.1 Efficiency of the interface to the window system

The efficiency of the interface to the window system was a concern right from the start of the work on fudgets. The initial implementation used conventional text I/O to talk to a C program which called routines in Xlib and returned the results (see Section 22.3.1). The C program also forwarded events from X to the functional program. This was not a very efficient implementation and hence we tried to minimise the amount of data passed between the window system and the functional program. Although this was done to avoid problems caused by slow execution of functional programs, an additional positive effect is that fudget programs perform well when using a low bandwidth connection (e.g., modem connection) between the X server and the application. Some figures to back up this statement are given in Figure 101. (One can not draw any general conclusions on performance from these, of course.)

Two tiny programs:

The Fudgets counter example from Section 9.4: 13s
The Motif counter example from Figure 112: 14s
Some small programs:

The Fudget calculator from Section 9.8 with 15 buttons: 13s
The Fudgets calculator Cla with 28 buttons: 16s
The calculator xcalc with 40 buttons, from X Windows distribution: 18s
Some larger programs:

The Fudgets WWW browser from Chapter 32: 22s
Mosaic 2.6: 75s
Netscape 3.0: 137s
Netscape 4.04j2: 313s
Figure 101. Comparing the startup times of some programs when running via a 16.8kbps modem connection.

When it comes to event processing, we naturally wanted to to minimise the number of events that has to be handled by the functional program. Fortunately, the X Windows system can do a lot of event processing for the application. By setting event masks and button grabs appropriately, you can often eliminate all insignificant events, i.e., all events that are sent to the application program carry some meaningful information. In simpler window systems, the application has to deal with every little mouse move and button/key presses/releases by itself.

As an example, consider the implementation of a command button. It should behave as follows:

When the pointer is over the area of the screen occupied by the button and the user presses the mouse button, the button image should be changed to look depressed (that is, pressed down, not discouraged!). If the mouse button is released when the button appears depressed, the button command is triggered.
If the mouse pointer leaves the button image, it should revert to its normal (raised) appearance (indicating that nothing will happen if the user now releases the mouse button). If the user returns the pointer to the button image, without releasing the mouse button, the button should return to its depressed appearance.

The following type of events are thus of interest to the program:

Mouse button presses (but only if the pointer is within the command button).
Mouse button releases (but only if the mouse button has been pressed while the pointer was inside the command button).
Mouse motion (but only if the mouse button has been pressed while the pointer was inside the command button and only if the pointer crosses the border of the screen area occupied by the command button).

In the X windows system a button grab, (see XGrabButton() in the Xlib manual) with an event mask that selects button presses/releases and enter/leave window events (each GUI element is a window), can be used to select exactly these events, with only one small exception: if the mouse pointer enters the button area, the mouse button is pressed, the pointer leaves the button area and the mouse button is released, the program will receive an insignificant button release event. The important thing is that no unnecessary motion events will be received.

39.1.2 Efficiency of the Fudget combinators

39.1.2.1 Efficiency of different representations of stream processors

Two of the stream-processor representations presented above have been used in practice. Early versions of the Fudget library used list functions and synthetic oracles (Section 20.4.1). We later changed to the continuation-based representation (Section 20.4.2) since it proved to be slightly more efficient with the compiler we used (HBC [Aug97]).

We also tried a third representation,

data SP i o = StepSP [o] (i->SP i o)

which was slightly less efficient than the continuation-based representation.

In the discussion below, we assume the continuation-based representation (although some of the ideas can be carried over to other representations).

39.1.2.2 Program transformations for efficiency

Using loopThroughRight (Section 18.2) is a general way to adapt an existing stream processor for use in a new context. Another simple and common way to adapt a stream processor is by mapping a function on the elements of the input or output stream:

sp -==- mapSP g
mapSP f -==- sp

For example, tagged parallel composition of fudgets, >+<, can be defined like

fud1 >+< fud2 =
  mapSP post -==- (fud1 -+- fud2) -==- mapSP pre

where pre and post are the appropriate re-tagging functions. However, if implemented directly, such a definition has a rather high overhead.

By transforming >+< to a form not involving -==-, -+- and mapSP, but instead recursion and pattern matching on the stream-processor constructors, a more efficient solution can be obtained.

Programs transformations of this kind are tedious to do by hand, but it could still be worthwhile if the resulting code is to be included in a library. The above described transformation has been done by hand in the Fudget library. We measured the effect on a communication intensive fudget program containing a parallel composition of 50 fudgets (the Space Invaders program described in Chapter 35). The transformation reduced the CPU time consumption by over 35%. Encouraged by this result, we also transformed some more combinators (for example >^=< and >=^< discussed in Section 13.1) in the same way.

It would of course be nicer to have these transformations done automatically, especially when they are needed in application programs. The kind of automatic transformation that would be useful here is deforestation [Wad90], which eliminates intermediate data structures (applications of PutSP and GetSP in this case) by using certain unfold/fold transformations.

39.1.2.3 A practical semi-automatic transformation

Between the manual and fully automatic implementations of the above program transformation is a semi-automatic alternative. It is interesting because it requires less work than the manual solution and it is more likely to be supported by a compiler than the fully automatic solution.

The manual work required in this solution is located in the library. The application programmer need not be aware of it. The automatic work required is inlining (unfold) by the compiler. It actually works even without inlining, but the efficiency gain is not as big.

The expressions we wish to optimise are of the kind illustrated above: a stream-processor combinator applied to mapSP f, for some f. The trick is to make mapSP a constructor in the stream-processor data type:

data SP a b =  PutSP b (SP a b)
            |  GetSP (a -> SP a b)
            |  MapSP (a -> b)
            |  NullSP

Since the type is abstract, adding constructors to it like this will not be visible to application programmers.

Now that MapSP is a constructor, the implementation of serial composition (as shown in Figure 45) can be extended to handle the case when one or both arguments are applications of MapSP in a more efficient way. This means that an expression like

MapSP f -==- MapSP g

can evaluate to

MapSP (f . g)

With inlining, this step can be taken by the compiler and the composition f . g can then be optimised further. Without inlining, we have at least eliminated a use of -==-, and thereby reduced the number of generated applications of the PutSP and GetSP constructors.

We have not tested the above ideas in the Fudget library.

39.1.2.4 Performance measurements

To get some idea of how high the communication overhead is in the fudgets system, we performed some simple measurements.

The first test measures the efficiency of serial composition and compares the operators >==<, >^^=< and -==-. We measured the time it took to send around 5000 messages through a serial composition of a varying number of identity fudgets (or identity stream processors). The program used is shown in Figure 102. It was compiled with HBC and run on a Pentium Pro 200Mhz under NetBSD 1.2 [Neta]. The results are shown in Figure 103. We can see that the time grows roughly linearly with the length of the composition and that serial composition of fudgets is much more expensive than serial composition of stream processors.

The last table in Figure 103 shows the performance of the function composition map id . ... . map id. It is more efficient than the other serial compositions.

import Fudgets

main = fudlogue mainF

mainF = nullF >==< tstF >==< concatSP >^^=< stdinF

tstF = case argReadKey "comb" 1 of
         1 -> nest (idF>==<) idF depth
         2 -> nest (idSP>^^=<) idF depth
         3 -> absF (nest (idSP -==-) idSP depth)

nest f z 0 = z
nest f z n = f (nest f z (n-1))

depth = argReadKey "depth" 0

Figure 102. A program to measure the efficiency of serial composition.

time ./Internal <testinput1 -S -h8M - -depth n
-comb 1 (idF >==< idF >==< ... >==< idF):

n User time GCs GC time Max heap Max stack
0 0.080u 0 0.00
50 4.173u 40 0.10 62432 836
100 8.475u 80 0.25 95840 1410
200 18.418u 163 0.95 159884 3042
400 44.521u 334 3.35 288020 3768
-comb 2 (idSP >^^=< idSP >^^=< ... >^^=< idF):

n User time GCs GC time Max heap Max stack
0 0.100u 0 0.00
50 0.755u 8 0.01 35712 210
100 1.452u 15 0.03 42270 272
200 2.869u 30 0.08 53504 642
400 5.706u 59 0.18 76976 1218
-comb 3 (idSP -==- idSP -==- ... -==- idSP):

n User time GCs GC time Max heap Max stack
0 0.076u 0 0.00
50 0.411u 4 0.01 32524 171
100 0.812u 7 0.00 35840 348
200 1.574u 15 0.04 41956 651
400 3.047u 30 0.07 54924 1260
map id . map id . ... . map id

n User time GCs GC time Max heap Max stack
0 0.000u 0 0.00
50 0.094u 2 0.00 3956 98
100 0.203u 4 0.00 5616 275
200 0.434u 8 0.00 9712 566
400 0.906u 16 0.01 17616 473
Figure 103. The efficiency of serial composition.

The second test measures the efficiency of parallel composition. We measured the time it took to send about 70000 messages through one of the fudgets in a parallel composition of identity fudgets. The program used is shown in Figure 104. The parallel compositions were created by listF,

listF :: (Eq a) => [(a, F b c)] -> F (a, b) (a, c)

which internally constructs a balanced binary tree of parallel compositions and a table for translating the addresses of the fudgets to positions in the tree. The results are shown in Figure 105. The depth of the tree, and hence the time it takes to send a message to a particular fudget in tree grows logarithmically with the size of the parallel composition. However, since all that is known about the address type is that it is an instance of the Eq class, the table lookup has to be implemented as a linear search and hence the lookup time varies linearly with the position in the list. From the results we see that the time of the table lookup soon becomes the dominating factor. This suggests that it would be a good idea to provide alternative combinators to listF, which require the address type to be an instance of the Ord class, or even the Ix class, to reduce the time complexity of the table lookup time to logarithmic or constant, respectively.

import Fudgets

main = fudlogue mainF

mainF = nullF >==< tstF >==< concatSP >^^=< stdinF

tstF = listF [(i,idF) | i<-[1..size]] >=^< (,) sel

size = argReadKey "size" 1
sel = argReadKey "sel" 1

Figure 104. A program to measure the efficiency of parallel composition.

time ./Internal2 <testinput2 - -size n -sel k
k=1

n 2log n time GCs GC time max heap
1 0 1.352u 11 0.02 29908
32 5 2.179u 18 0.03 34924
256 8 2.457u 22 0.07 66744
2048 11 2.989u 27 0.31 317776
n=256

k 2log n time GCs GC time max heap
64 8 4.640u 33 0.11
127 8 7.001u 44 0.12
128 8 6.801u 44 0.16
256 8 11.126u 67 0.24 87880
Figure 105. The efficiency of parallel composition of fudgets.

39.1.3 Space efficiency

A problem that almost inevitably occurs at some point when developing programs in lazy functional languages is space leaks. In early versions of the Fudget library, streams were represented as (potentially infinite) lists. As discussed in Section 20.4.1, this gave us problems with streams being retained indefinitely, eventually causing programs to run out of memory. This problem was first solved by changing the way the compiler (HBC) treats pattern bindings, as described in [Spa93]. Later, the switch to the continuation-based representation of stream processors also eliminated the problem.

40 Comments on Haskell and other language design issues

For the most part, we have found Haskell to be a pleasant language to work with, but there are a small number of features that we are not so pleased with. We discuss them below.

Through experiences with other languages, we have also realised that some languages features not currently supported by Haskell would be useful to have.

40.1 The annoying monomorphism restriction

One of the most annoying features of Haskell, when trying to program in a combinatorial style, is the monomorphism restriction. It means that a definition that is not syntactically a function is not allowed to be overloaded, unless an explicit type signature is provided.

As a simple example, say that you are going to use the function show a lot and want to introduce a shorter name, s say. Because of the monomorphism restriction, you can not write

s = show

There are two solutions: you can provide a type signature

s :: Show a => a -> String
s = show

or you can eta-expand the definition

s x = show x

In the Fudget library, we have used the eta expansion trick whenever possible, since the inclusion of explicit type signatures just entail extra maintenance work when the library is changed. For example, when a type is renamed or a function is made more general, an arbitrary number of type signatures may need to be updated.

Unfortunately, the eta expansion trick can not always be used, because not all overloaded values are functions. For example, fudgets are not functions, so in case you want to introduce a short name for displayF, you have to use a type signature:

dF :: (Graphic a) => F a b
dF = displayF

Even more unfortunately, there are cases when it is not possible to express the type signature. This occurs when the definition is local to another definition which is polymorphic. It can happen that the local type depends on type variables in the outer definition, but Haskell has no mechanism for expressing such types explicitly. Although these cases turn out to be rare in practice, it is a principal flaw of the language.

40.2 The Haskell string + class system anomaly

An inelegance of Haskell is that you can not directly make the type String an instance of a class. This is due to the combination of two facts:

String is not a data type, but a synonym for [Char].
Instance definition can only be made for uninstantiated type constructors, i.e., you can make instances for Char, and for lists in general, but you can not make a particular instance for [Char]. (See [JJM97] for a discussion of class system design choices.)

This has affected the classes Graphic, ColorGen and FontGen presented in Chapter 27, and


    FormElement

in Section 29.2. At one point during the development, we avoided the problem by defining a data type that was used instead of strings,

newtype Name = Name String

but since this required the use of the constructor Name in a lot of places, we later resorted to the same hack that is used for the Haskell classes Show and Read, i.e., we added extra methods for dealing with lists to the classes. This allow the methods for strings to be defined in the instance declarations for Char. This means that instead of getting an instance for String, you get instances for Char, String, [String], [[String]] and so on. For our classes it was not too difficult to invent a meaning for the extra instances: Char was treated as one-character strings. For the Graphic class, (nested) lists of strings are drawn by drawing all the strings using some layout chosen by the layout system. For the ColorGen and FontGen classes, lists were taken to mean spare alternatives: you can write, e.g., ["midnightblue","black"] to provide one nice color and a safe fallback color. Empty lists can give run-time errors, but are also likely to cause typing problems (making the overloading unresolvable) which are discovered at compile time.

40.3 Existentially quantified types

Existentially quantified types [LO92] provide a very nice language feature, in particular in conjunction with Haskell's type classes [Läu94]. We feel that this feature should have been made part the Haskell standard a long time ago. As it is now, existentially quantified types are provided as a language extension by some Haskell compilers (at the time of writing, only HBC [Aug97], as far as we know).

We have found existential types useful in several contexts: the implementation of Gadgets in Fudgets (Chapter 31), the combinators for syntax-oriented manipulation (Chapter 28) and the datatypes for graphics (Chapter 27).

Since existential types are not part of the Haskell standard, we have tried to keep their use away from core machinery of the Fudget library. Instead we use them on the side to provide a nice feature as an additional bonus. This has affected how we used them in the graphics data types. For example, since leaves of drawing usually are of type Gfx, we could have used existential quantification directly in the Drawing type,

data Drawing lbl
  =  Graphic leaf => AtomicD leaf
  |  ...

eliminating the need for the type Gfx. We could also have defined the GCSpec type as

data GCSpec
  =  (ColorGen c, FontGen f) => SoftGC [GCAttributes c f]
  |  HardGC GCtx

allowing you to write for example

SoftGC [GCForeground "red"]

instead of

SoftGC [GCForeground (colorSpec "red")]

40.4 Dependent types

The Fudget library provides two combinators for tagged parallel composition of fudgets: the binary operator >+< and the list combinator listF:

>+< :: F a b -> F c d -> F (Either a c) (Either b d)
listF :: (Eq a) => [(a, F b c)] -> F (a, b) (a, c)

The former allows the composed fudgets to have different types, but composing a large number of fudgets make addressing the individual fudgets clumsy: you use compositions of the constructors Left and Right.

The latter makes it easy to compose many fudgets, but they must all have the same type.

The use of dependent types would allows us to define a combinator that combines the advantages of >+< and listF. In type theory [NPS90], there are two forms of dependent types: dependent products (function types), and dependent sums (pairs). The second form is the one we need here. It allows us to construct pairs, where the type of the second component depends on the value of the first component.

Using a Haskell-like notation, we write

(t::a, b t)

for the pair type where the first component is of type a and the second component is of type b t, where t is the value of the first component. Note that b is a function returning a type.

By viewing t as a tag, we can form lists of tagged values of different type, and define a variant of listF with the following type:

dListF :: Eq a => [(t::a, F (i t) (o t))] -> F (t::a, i t) (t::a, o t)

42 Evaluation and conclusions

In this thesis, we have presented stream processors to support a concurrent programming style in pure functional languages. Stream processors allow programs to be built in a hierarchical structure of concurrent processes with internal state. They thus support modular design of large programs.

With the stream processors defined here, we abstract away from the streams. We define a number of combinators for stream processors, but no operations on the streams themselves. We have considered a number of different implementations of stream processors, some of which are deterministic and work in a pure, sequential functional language without any extensions, and some of which take advantage of parallel evaluation and indeterministic choice (Chapter 20).

We have also presented a library of combinators for constructing applications with graphical user interfaces (Part II) and typed network communication (Chapter 26). Together with a range of applications, the library has demonstrated that the stream-processor/fudget concept is scalable; it can be used to program not only toy examples, but more complex applications, like WWW-browsers (Chapter 32) and syntax-oriented proof editors (Chapter 33). A key combinator here is loopThroughRightSP (Section 18.2), which allows existing stream processors/fudgets to be reused in a style that resembles inheritance in object-oriented programming.

The library also demonstrates that pure functional programming languages are suitable for these tasks, something which was not clear when this work started. Although GUI fudget programs do a fair amount of I/O, response times can be kept sufficiently low (Section 27.5.3).

Since we represent I/O effects by data constructors sent as messages, we have been able to write higher order functions that manipulate I/O effects of fudgets (Chapter 24), which provide a possibility for modifying the behaviour of existing fudgets. A caching mechanism (Section 24.1) and a click-to-type input model (Section 24.2) has been implemented with this method.

The default parameter mechanism (Chapter 15 and 30) demonstrates how Haskell's class system and higher order functions can be combined to simulate a missing language feature. Later, two other GUI libraries, Gadgets (Section 41.3.1) and TkGofer (Section 41.4), have adopted this mechanism.

The fudget graphicsF in Chapter 27 shows that the task of displaying and manipulating graphics can be handled efficiently in a purely functional way. It has been used both in the web browser in Chapter 32, and in the proof editor Alfa in Chapter 33. On top of graphicsF, we have also implemented a set of combinators that allow syntax-oriented editors to be built in a high-level style, resembling combinator parsers (Chapter 28). Our experience with these combinators is limited sofar, but we believe that they can be employed in a future version of Alfa.

Although most stream processors we have shown are programmed in a CPS style, other styles can be used. Simple stream processors can be programmed by using concatMapAccumlSP and a state transition function. A monadic style can also be used, as is demonstrated in Chapter 31.

As the related work shows in Chapter 41, a number of elegant libraries and interfaces have emerged for GUI programming in pure functional languages during the last years. Is it possible to evaluate and compare all these libraries and the Fudget library? This has been done to some extent in the review in [Nob95]. We will not give any further comparison here, but simply point out some distinguishing features of fudgets and stream processors in general:

Stream processors offer a simple concurrency concept which can be implemented in any pure functional language. Of the other toolkits, Concurrent Clean also provides a purely functional process concept, but it has a rather complex implementation [Ach96].
The fudget concept has been implemented on top of a number of GUI toolkits [Nob95][Tay96][RS93][CVM97], something which also gives evidence that fudgets are easy to implement.
Stream processors come with a special programming style. Since no explicit streams, channels, or wires are used, the routing of information between processes must be specified by using combinators. This can be seen as a limitation of the paradigm, and some people indeed find it difficult to adopt. On USENET, this has been formulated as: ``...you could use something like Fudgets to build a GUI, but that's less fun than having teeth pulled'' [O'S96]. An example of the typical amount of routing necessary is shown in the implementation of somF in (Section 28.4, Figure 81), which has a stream processor handling three output and three input streams. An extreme example is the top-level fudget of Alfa (Chapter 33), whose controlling stream processor defines 15 routing functions, to handle five levels deep messages of Either type. By using routing functions defined in one place, adding new subfudgets to the top-level fudget has become a manageable task. It still requires a bit too much of mechanical work and there is a need for some new set of combinators or some other solution to simplify this programming task further.
One could argue that the combinator plumbing of messages imposes a degree of structure on programs which could be healthy. Having explicit identifiers for streams spread over a program results easily in a goto-like spaghetti. The functional language FP by John Backus [Bac78] is entirely based on the use of combinators instead of named variables.
The stream processor concept also offers support the manipulation of migrating processes, with the special feature that when a process is moved, it is completely detached from all streams in its old context (Chapter 25). We are not aware of anything similar in any other toolkit or process calculus. In addition, since stream processors are pure values (in particular, they do not use imperative variables), they can readily be cloned at any time.
As shown in the Chapter 25, the migration mechanism can be applied to fudgets and used to implement drag-and-drop of GUI fudgets.

42.1 Frequently Asked Questions

How important was lazy evaluation in Fudgets library and programming? Could Fudgets be implemented in ML?

When the work on Fudgets started, Haskell used the stream-based I/O model and stream processes were represented as list functions. Nowadays, the continuation-based representation of stream processors is used and Haskell has switched to a monadic I/O system, both of which would work in a strict language. So, lazy evaluation is no longer essential.

A problem with stream-based I/O is the danger of getting ``out of synch'' and reading one result too many or too few. Did this happen to you in practice?

For a while, when we used the list based representation and that representation was visible to the programmer, the programmer had to be aware of the ``fudget law'', that is, the one-to-one correspondence between input and output messages (see Section 20.4.1). We sometimes made mistakes. When the stream processor type was made abstract, the fudget law became built-in and the programmer was relieved from thinking of it. Also, we started doing low level I/O through functions like doStreamIOK (Section 21.4), which effectively removed all problems of this kind.

Haskell has moved from stream-style I/O to monad-style I/O. Your operations are CPS-style, but they could equally be monad style. Did you make that choice consciously? Why?

The monadic programming style had not become popular when we introduced the CPS style combinators, so we did not make a conscious choice between CPS style and monadic style.

Did you come across any situations where Haskell's type system prevented you doing the Right Thing?

Yes. For example, the type XCommand is supposed be an interface to X Windows, but we have added various ``pseudo commands'' that are handled within the Haskell program and never output to the window system. It would have been nice to define the proper commands as a subtype of all commands. Making this distinction in Haskell would require an extra level of tagging, which we felt was not justified. Analogously, the type XEvent contains some ``pseudo events''.

43 Future work

43.1 Towards a calculus for stream processors

Certainly, the implementation of stream processors used in the Fudget library could serve as a semantic base for formal reasoning about stream processor and fudget programs. But we might want to use a more abstract semantics of stream processors, which would also capture truly parallel-evaluating and indeterministic stream processors. Suppose that we have an implementation for indeterministic stream processors. Would the Fudget library still work? Or are we relying on some subtle ordering of messages that today's sequential implementation gives us, thus avoiding tricky race problems? The answer is probably that most of the library would still work, but at some points, we implicitly rely on implementation details. As one example, consider two identity stream processors in parallel:

p :: SP (Either a b) (Either a b)
p = idSP -+- idSP

When using the implementation from the Fudget library, p is nothing but the identity stream processor for type


      Either a b

. But if we were to use indeterministic stream processors, we cannot be sure that message order would be maintained through p. If we first send Left a immediately followed by

Right
      b

to p, why should there be a guarantee that it will output these messages in the same order?

Naturally, the Fudget library does not have a lot of identity stream processors in parallel. Fudgets, on the other side, are abundant in the library, and they very often sit in parallel. One example where implicit assumptions exist about message order output from parallel fudgets is in the radio group fudget radioF. Another, more explicit, assumption was made in the implementation of the Explode game in Section 38.1.1. In Explode, it is crucial that the internal communication after a explosion has priority over external communication. This is what the continuation-based implementation of stream processors gives.

In order to reason formally about indeterministic stream processors, we present the stream-processor calculus (SP-calculus).

43.1.1 Basic stream processors

There are seven basic ways of forming a stream processor. We let the letter x denote a variable, and s, t, ... stream processors.

x (Variable)
s ! t (Put)
x ? s (Get)
s <· t (Feed)
s << t (Serial composition)
s + t (Parallel composition)
l s (Loop)

For the reader who has used stream processors in the Fudget library, these operators should be familiar. The operator ! correspond to putSP, and ? can be seen as a combination of abstraction and getSP: x ? s is the same as getSP (\x -> s). The feed operator in s <· t feeds the message t to the stream processor s (similar to startupSP, which feeds a list of messages to a stream processor). Serial composition corresponds to


        -==-

, and parallel composition and loop are untagged, corresponding to -*- and loopSP.

43.1.2 Congruence rules

Following the style of [BB90], we define a bunch of congruence rules which can be used freely to find reaction rules to apply.

s + t === t + s (Commutativity of +)
(s + t) + u === s + (t + u) (Associativity of +)
(s << t) << u === s << (t << u) (Associativity of <<)
s << (t ! u) === (s <· t) << u (Internal communication in <<)
(s + t) <· u === (s <· u) + (t <· u) (Distributivity of <· over +)
(s ! t) <· u === s ! (t <· u) (Output from <·)
(s ! t) << u === s ! (t << u) (Output from <<)
(x ? s) <· t === s[t/x] (Substitution)

43.1.3 Reaction rules

Whereas the congruence rules in the last section can be freely used in any direction without changing the behaviour of a stream processor, the reaction rules are irreversible, and introduce indeterminism. The reason is that by applying a rule, we make a choice of how message streams should be merged. There are two places where merging occur, in the output from a parallel composition, and in the input to a loop.

(s ! t) + u --> s ! (t + u) ((Output from +))

We can derive a symmetric rule by using the commutativity of +, but when it comes to the loop, we need two rules.

l (s ! t) --> s ! l (t <· s) (Internal input to l)
(l s) <· t --> l (s <· t) (External input to l)

As an example of these rules, consider the stream processor (s ! t) + (u ! v), which can react to s ! (t + (u ! v)), but also to u ! ((s ! t) + v), using commutativity. Similarly, the loop (l (s ! t)) <· u can react to both s ! l (t <· s) <· u and l (s ! t <· u).

43.1.4 The \-calculus embedded

The SP-calculus is more expressive than the \-calculus, and we can define a translation from the \-calculus into the SP-calculus.

[[x]] = x (Variable)
[[\x.M]] = x ? [[M]] (Abstraction)
[[M N]] = [[M]] <· [[N]] (Application)

The substitution rule for the SP-calculus correspond to the beta-rule of \-calculus. However the eta-rule, which would correspond to x ? (s <· x) === s, does not hold in general, something that we will see after having defined equivalence of stream processors.

Having the power of \-calculus, we can define some familiar stream processors, such as the identity stream processor and the null stream processor.

fix = f ? (x ? f <· (x <· x)) <· (x ? f <· (x <· x))
id = fix <· (f ? x ? x ! f)
0 = fix <· (f ? x ? f)

43.1.5 Equivalent stream processors

We can define an equivalence === as the greatest equivalence relation satisfying:

s₁ === s₂ if and only if:

For all o₁ and s'₁ that s₁ can output and become, there must exist an o₂ and s'₂ that s₂ can output and become. Furthermore, o₁ === o₂ and s'₁ === s'₂ must hold.
For all input t, s₁ <· t === s₂ <· t must hold.

From this definition, we can see that x ? (s <· x) === s does not hold if s can output something. The left-hand side is blocked, waiting for input, and could not match the output from s.

43.1.6 Future work

More investigation is needed to turn the SP-calculus into an operational semantics for stream processors:

Check that we have exactly the congruence/reaction rules we need.
Check that the congruence rules form a decidable relation. It must be possible to find all possible reactions in a stream processor.
The equivalence relation is good, but we really want to find a congruence relation.
Relate the SP-calculus to other calculi so that we can reuse their theory.

43.2 Stream processors as Internet agents

The interest in the Internet has resulted in a focus on new features in programming languages. The information exchange over Internet has exploded, and there is a need to exchange not only text, graphics and sound in a smooth way, but programs. For program exchange to be smooth, the receiver of a program must be certain that it does not do nasty things with his computer. This can be achieved by accepting programs in a typed language, where the type should give information about everything that the program can do, including all kinds of side effects and communication. This is a property that stream processors have, they can do nothing but outputting messages in a known type.

There is also an interest in having programs running for a while at one site, then moving on to other sites, while gathering information etc. Such programs are often called mobile agents. As we have seen in Chapter 25, the necessary machinery for mobile agent programming is already there in the stream-processor concept. However, we need support in the underlying language implementation so that values that are closures can be exchanged between computers.

`>==< :: F a b -> F c a -> F c b`	`-- serial composition`
`>*< :: F a b -> F a b -> F a b`	`-- parallel composition`
`loopF :: F a a -> F a a`	`-- loop`

`Process`	Gadget processes with state
`Process0`	Processes without state
`SPms`	Stream-processor state monads
`SP`	Plain stream processors

x	(Variable)
s ! t	(Put)
x ? s	(Get)
s <· t	(Feed)
s << t	(Serial composition)
s `+` t	(Parallel composition)
l s	(Loop)

s `+` t	===	t `+` s	(Commutativity of `+`)
(s `+` t) `+` u	===	s `+` (t `+` u)	(Associativity of `+`)
(s << t) << u	===	s << (t << u)	(Associativity of <<)
s << (t ! u)	===	(s <· t) << u	(Internal communication in <<)
(s `+` t) <· u	===	(s <· u) `+` (t <· u)	(Distributivity of <· over `+`)
(s ! t) <· u	===	s ! (t <· u)	(Output from <·)
(s ! t) << u	===	s ! (t << u)	(Output from <<)
(x ? s) <· t	===	s[t/x]	(Substitution)

l (s ! t)	-->	s ! l (t <· s)	(Internal input to l)
(l s) <· t	-->	l (s <· t)	(External input to l)

[[x]]	=	x	(Variable)
[[\x.M]]	=	x ? [[M]]	(Abstraction)
[[M N]]	=	[[M]] <· [[N]]	(Application)

fix	=	f ? (x ? f <· (x <· x)) <· (x ? f <· (x <· x))
id	=	fix <· (f ? x ? x ! f)
0	=	fix <· (f ? x ? f)

Table of Contents