The simplest combinator is the one for serial composition,
(-==-) :: SP b c -> SP a b -> SP a c
It connects the output stream of one stream processor to the
input stream of another, as illustrated in
Figure 29. Streams flow from right to left, just like
values in function compositions,
f . g.
Figure 29. Serial composition of stream processors.
Serial composition of stream processors is very close to
function composition. For example, it obeys the following law:
mapSP f -==- mapSP g = mapSP (f . g)
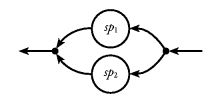
The combinator for parallel composition in
Figure 30 is
indeed the key combinator for stream processors. It allows us
to write reactive programs composed by more or less
independent, parallel processes. The output streams should be
merged in chronological order. We will not be able to achieve
exactly this in a functional language, but for stream
processors whose behaviour is dominated by I/O operations
rather than internal computations, we will get close enough for
practical purposes.
Figure 30. Parallel composition of stream processors.
There is however, more than one possible definition of parallel
composition. How should values in the input stream be
distributed to the two stream processors? How should the
output streams be merged? We define two versions:
- Let
sp1 -*- sp2 denote parallel composition where input
values are propagated to both sp1 and sp2, and output is
merged in chronological order. We will call this version
untagged, or broadcasting parallel composition. - Let
sp1 -+- sp2 denote parallel composition where the
values of the input and output streams are elements of a
disjoint union. Values in the input stream tagged Left or
Right are untagged and sent to either sp1 or sp2,
respectively. Likewise, the tag of a value in the output
stream indicates which component it came from. We will call
this version tagged parallel composition.
The types of the two combinators are:
(-*-) :: SP i o -> SP i o -> SP i o
(-+-) :: SP i1 o1 -> SP i2 o2 -> SP (Either i1 i2) (Either o1 o2)
Note that only one of these needs to be considered as
primitive. The other can be defined in terms of the
primitive one, with the help of serial composition and some
simple stream processors like
mapSP and
filterSP.
- Example:
- Define
-*- in terms of -+-, and vice
versa. - Solution:
(-*-) :: SP i o -> SP i o -> SP i o
sp1 -*- sp2 =
mapSP stripEither -==-
(sp1 -+- sp2) -==-
toBothSP
stripEither :: Either a a -> a
stripEither (Left a) = a
stripEither (Right a) = a
toBothSP :: SP a (Either a a)
toBothSP = concatMapSP (\x -> [Left x, Right x])
(-+-) :: SP i1 o1 -> SP i2 o2 -> SP (Either i1 i2) (Either o1 o2)
sp1 -+- sp2 = sp1' -*- sp2'
where
sp1' = mapSP Left -==- sp1 -==- filterLeftSP
sp2' = mapSP Right -==- sp2 -==- filterRightSP
filterLeftSP = mapFilterSP stripLeft
filterRightSP = mapFilterSP stripRight
stripLeft :: Either a b -> Maybe a
stripLeft (Left x) = Just x
stripLeft (Right _) = Nothing
stripRight :: Either a b -> Maybe b
stripRight (Left _) = Nothing
stripRight (Right y) = Just y
Serial composition creates a unidirectional communication
channel between two stream processors. Parallel composition
splits and merges streams but does not allow the composed
stream processors to exchange information. So, with these
two operators we cannot obtain bidirectional communication
between stream processors. Therefore, we introduce
combinators that construct loops.
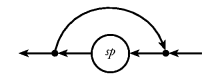
The simplest possible loop combinator connects the
output of a stream processor to its input, as illustrated in
Figure 31. As with parallel composition, we define two
versions of the loop combinator:
Figure 31. A simple loop constructor.
loopSP sp, - output from sp is both
looped to the input of sp and propagated to the
output, outside the loop.
loopLeftSP sp, - output from sp is required to be in
a disjoint union. Values tagged
Left are looped and values
tagged Right are output. At the input, values from the
loop are tagged Left and values from the outside are
tagged Right.
The types of these combinators are:
loopSP :: SP a a -> SP a a
loopLeftSP :: SP (Either l i) (Either l o) -> SP i o
Each of the two loop combinators can be defined in terms of
the other, so only one of them needs to be considered
primitive.
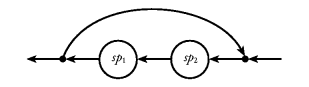
Using one of the loop combinators, one can now obtain
bidirectional communication between two stream processors as
shown in Figure 32.
Figure 32. Using a loop to obtain bidirectional communication.
Another example shows that we can use loops and parallel
composition to create fully connected networks of stream
processors. With an expression like
loopSP (sp1 -*- sp2 -*- ... -*- spn)
we get a broadcasting network. By replacing
-*- with
-+- and some tagging/untagging, we get a network with
point-to-point communication.
- Example:
- Define
loopSP in terms of loopLeftSP and vice versa. - Solution:
- Defining
loopSP in terms of loopLeftSP is
relatively easy:
loopSP :: SP a a -> SP a a
loopSP sp =
loopLeftSP
(toBothSP -==- sp -==- mapSP stripEither)
Vice versa is a bit trickier:
loopLeftSP :: SP (Either l i) (Either l o) -> SP i o
loopLeftSP sp =
mapFilterSP post -==-
loopSP sp' -==-
mapSP Right
where
post (Left (Right x)) = Just x
post _ = Nothing
sp' = mapSP Left -==- sp -==- mapFilterSP pre
where
pre (Right x) = Just (Right x)
pre (Left (Left x)) = Just (Left x)
pre _ = Nothing