Alfa

Natural Deduction Style Proofs

Alfa allows proofs to be presented in natural deduction style. In particular, Alfa provides library modules that defines connectives, quantifiers and proof rules for propositional logic and predicate logic. Using these, Alfa can be (and has been) used as tool for teaching basic logic, since the user can construct proofs without first learning all about the logical framework (type theory).

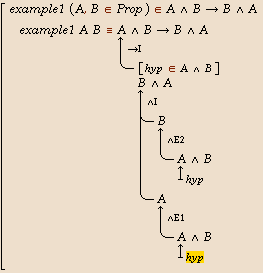
Below, we describe how to construct a proof that logical conjunction is commutative, as illustrated by the following animation. Apart from the first two steps, each step in the animation corresponds to one mouse click or one key press.

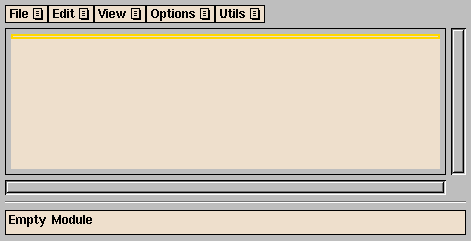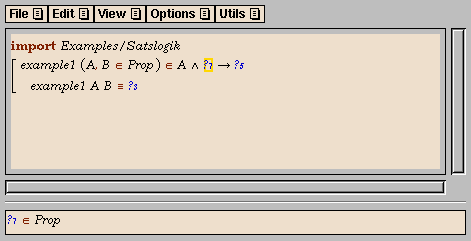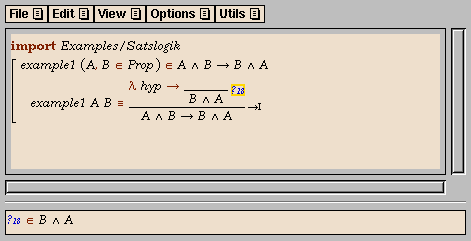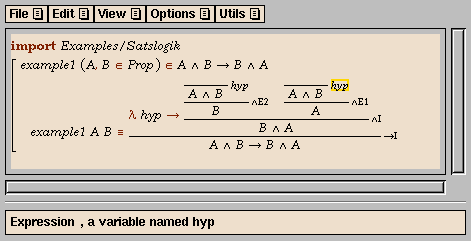
Building a proof

Here are the necessary steps.

Preparations

Import the logic you want to use, in this case Examples/Satslogik for (constructive) propositional logic. Use the Import... command from the File menu, click on the Library button, then on the Examples directory, then on Satslogik.
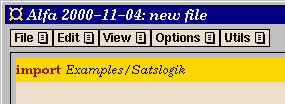
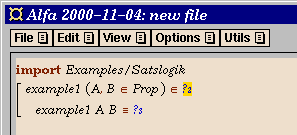
Add a new definition (e.g., by using the command New Declaration in the Edit menu). Here you give the new proof a name, and introduce the propositional variables that occur in the proposition. 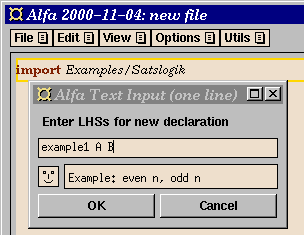After pressing the OK button (or the Return key), we have the following skeleton definition:
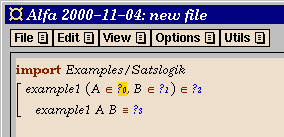
Fill in the type of the propositional variables, which should be Prop, by clicking on Prop in the menu window.
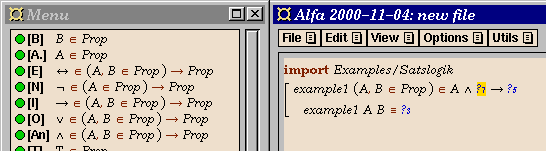
Enter the propsition. You can build it in a top-down order by clicking on the appropriate connectives and propositional variables in the menu window.
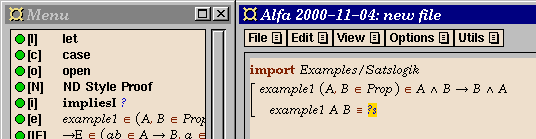
The last thing to do before we can start working on the proof, to make the proof appear in natural deduction style, you have to use the command ND Style Proof from the menu.

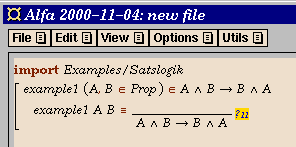
We are now ready to start working on the proof.

To simplify things for students, teachears can prepare exercise files where these steps have already been performed.

Working on the proof

Once the preparations are done, you can concentrate on what proof rules to use to construct the proof. The proof is built top-down, i.e., you start from the final goal and work towards simpler propositions that can be proved directly from assumptions or axioms (i.e., proof rules without any premises). All you have to do is put the cursor on a question mark (?) beside a proof rule and fill in what rule to use by clicking on the name of a suitable rule in the menu window.

In our example, the proposition to be proved is an implication, so a natural first step is an implication introduction, which we can click on in the menu to obtain the following:

When the proof is complete, you might want to save it by using the command Save or Save As... in the File menu.

Useful things to know

If you in the Options menu select the alternative Filter through type checker, only applicable proof rules will be shown in the menu.
Elimination rules are always applicable, since the allow you to conclude anything. This doesn't meen that using them is always appropriate.
After using an elimination rule, the new subgoals usually contains some metavariables (?). Most of the time, there is no need to fill in these manually, just go ahead and fill in the next proof rule to use intead.
Assumptions are referred to by names that are shown with a lambda to the left of the rule where the assumption is discharged. To find out what is assumed click on the name of the assumption next to the lambda.
You can use Undo to go back one or more steps if you used the wrong proof rules.
You can mark and delete arbitrary parts of your proof, but, you may then need to use the menu command ND Style Proof again, to make the new proof appear in natural deduction style.
Proofs presented in Natural Deduction style easily become rather wide. Top-Down Proof Tree is an alternative proof presentation style that can be selected in the View menu. See below.

Defining your own proof rules

You can easily define your own proof rules, since they are just functions. When a function is used as a proof rule in a natural deduction style proof, all visible arguments are assumed to be subproofs, so arguments that aren't subproofs should probably be hidden. For example, to use the commutativity of conjuction above as a proof rule, we would first hide the two first arguments (the propositional variables). See the section User defined layout in the user's guide for how to do this.

A larger example

As a larger example, here is part of a proof of the correctness of insertion sort. This example also illustrates that you can mix natural deduction style with other constructions in the logical framework, such as local definitions.

Alternative proof presentation styles

Proofs presented in Natural Deduction style can easily become rather wide, particularly when propositions contain large terms. An alternative proof style is Top-Down Proof Tree, which can be selected from the View menu. As an example of this proof style, below is the above proof that conjunction is commutative: