Alfa - User's Guide

Alfa is a WYSIWYG proof editor. It allows you to, interactively and incrementally, define theories (axioms and inference rules), formulate theorems and construct proofs of the theorems. All steps in the proof construction are immediately checked by the system and no erroneous proofs can be constructed. The logical framework used is Agda, implemented by Catarina Coquand, based on work by Thierry Coquand. It is a version of Per Martin-Löf's Type Theory.

Alternatively, you can view Alfa as a syntax-directed editor for a small purely functional programming language with a type system that provides dependent types. In fact, the functional language is very similar to the language Cayenne by Lennart Augustsson.

This document describes how to use the WYSIWYG editor, but it does not explain Type Theory.

Before you start playing with Alfa, please note that Alfa is currently under development and that you are using a test version only. Beware that Alfa

• does not warn you about destructive operations, like quitting without saving or overwriting existing files. (Destructive editing operations can be undone and redone using the undo/redo history.)
• has some bugs,
• dies without warning if it runs out of memory. Use a large heap and save your work often!
• is work in progress. Things don't always work exactly as stated in this user guide!

Fore more details, see Limitations of the current version.

Alfa is started with the command

alfa [ rtflags ] [ - flags ]

where

rtflags

is an optional list of flags for the Haskell run-time system. A useful flag is -HheapsizeM, which sets the heap size to heapsize megabytes. The default is 30 (25 in older versions), which is enough for editing small documents. A 30MB heap is too big if you run Alfa on a computer with 32MB of RAM or less.

flags

is an optional list of flags interpreted by Alfa. For details, see Command line syntax. Notice the single - preceding these flags.

Alfa can be stopped by selecting the Quit command from the File menu.

When Alfa is started it opens two windows:

• the main editing window showing the document being edited. The editing window also has a number of menus: File, Edit, View, Options and a Utils menu. (See also the separate document Overview of the menus for explanations of the commands in these menus.) At the bottom of the window there is a display, which shows information relating to the currently selected part of the document, e.g., the type of a place holder.
• the menu window, which shows a context sensitive menu of editing operations, guiding the user in the proof process. The commands in the menu may be preceeded by a status inicator, which is green when the command is applicable and red otherwise.

Closing the main editing window is the same as quitting Alfa. Closing the menu window causes it to disappear, but you can get it back with a command in the Utils menu.

The size of the info display at the bottom of the main editing window is adjusted automatically to fit the currently displayed message, but you can also resize it manually by dragging the separating line.

The commands shown in the various menus can be executed by selecting them using the mouse, but most of them also have keyboard shortcuts that can be used instead.

• The commands shown in the menu window have keyboard shortcuts that are displayed in square brackets [ ]. They are one or more keys long and should be entered without pressing a modifier key like Meta or Control.

• The commands shown in the other menus have shortcuts that are displayed with a preceeding diamond . They are exactly one key long and should be entered with the Meta key pressed. (The Meta key is marked with a diamond symbol on some Sun keyboards and with the text Alt on many other keyboards.)

Alfa allows you to edit a document, which is a sequence of declarations. A declaration is a group of (possibly) mutually recursive definitions. A definition associates a name with a type and a value of that type (x = a : A). (The syntax and meaning of expressions follow Agda's definitions and is not covered in this document.) The names introduced in a declaration are in scope in that declaration and following declarations.

The two most common editing operations are probably adding declarations and filling in place holders (instantiating meta variables). The former is explained below. The latter can be done in many ways, as noted on the quick reference page Top 10 ways to fill in a place holder.

You can add a new declaration to the end of the document by selecting the command New Declaration from the Edit menu in the editing window. You will then have to enter the names to be defined in the declaration in a pop-up window. The names should be separated by commas. You can also include the names of formal parameters in the list.

You can also add declarations in arbitrary places in the document by clicking in the empty space just above or below an existing declaration and then selecting the command Insert New Declaration in the menu window and proceeding as above. (Note: this way of adding declaration is less efficient since is not directly supported in the proof engine and requires the entire module to be rechecked.)

Provided the names defined in a declaration are not in use, the declaration can be deleted by selecting it and executing the Delete operation (which is shown in menu window). You can actually delete a declaration, even if the names are in use. Affected declaration will then be marked with an error bar.

Most editing is done by selecting a part of the document, usually a place holder, declaration or expression, and performing an editing operation on it. Applicable editing operations are displayed in the menu window. They can be executed by clicking on them or by typing the key combination shown in square brackets. (Note: the keyboard shortcuts are generated dynamically, so the same alternative may be assigned different keys in different contexts.) Further editing operations are provided in the Edit menu.

Note: some of the commands in the Edit menu may not be applicable, but there is no visual feedback for this in the current version.

By clicking at some point in the editing window you select the smallest syntactic unit containing that point. You can also use the following keys:

• Space: selects the next (or the first) place holder. With Shift it selects the previous (or the last) place holder.
• Up: selects the parent of the currently selected node in the syntax tree.
• Down: selects the first (leftmost) child of the currently selected node.
• Left/Right: selects the smallest selectable unit to the left/right of the current node.
• Meta-Left/Right: selects the left/right sibling of the current node, e.g., the previous/next item in a sequence.

Cut-and-Paste editing works in much the same way as in other programs.

The currently selected part of the document can be copied to the (invisible) clipboard by executing the Copy command in the Edit menu. It can then be pasted in other places in the document. It can also be pasted in other X Windows programs, e.g., emacs, usually by pressing the middle mouse button (in emacs you can also use C-y). When a place holder is selected and the clipboard contains an expression of a suitable type, the place holder can be replaced with the expression by executing the Paste command in the Edit menu. A syntax error may occur if the clipboard contains some text (from a text editor) that does not form a syntactically correct expression.

You can paste a declaration when the empty space immediately above or below a declaration is selected and the clipboard contains a declaration.

You can also paste on top of existing expressions and declarations. If a type error occurs, you get an error bar.

You add new constructors to an existing data type by selecting the data expression and picking the command Add constructor from the menu window. After this, you probably also need to add branches for the new constructors in some case expressions. This is done in the same way, i.e., select the case expression and pick the command Add branch from the menu window.

The type checker may not accept case expression that aren't exhaustive, so adding a constructor to a data type may give rise to an error, causing declarations containing affected case expressions to be marked with an error bar. It is still possible to add a branch for the new constructor.

It is also possible to delete branches from case expressions and constructors from data types. To do this, select the branch or constructor and pick the Delete command from the menu window (or the Edit menu). Deleting a constructor that is still in use somewhere will cause affected declarations to be marked as erroneous.

In some situations, e.g., when using the Give command and when constructing case expressions, you have to enter expressions as text. The syntax to use in these cases is the same syntax Alfa uses for storing documents in files. (See the documentaton of Agda for details.) This means for example that constructors should be suffixed with @_ and that you can not leave out hidden arguments. You can use place holders (? or {| |}) for subexpressions you don't want to fill in.

Alfa currently provides the following ways for the user to influence the layout:

• Options for individual identifiers: the number of hidden arguments, infix precedence and associativity, quanifier notation, etc. These options applies to every occurence of an identifier.
• Some global settings: enable/disable argument hiding, enable/disable compact notation, proof style, etc.

About Argument hiding

Terms in the monomorphic type theory often contain a lot of redundant type information. This type information is often inferred by the proof engine and does not have to be filled in by the user. The argument hiding mechanism is provided as a way of hiding some redundant information and thereby making the terms smaller and more readable.

You can set the number of hidden arguments for an identifer as described below. In expressions where an identifier with n hidden arguments is applied to some arguments, the first n arguments will be invisible. (In earlier versions of Alfa, they were represented by a °, allowing you to see that there was something hidden.)

Note that argument hiding is a lexical property of an identifier and is not connected to the scope of a certain binding.

The View menu contains commands for switching on and off the argument hiding mechanism.

As an example of the effect of argument hiding, consider the definition of the list function map:

Without argument hiding	With 2 hidden arguments

The layout options for an identifier can be edited by clicking on a binding occurence of the identifier and choosing the command Change layout options shown in the menu window. This pops up a window where you can change the various options.

The layout options show in this window, from top to bottom are:

Number of hidden arguments

Enter a number here to set the number of hidden arguments.

Display As

If present, the string entered in this field will be shown instead of the real name of the identifier. This string can be any combination of characters, not just legal identifiers, and it does not affect the abbreviations shown in the menu window.

Use Symbol Font

The identifier will be displayed using the symbol font instead of the ordinary font.

Use Image File

The string entered in the Display As: field is interpreted as the name of a file containing an image in the xbitmap format to show intstead of the real name.

Nonfix/Infix/Postfix

This affects how an application of the identifier to some arguments are displayed:

Nonfix	Infix	Postfix
op	op	op
op x	(x op)	x op
op x y	x op y	(x op) y
op x y z	(x op y) z	(x op) y z

Infix ternary/Infix 4ary

These options are like Infix but arguments are also put above and/or below the operator.

Quantifier

This option switches on quantifier notation. A quantifiers is a function that normally is applied to a lambda abstraction. For example, the application Forall (\(x::A)->B x), could appear as . The domain of quantification can be shown, as in this example, or be hidden.

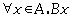
Big Operator

This option causes applications of the form f a b c to be displayed as

b
f	c
a

and applications of the form f a b (\ i -> c) to be displayed as

b
f	c
i=a

Tuple

This options shows the arguments of the function in angle brackets, separated by commas. The name of the function will not be visible.

Fraction

For functions applied to two arguments, this option displays the argument vertically, separated by a horizontal line. The name of the function will not be visible.

Mixfix operator

This option allows you to interleave arguments and arbitrary strings. The arguments will be inserted in place of _ characters in the name of the function (or the Display As string, if given). For example, the application

if_then_else_ x y z

would be displayed as

if x then y else z

It is also possible to use digits to refer to arguments at specific positions. For example, by changing the Display As string for the above function to

2 if 1, 3 otherwise

the same application would be displayed as

y if x, z otherwise

Associativity and precedence

This affects where parentheses are insterted when expressions contain nested applications of infix/mixfix/distfix operators.

The View menu contains commands for switching on and off compact notation. In the current version, compact notation means that function types and lambda expressions are abbreviated:

Full notation	Compact notation
(a:A) -> (b:B) -> C	(a:A,b:B) -> C
(a:A) -> (b:A) -> C	(a,b:A) -> C
\ x -> \ y -> e	\ x y -> e

It also causes nested case expressions to be displayed in a more compact way. Definitions where the right hand side is a case expression is displayed in an equational style. Nested case expressions are displayed as nested patterns.

Example:

Normal	Compact

Bug warning: some editing operations don't work properly when compact notation is in use, so you might want to turn it off temporarily. For example, if you change (a,b:A)->C to (a,b:B)->C you will see (a,b:B)->C, but you will get (a:B,b:A)->C.

Provided they are constructed in a certain way, proofs can be presented in natural deduction style, and other similar styles. See the separate tutorial on Natural Deduction Style Proofs for further details.

The command Evaluate Expressions in the Utils menu pops up a window where you can enter expressions to be evaluated. The expressions have to entered as text (as explained above). When a place holder is selected, the expressions will be evaluated in the context of that place holder. Otherwise they will be evaluated in the top level context (i.e., all identifiers defined on the top level are in scope).

Note: there is a termination test, so if you try to evaluate an expression that doesn't terminate, or one that requires too many computation steps, you will get an error message.

The arrow buttons in this window allow you to step back and forth in the evaluation (the < and > buttons) or go directly to the original form and the normal form of the expression (the << and >> buttons).

Since Alfa is a syntax directed editor, it is not possible to construct syntactically incorrect documents. However, text representing expressions or other syntactic entities can of course contain errors and can enter the system in the following ways:

• When opening a file. If there is a syntax error in a file, Alfa displays an error message indicating the line and column where the error occurred, and refuses to open the file. This can normally only happen if the file has been created or modified with some editor other than Alfa.
• When entering expressions as text. In this case, Alfa moves the cursor to the error position, displays a sad smiley and an error message, and refuses to accept the expression.
• When pasting. When you have selected some text in another editor and try to paste it into Alfa, you will get an error message if the text does not represent an expression, declaration or whatever syntactic entity is required where you try to paste it.

Everything entered into Alfa is immediately type checked, so it is usually impossible to create type incorrect documents. However, there are some cases when editing operations that lead to type errors are allowed:

• When opening a file. If a file contains a type incorrect declaration, the file is still opened, but the declaration containing the error is marked with an error bar. Declarations following the erroneous one are left unchecked and marked with an error bar too.
• Operations that aren't directly supported by the proof engine, (currently most editing operations except instantiating a place holder) are handled by rechecking the entire document. This can result in declarations becoming erroneous and marked with an error bar, as when an erroneous file is opened.

The error bar is a red vertical bar to the left of a declaration. It indicates that the type checking of the declaration (or some declaration preceeding it) has failed and that it has been left in an unchecked state.

When a declaration is in the unchecked state, only limited editing operations are available inside it. In particular, you can not see the type of place holders, and things you fill in aren't type checked. After making some changes, you can use the command Check Again to have the type checker re-check the declaration and, if the error has been corrected, return it to the normal, type checked state.