As we have seen above, the most natural representation of
streams, i.e., as lists, requires parallel evaluation and
indeterministic choices. But there are solutions that allow
you to stay within a purely functional language, like
Haskell. Although they do not provide the same degree of
parallelism, they have proved to be adequate for practical
use. The solutions below have been used in the implementation of
the Fudget system.
As seen in
Section 20.2, the problem with the most natural
representation of stream processors--representing
streams as lazy lists and stream processors as functions on
lazy lists--is the implementation of parallel composition. It
is impossible to know in which order the output streams should
be merged.
If we impose the restriction that sp1 and sp2 must produce
output at the same rate, then sp1 -*- sp2 can
be defined as:
(sp1 -*- sp2) xs = merge (sp1 xs) (sp2 xs)
where merge (y:ys) (z:zs) = y:z:merge ys zs
However, it is awkward to impose such a constraint between the output
streams of two different stream processors. Also, this
solution does not work well for tagged parallel composition. A
more useful constraint relates the input and output stream of
a single stream processor.
- We impose the constraint that there must be a one-to-one
correspondence between elements in the output and the input
stream, i.e., a stream processor must put one element in the
output stream for every element consumed from the input
stream.
The function
map is an example that satisfies this
constraint, whereas
filter is a function that does not.
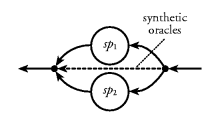
With this restriction, tagged parallel composition can easily
be implemented: the next element in the output stream should
be taken from the stream processor that last received an
element from the input stream. The following implementation of
tagged parallel composition uses this fact by merging the
output streams using a stream of synthetic oracles computed
from the input stream (see also Figure 43):
(-+-) :: SP a1 b1 -> SP a2 b2 -> SP (Either a1 a2) (Either b1 b2)
(sp1 -+- sp2) xs = merge os (sp1 xs1) (sp2 xs2)
where
xs1 = [ x | Left x <- xs ]
xs2 = [ y | Right y <- xs ]
-- os : a synthetic oracle stream
os = map isLeft xs
merge (True:os) (y:ys) zs =
Left y:merge os ys zs
merge (False:os) ys (z:zs) =
Right z:merge os ys zs
isLeft (Left _) = True
isLeft (Right _) = False
Figure 43. Parallel composition of stream processors using synthetic oracles.
This solution has some practical problems, however. As it
stands above, there is a potentially serious space-leak
problem. Consider the evaluation of an expression like
(sp1 -+- sp2) [Left n | n<-[1..]]
Here,
sp2 will never receive any input. This means that
merge will never need to evaluate the argument
(sp2 xs2), which holds a reference to the beginning of the
input stream via
xs2. This would cause all input
consumed by the composition to be retained in the
heap. However, provided that pattern bindings are implemented
properly [
Spa93], this problem can be solved by computing
xs1 and
xs2 with a single recursive definition that
returns a pair of lists:
split :: [Either a b] -> ([a],[b])
split [] = ([],[])
split (x:xs) =
case x of
Left x1 -> (x1:xs1,xs2)
Right x2 -> (xs1,x2:xs2)
where
(xs1,xs2) = split xs
Another problem is that the 1-1 restriction is rather severe.
What should a stream processor do if it does not want to put a
value in the output stream after consuming an input (like
filter)? What if it wants to output more than one value?
Obviously, if an implementation with this restriction is given
to a programmer, he will invent various ways to get around
it. It is better to provide a solution from the
beginning.
One way to relieve the restriction is to change the
representation of stream processors to
type SP a b = [a] -> [[b]]
thus allowing a stream processor to output a list of values to
put in the output stream for every element in the input
stream. Unfortunately, with this representation the standard
list functions, like
map and
filter, can no
longer be used in such a direct way. For example, instead of
map f one must use
map (\x->[f x]). Serial
composition is no longer just function composition, rather it
is something more complicated and less efficient. Also, it is
still possible to write stream processors that do not obey the
1-1 restriction, leading to errors that can not be detected by
a compiler. Consequently, it is not a good idea to reveal this
representation to the application programmer, but rather
provide the stream-processor type as an abstract type. And
while we are using an abstract type, we might as well use a
better representation.
Instead of using lists, the Fudget library uses a data
type with constructors corresponding to the actions a stream
processor can take (as described in Section 3.2):
data SP i o
= NullSP
| PutSP o (SP i o)
| GetSP (i -> SP i o)
We call this the
continuation-based representation of
stream processors. The type has one constructor for each
operation a stream processor can perform. The constructors
have arguments that are part of the operations (the value to
output in
PutSP), and arguments that determine how the
stream processor continues after the operation has been
performed.
The continuation-based representation avoids the problem with
parallel composition that we ran into when using the
list-based representation, since it makes the consumption of
the input stream observable. With list functions, a stream
processor is applied to the entire input stream once and for
all. The rate at which elements are consumed in this list is
not observable from the outside. With the continuation-based
representation, a stream processor must evaluate to GetSP
sp
each time it wants to read a value from the input stream. This
is what we need to be able to merge the output stream in the
right order in the definition of parallel composition.
An implementation of broadcasting parallel composition is
shown in Figure 44. The implementation of tagged parallel
composition is analogous. Note that we arbitrarily choose to
inspect the left argument sp1 first. This means that even if
sp2 could compute and output a value much faster than
sp1, it will not get the chance to do so.
NullSP -*- sp2 = sp2
sp1 -*- NullSP = sp1
PutSP o sp1' -*- sp2 = PutSP o (sp1' -*- sp2)
sp1 -*- PutSP o sp2' = PutSP o (sp1 -*- sp2')
GetSP xsp1 -*- GetSP xsp2 = GetSP (\i -> xsp1 i -*- xsp2 i) |
Figure 44. Implementation of parallel composition with
the continuation-based representation.
With the continuation-based representation, serial
composition can be implemented as shown in Figure 45.
NullSP -==- sp2 = NullSP
PutSP o sp1' -==- sp2 = PutSP o (sp1' -==- sp2)
GetSP xsp1 -==- NullSP = NullSP
GetSP xsp1 -==- PutSP m sp2' = xsp1 m -==- sp2'
GetSP xsp1 -==- GetSP xsp2 = GetSP (\i -> GetSP xsp1 -==- xsp2 i) |
Figure 45. Implementation of serial composition with
the continuation-based representation.
A definition of the loop combinator loopSP is shown in
Figure 46.
loopSP sp = loopSP' empty sp
where
loopSP' q NullSP = NullSP
loopSP' q (PutSP o sp') = PutSP o (loopSP' (enter q o) sp')
loopSP' q (GetSP xsp) = case qremove q of
Just (i,q') -> loopSP' q' (xsp i)
Nothing -> GetSP (loopSP . xsp)
-- Fifo queues
data Queue
empty :: Queue a
enter :: Queue a -> a -> Queue a
qremove :: Queue a -> Maybe (a,Queue a)
|
Figure 46. Implementation of loopSP with the
continuation-based representation.
- Example:
- Implement
runSP :: SP a b -> [a] -> [b]. - Solution:
runSP sp xs =
case sp of
PutSP y sp' -> y : runSP sp' xs
GetSP xsp -> case xs of
x : xs' -> runSP (xsp x) xs'
[] -> []
NullSP -> []