9.1 "Hello, world!"

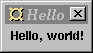
We begin with a simple program that only displays a message in a window. This example illustrates what the main program should look like, as well as some other practical details. As the window dump shows, the window manager adds a title bar to the message.

Here is the source code:

import Fudgets

main = fudlogue (shellF "Hello" (labelF "Hello, world!"))

Note:

• To use the Fudget library, the module Fudgets should be imported.
• A fudget program consists of a number of fudgets combined in a hierarchical structure that makes up one main fudget. The function fudlogue,

  fudlogue :: F a b -> IO ()

  connects the main fudget to Haskell's I/O system, thus starting a dialogue between them. It sets up the communication with the window system, gathers commands sent from all fudgets in the program and sends them to the window system, and distributes events coming from the window system to the appropriate fudgets.
• A fudget program with a graphical user interface needs one or more shell windows (top-level windows). These can be created with the function shellF,

  shellF :: String -> F a b -> F a b

  which given a window title and a fudget, creates a shell window containing the graphical user interface defined by the argument fudget. The fudgets for GUI elements, like labelF, can not be used directly on the top level in a program, but must appear inside a shell window.
• In this simple program, the contents of the shell window are merely a simple string label, that is created with the function labelF,

  labelF :: (Graphic a) => a -> F b c

  The argument is the label to be displayed. The label can be a value of any type that is an instance of the Graphic class. The Fudget library provides instances for many predefined types, including strings. The Graphic class is discussed in Section 27.1.

  Both the input and output types of labelF are type variables that do not occur anywhere else. This indicates that none of the high-level streams are used by labelF.

  labelF has only one parameter: the label to be displayed. Most GUI fudgets come in two versions: a standard version, like labelF, and a customisable version, for example labelF', which allows you to change parameters like fonts and colors, for which the standard version provides default values. See Chapter 15 for more details.

• The size and placement of the GUI elements need not be specified. The fudget system automatically picks a suitable size for the label and the size of the shell is adapted to that.

Useful programs of course contain more than one GUI element. The next example will contain two GUI elements!

9.2 The factorial function

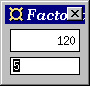
This program illustrates how data is communicated between different parts of a Fudget program. It illustrates a simple way to combine application-specific code (in this case the factorial function) with GUI elements from the Fudget library.

The program shows a numeric entry field at the bottom and a number display at the top. Whenever the user enters a number in the entry field and presses the Return key, the factorial of that number is computed and displayed in the number display.

Here is the source code:

import Fudgets

main = fudlogue (shellF "Factorial" facF)

facF = intDispF >==< mapF fac >==< intInputF

fac 0 = 1
fac n = n * fac (n-1)

Note:

• The program facF is structured as a serial composition of three parts, using the operator >==<. Notice that, as with ordinary function composition, data flows from right to left. The parts are:
  • the numeric entry field intInputF,
  • mapF fac, an abstract fudget (a fudget without a corresponding GUI element) that applies fac, the factorial function, to integers received from the entry field, and
  • the number display intDispF, which displays the computed factorials.
• We have used fudlogue and shellF on the top level as in the previous examples (Section 9.1).

The types of the new library components used in this example are:

>==< :: F a b -> F c a -> F c b
intInputF :: F Int Int
mapF :: (a -> b) -> F a b
intDispF :: F Int a

Although this program does something useful (at least compared to the two previous examples), it could be made more user friendly, e.g., by adding some explanatory text to the user interface. The next example shows how to do this.

9.3 The factorial function, with improved layout

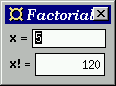
This program shows how to use layout combinators to improve the visual appearance of a Fudget program.

We have made the factorial function example from Section 9.2 more self documenting by adding labels to the entry field and the output display. We have also changed the order of the two parts: the entry field is now above the display.

Here is the source code:

import Fudgets

main = fudlogue (shellF "Factorial" facF)

facF = placerF (revP verticalP) (
        ("x! =" `labLeftOfF` intDispF) >==<
        mapF fac >==<
        ("x =" `labLeftOfF` intInputF))

fac 0 = 1
fac n = n * fac (n-1)

Note:

• We have used the function labLeftOfF to put labels to the left of the entry field and the display. (In Haskell, back quotes can be used to turn any function into an infix operator, as we have done with labLeftOfF here).
• The function placerF can be applied to a composition of fudgets to specify the relative placement of the parts. (The layout system automatically picks some placement if layout is left unspecified.) The first argument to placerF is a placer, in our case revP verticalP, where verticalP causes the parts to be stacked vertically, with the leftmost fudget in the composition at the top, and revP reverses the order of the parts.
• Everything else is as in the previous examples.

The types of the new library components used in this example are:

labLeftOfF :: (Graphic a) => a -> F b c -> F b c
placerF :: Placer -> F a b -> F a b
revP :: Placer -> Placer
verticalP :: Placer

9.4 An up counter

This program illustrates a more general way to combine application-specific code with GUI elements from the Fudget library. It illustrates that state information can be encapsulated. State information is often considered as difficult to handle in pure functional languages; hopefully, this counter example shows how easy it is!

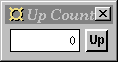
This program has a button and a numeric display. Pressing the button increments the number in the display.

The application-specific code in this example sits between the button and the display. It maintains an internal counter which is incremented and output to the display whenever a click is received from the button.

Here is the source code:

import Fudgets

main = fudlogue (shellF "Up Counter" counterF)

counterF = intDispF >==< mapstateF count 0 >==< buttonF "Up"

count n Click = (n+1,[n+1])

Note:

• As with the factorial example (Section 9.2), the central part of the program (counterF) is a serial composition of three parts. At the output end we see the familiar intDispF. At the input end of the pipe line is a button created with buttonF. It outputs a Click when pressed. The middle component maintains an internal counter. The counter is incremented and output to the display when a Click is received from the button.
• mapstateF, like mapF, allows messages sent between fudgets to be processed in an application-specific way. With mapstateF, an arbitrary number of messages can be output as response to an input message. In addition, the output can depend not only on the current input, but also on an internal state. mapstateF has two arguments: a state transition function and an initial state. When applied to the current state and an input message, the state transition function should produce a new internal state and a list of output messages.

  The function count is the state transition function in this program.

• There is a small pitfall in this program: intDispF automatically displays 0 when the program starts. The initial value of the counter happens to be 0 as well. If the 0 is changed in the definition of counterF, the display will still show 0 when the program starts. One way to fix this is to use the customisable version of intDispF to specify the initial value to display.

The types of the new library components used in this example are:

buttonF :: (Graphic a) => a -> F Click Click
data Click = Click
mapstateF :: (a -> b -> (a, [c])) -> a -> F b c

This and the previous examples show how serial composition creates a communication channel from one fudget to another. But what if a fudget needs input from more than one source? The next example shows one possible solution.

9.5 An up/down counter

This example illustrates how to handle input from more than one source (Figure 6).

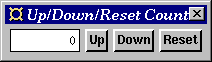
Figure 6. The up/down counter.

The two buttons affect the same counter.

Here is the source code:

import Fudgets

main = fudlogue (shellF "Up/Down Counter" counterF)

counterF = intDispF >==< mapstateF count 0 >==<
           (buttonF filledTriangleUp >+< 
            buttonF filledTriangleDown)

count n (Left Click)   = (n+1,[n+1])
count n (Right Click)  = (n-1,[n-1])

Note:

• The up/down counter is a small extension of the Up Counter (Section 9.4). We have added a button by replacing

  buttonF ...

  with

  (buttonF ... >+< buttonF ...)

  using the operator >+< for parallel composition.
• The output from a parallel composition is the merged output from the two components. Output from the left component is tagged Left and output from the right component is tagged Right. The constructors Left and Right are constructors in the datatype Either.
• The count function will now receive Left Click or Right Click, depending on which button was pressed. It has been adjusted accordingly. (Note that Left Click and Right Click have nothing to do with the left and right mouse buttons!)
• Just to illustrate that buttons can display arbitrary graphics and not just text, we have used two suitable shapes that happen to be provided by the library.
• Everything else is as in the previous example (Section 9.4).

The types of the new library components used in this example are:

>+< :: F a b -> F c d -> F (Either a c) (Either b d)
filledTriangleUp :: FlexibleDrawing
filledTriangleDown :: FlexibleDrawing

9.6 An up/down/reset counter

This example shows how to create parallel compositions of many fudgets of the same type.

This program extends the counter example with yet another button. The counter can now be incremented, decremented and reset.

Here is the source code:

import Fudgets

main = fudlogue (shellF "Up/Down/Reset Counter" counterF)

counterF = intDispF >==< mapstateF count 0 >==< buttonsF

data Buttons = Up | Down | Reset deriving Eq

buttonsF = listF [(Up,     buttonF "Up"     ),
                  (Down,   buttonF "Down"   ),
                  (Reset,  buttonF "Reset"  )]

count n (Up,     Click) = (n+1,  [n+1])
count n (Down,   Click) = (n-1,  [n-1])
count n (Reset,  Click) = (0,    [0])

Note:

• When putting more than two fudgets of the same type in parallel, it is more convenient to use listF than >+<. The argument to listF is a list of pairs of addresses and fudgets. The addresses are used when messages are sent and received from the components in the composition.
• In this program there is a user defined enumeration type Buttons, the elements of which are used as the addresses of the buttons. The messages received by the count function are pairs of Buttons values and Clicks.
• Everything else is as in the previous example (Section 9.5).

The type of the new library component used in this example is:

listF :: (Eq a) => [(a, F b c)] -> F (a, b) (a, c)

9.7 A loadable up/down counter

This example illustrates the use of loops to handle user-interface elements that are used for both input and output (Figure 7).

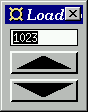
Figure 7. The loadable up/down counter.

The program extends the up/down counter in Section 9.5 by allowing the user to set the counter to any value by entering it in the display field.

Here is the source code:

import Fudgets

main = fudlogue (shellF "Loadable Up/Down Counter" counterF)

counterF = loopThroughRightF (mapstateF count 0) intInputF >==<
           (buttonF filledTriangleUp >+< buttonF filledTriangleDown)

count n (Left n')              = (n',   [])
count n (Right (Left Click))   = (n+1,  [Left (n+1)])
count n (Right (Right Click))  = (n-1,  [Left (n-1)])

Note:

• Instead of intDispF we have used intInputF, which not only displays numbers, but also allows the user to enter numbers.
• We have used the combinator loopThroughRightF to allow the count function to both receive input from and send output to intDispF. In the composition loopThroughRightF fud1 fud2, fud₁ handles the communication with the outside world (the buttons in this example), while fud₂ can communicate only with fud₁, and is in this sense encapsulated by fud₁. In fud₁, messages to/from fud₂ are tagged Left and messages to/from the outside world are tagged Right.

The type of the new library component used in this example is:

loopThroughRightF :: F (Either a b) (Either c d) -> F c a -> F b d

9.8 A simple calculator

As a final example, we show how a slightly larger program, a simple calculcator, can be built using the ideas illustrated by the previous examples (Figure 8).

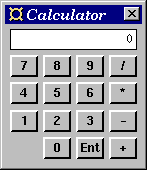
Figure 8. The calculator.

For simplicity, postfix notation is used, i.e., to compute 3+4 you enter 3 Ent 4 +. The source code can be found in Figure 9.

import Fudgets main = fudlogue (shellF "Calculator" calcF) calcF = intDispF >==< mapstateF calc [0] >==< buttonsF data Buttons = Plus | Minus | Times | Div | Enter | Digit Int deriving Eq buttonsF = placerF (matrixP 4) ( listF [d 7, d 8, d 9, op Div, d 4, d 5, d 6, op Times, d 1, d 2, d 3, op Minus, hole, d 0, ent, op Plus]) where d n = (Digit n,buttonF (show n)) ent = op Enter hole = (Enter,holeF) op o = (o,buttonF (opLabel o)) where opLabel Plus = "+" opLabel Minus = "-" opLabel Times = "*" opLabel Div = "/" opLabel Enter = "Ent" calc (n:s) (Digit d,_) = new (n*10+d) s calc s (Enter,_) = (0:s,[]) calc (y:x:s) (Plus,_) = new (x+y) s calc (y:x:s) (Minus,_) = new (x-y) s calc (y:x:s) (Times,_) = new (x*y) s calc (y:x:s) (Div,_) = new (x `div` y) s calc s _ = (s,[]) new n s = (n:s,[n])

Figure 9. Source code for the calculator.

Note:

• The program structure is much the same as in the up/down/reset counter (Section 9.6).
• To specify the placement of the buttons we have used placerF (as in Section 9.3) and the placer matrixP which has the number of columns as an argument.
• The state maintained by the application-specific code (the function calc) is a stack (represented as a list) of numbers. The function calc pushes and pops numbers from the stacks as appropriate. The last clause in the definition means that nothing happens if there are too few values on the stack for an operation.
• As it stands, the calculator can be controlled with the mouse only. The customisable version of buttonF allows you to specify a keyboard shortcut for the button. It would thus be relatively easy to make the calculator controllable from the keyboard.

The type of the new library component used in this example is:

matrixP :: Int -> Placer