In the HCI (Human Computer Interaction) school [
Shn98], it is
good design to first concentrate on a good user interface when
developing a GUI application, then implement the functionality
behind. For example, the
Logical User-Centered Interactive
Design Methodology (LUCID) [
Kre96] consists
of six stages, in which the third stage includes the development
of a so-called key-screen prototype using a rapid prototyping
tool. After a stage of iterative refinement, this prototype is
turned into a full system in the fifth stage.
To promote quick development of prototype programs, a programmer
might prefer to concentrate on the functionality, and ignore the
GUI design (at least to start with). Since this method can make
life easier for the programmer, and to put it in contrast with
HCI, we call it PCI (Programmer Computer Interaction)
oriented.
With the PCI method, the GUI must be generated automatically
somehow. The basic idea is simple, and can be seen as the GUI
variant of the Read and Show classes in Haskell,
which allow values of any type to be converted to and from
strings, using the functions read and show:
read :: Read a => String -> a
show :: Show a => a -> String
Part of the convenience with these classes is that instances can
be derived automatically by the compiler for newly defined
datatypes. By using
read and
show, it is easy to
store data on files, or exchange it over a network (as is done in
Chapter 26).
In this section, we will define the class FormElement,
which plays a similar role to Read and Show, but for
GUIs. Form elements are combined into forms, which can be
regarded as simple graphical editors that allow a fixed number of
values to be edited. They are often used in dialog windows to
modify various parameters in a GUI application.
Assuming that all the necessary instances of FormElement
are available, we show how forms can be generated automatically,
entirely based on the type of the value that the form should
present.
An individual form element displays a value of some type
a. Whenever this value is changed, it will be output by the
element. Such a change occurs when a user enters a new value,
but it should also be possible to change the value from the
program itself.
A candidate type for form elements for a type a is a
fudget with the type a both on input and output.
type FormF t = F t t
The form element class has a method which specifies such a
fudget.
class FormElement t where
form :: FormF t
formList :: FormF [t]
instance (FormElement t) => FormElement [t]
where form = formList
We have used the standard trick of adding a special method
formList which handles lists, so that we can get an
instance for strings (this is discussed in
Section 40.2).
We can now define instances for the basic types integers,
booleans, and strings.
instance FormElement Int
where form = intInputF
instance FormElement Bool
where form = toggleButtonF " "
instance FormElement Char
where formList = stringInputF
We also need instances for structured types. The fundamental
structured types are product and sum.
instance (FormElement t,
FormElement u) =>
FormElement (Either t u)
where form = vBoxF (form >+< form)
instance (FormElement t,
FormElement u) =>
FormElement (t,u)
where form = hBoxF (form >·< form)
Note the vertical layout of alternatives, whereas elements
within an alternative have a horizontal layout.
The combinator >·< puts two fudgets in parallel, just like
>+< and >*<, but input and output are pairs.
(>·<) :: F a1 b1 -> F a2 b2 -> F (a1, a2) (b1, b2)
f >·< g = pairSP >^^=< (f >+< g) >=^^< splitSP
pairSP :: SP (Either a b) (a,b)
pairSP = merge Nothing Nothing where
merge ma mb =
(case (ma,mb) of
(Just a,Just b) -> put (a,b)
_ -> id) $
get $ \y -> case y of
Left a -> merge (Just a) mb
Right b -> merge ma (Just b)
Input to
f >·< g is split, the first
component is fed into
f, and the second component is fed
into
g. The combined fudget will not output anything
until both
f and
g has output something. After
this has occurred, a message from one of the subfudgets
f
or
g is paired with the last message from the other
subfudget and emitted.
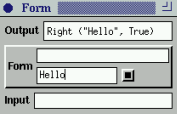
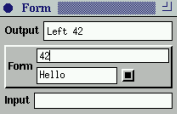
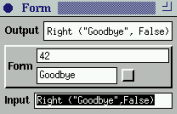
We are ready for a small example. The figure shows a form which
can handle input which either is an integer, or a pair of a
string and a boolean.

myForm :: FormF (Either Int (String,Bool))
myForm = border (labLeftOfF "Form" form)
An extended example connects the input and output of the form
with fudgets to demonstrate the message traffic:
main = fudlogue $
shellF "Form" $
labLeftOfF "Output" (displayF >=^< show)
>==< myForm
>==< labLeftOfF "Input" (read >^=< stringInputF)
This program is illustrated in
Figure 82.
Figure 82. First, the user has entered the string "Hello" and
activated the toggle button. Then, the user entered a
number in the integer form element. The last picture is a
simulation of how the form can be controlled by the
program, in this case by entering a value in the Input
field. The value sets the form and is propagated to the
output.
The little form program is a tangible example of how types can
influence the semantics of a Haskell program through
overloading. To some extent, this style allows a programmer to
freely modify the type of data structures during development
without the need to change the code that deals with the
GUI. Together with the automatic layout system, this provides
(limited) automatic GUI generation. However, as can be seen in
Figure 82, there is much room for improvement of the
form. For example, there is no visual feedback that reveals the
state of a form element of type
Either. It would be
desirable to highlight the part that is valid (or to dim the other
part).
This generation can also be performed for user defined datatypes
by using polytypic programming [JJ97],
based on the instances for products and sums. Polytypic
programming allows us to define how instances should be derived,
based on the structure of the user-defined datatype. For more
complicated (for example recursive) types, it might be a better
idea to base the form elements on the fudgets for structured
graphics in Chapter 27.
After the functionality is there, the programmer's attention might
turn to the look of the forms, and we need a way to tune
them. An approach that immediately comes to mind is to add an
extra attribute parameter to the form method.
class FormElement a t where
form :: a -> FormF t
If we have an instance
FormElement a t, we
can construct a form for a type
t, given an attribute value
of type
a. A problem with this approach is that currently,
only one parameter may be specified in a class declaration in
Haskell. Multi-parameter classes are allowed in Mark Jones' Gofer
[
Jon91], which also allows instance declarations for
compound types like
String. With these features, we could
define instances as follows.
instance (FormElement a t,
FormElement b u) => FormElement (a,b) (Either t u)
where form (a,b) = vBoxF (form a >+< form b)
instance (FormElement a t,
FormElement b u) => FormElement (a,b) (t,u)
where form (a,b) = hBoxF (form a >·< form b)
instance Graphic a => FormElement a String
where form a = labLeftOfF a $ stripInputSP >^^=< stringF
instance Graphic a => FormElement a Int
where form a = labLeftOfF a $ stripInputSP >^^=< intF
instance Graphic a => FormElement a Bool
where form a = toggleButtonF a